1. Home

Patterns and Relationships: Level 4

Thanks for visiting NZMaths.
We are preparing to close this site by the end of August 2024. Maths content is still being migrated onto Tāhūrangi, and we will be progressively making enhancements to Tāhūrangi to improve the findability and presentation of content.
 

For more information visit https://tahurangi.education.govt.nz/updates-to-nzmaths

The key idea of patterns and relationships at level 4 is that rules to describe the relationship between variables can involve multiple operations.

A key development at this level is the generalisation of number properties and the use of algebraic symbols to describe relationships. For example, the distributive property of multiplication over addition can be expressed as the general rule a (e + h) = ae + ah. The use of this property to solve multiplication problems using place value partitioning will be familiar, as in 6 x 13 = 6 x (10 + 3) = 6 x 10 + 6 x 3 = 60 + 18 = 78.

Students will able to describe the relationship between two variables using tables, using words, as an equation, and graphically. In general, straight line relationships are the main focus at level 4. For example, the equation t = 30w – 100 can be used to describe the relationship between the number of weeks saving $30 per week and the total amount saved, when the beginning point is an overdraft of $100. This can be shown in a table and graphically:
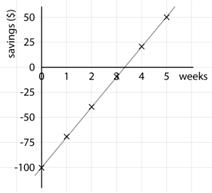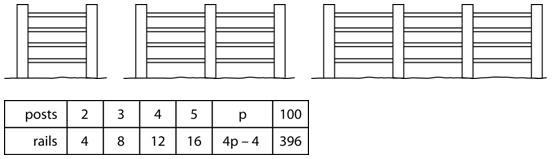
Relationships between variables can be explored using a geometric model as illustrated by the number of posts and rails to build a fence:



This key idea develops from the key idea of patterns and relationships at level 3, focussed on using, representing and generalising patterns and relationships in a variety of ways.

This key idea is extended to the key idea of patterns and relationships at level 5 where the students explore the connections between equations and graphs showing a relationship between variables.