The key idea of patterns and relationships at level 3 is that patterns and relationships can be used, represented and generalised in a variety of ways.
At this level, patterns and relationships form the basis for many of the strategies that students are using to solve number operations. It is important that students are challenged to identify patterns and relationships, and then explore to see if they can be generalised. It is common to show patterns and relationships in tables. The following example shows the pattern generated by the ‘equal addition’ strategy to solve subtraction:
| beginning number | 54 | 55 | 56 | 57 | 58 |
| number being subtracted | 18 | 19 | 20 | 21 | 22 |
| result | 36 | 36 | 36 | 36 | 36 |
Students will use multiplicative strategies to determine the nth term in a repeating pattern. For example, the fourth term in this pattern is yellow and there are 4 elements in the repeating part, so every multiple of 4 (4, 8, 12, 16 ...) will be yellow. One and two less than every multiple of 4 will be blue, and three less will be red:
| term | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 |
| colour | yellow | red | blue | blue | yellow | red | blue | blue | yellow | red |
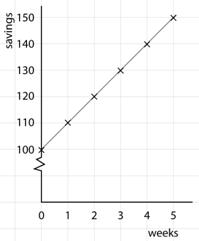
Students will generate patterns and describe relationships between variables arising from everyday situations such as saving a set amount of money each week. The amount saved weekly is multiplied by the number of weeks, and the amount that was in the acount at the beginning is added to get the total. The relationship can be shown in a table and graphically:
 |
 |
This key idea is extended to the key idea of patterns and relationships of level 4 where the students use algebraic equations to show relationsips between variables.
