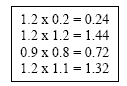Solve multiplication and division problems that involve decimals.
Number Framework Stage 8
10 by 10 grids
Using Material
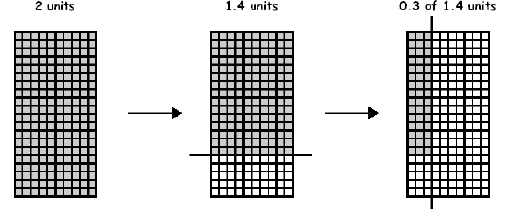
Problem: “John wants to find the area of a rectangle 1.4 by 0.3. Because 1 tenth x 1 tenth = 1 hundredth John decides to make one unit of area equal the square with 100 little squares.”
Get the students to use Material Master 8–34 to draw the following:
Discuss how the pictures show 0.3 of 1.4 = 42 little squares.) (Answer: 3 columns of 14 are shaded in the third picture which gives 3 x 14 = 42 little squares.)
Discuss what fraction of a square unit is shaded. (Answer: 42/100 = 0.42.)
Discuss the quick way of seeing 0.3 x 1.4 = 0.42. (Answer: 3 tenths of 1.4 is less than 1, in fact about 0.5. The answer has 42 in it. So it must be 0.42.)
Examples: Repeat for: 1.6 x 0.2 1.2 x 1.2 0.9 x 0.8 1.2 x 1.1
Using Number Properties
Problem: “John notices a pattern in the answers above. He immediately reasons the answer to 2.5 x 1.3 must be 3.25. Explain.”
(Answer: John notices that ignoring the decimal point 25 x 13 = 325. And 2.5 x 1.3 is between 2 x 1 = 2 and 3 x 2 = 6, so the point must follow the 3.)
Problem: “John’s calculator is malfunctioning. It gives digits in the answer correctly but is not showing the decimal point. He puts 178 ÷ 0.0892 into the calculator and gets 1995515695 on the screen. Where should the decimal point go?”
(Answer: 178 ÷ 0.0892 ≈ 200 ÷ 0.1 = 2 000. So the answer is 1995.51695.)
Examples: Estimate the answer then put the decimal point in the correct place:
9.789 x 0.12 = 117468
10.11 x 9.9 = 100089
4.9 x 0.51 = 2499
78.6 ÷ 0.88 = 893181818
6.76 ÷ 0.026 = 26
2.5 x 2.5 = 625 ...
Understanding Number Properties:
Describe how you would know where the decimal point will be in the answers to a) 234.567 ÷ 24.987 b) 0.0123 x 678.34