This problem solving activity has a measurement focus.
Does a square peg fit better into a round hole or does a round peg fit better into a square hole?
- Draw a diagram to represent a physical situation for a general case.
- Apply Pythagoras’ theorem to a general situation.
- Devise and use problem solving strategies to explore situations mathematically.
Students may be familiar with the phrase "you can't fit a square peg in a round hole".
This problem is a straightforward application of the formulae for the areas of a circle and a square.
The Problem
Does a square peg fit better into a round hole or does a round peg fit better into a square hole?
Teaching Sequence
- Get students to draw both shapes.
- Talk about what a "better fit" might mean. Suggest a relation with percentage of area left over.
- From their visual perceptions ask them to vote.
Square peg in round hole. Circle peg in square hole. Both the same - Students may need to work from a specific radius measurement, for example, 5 cm, if they have difficulty setting up the general case.
- Focus questions that can help students get started include:
How can we set this up?
What information do we know?
How would we label the diagrams?
What mathematical knowledge/formulae could we apply to this situation?
How will we compare the cases? - Encourage students to clearly justify their reasoning by writing a concluding statement to explain their answer.
- Shares answers.
- Reflect back on the original votes. Discuss the difference between visual factors that might make the square look like a better fit.
Solution
Begin by agreeing on a definition for "fits better". This can be connected to the "waste space" after the peg is fitted. This "waste space" is best expressed as a percentage of the larger shape. This is because the answer is then a ratio that is independent of the size of the objects.
Apply this approach to each situation.
Square peg in round hole.
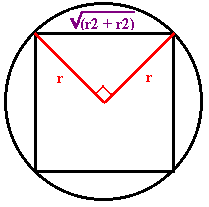
If the radius of the circle is r, then by Pythagoras’ Theorem, the side of the square is √(r2 + r2) = √ (2r2) = r √2.
Hence the area of the square is r √2 x r √2 = √ (2r2) x √ (2r2) = 2r2.
The area of the circle is πr2.
Students could look at the ratio area square/area circle = 2r2/πr2 = 2/π.
As a percentage this is 200/π which is approximately 63.66%.
Round peg in square hole
Alternatively they may then subtract the square area from the circle area to find the wasted area.
2 (π - 2). The percentage wasted is π - 2/ π x 100 = 36.33%
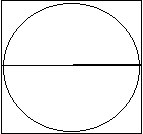
The area of the circle is πr2.
From the diagram, the side length of the square is 2r.
Hence the area of the square is (2r)2 = 4r2.
Students could find the ratio area circle/area square = πr2/4r2 = p/4. As a percentage this is 100π/4 = 78.54%.
The circle covers more of the square than the square does the circle. It’s therefore better to be a round peg in a square hole than a square peg in a round hole.
Alternatively they may then subtract the area of the circle from the square area to find the wasted area.
4 r2 - πr2 = r2 (4 - π). The percentage wasted is then 4 - π/4 = 21.46%.
