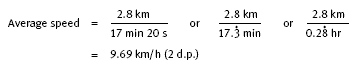Coast to Coast

There are three key skills involved in this activity, all of which need to be specifically taught. They are:
• counting elapsed time
• converting time expressed in minutes and seconds to time expressed as a decimal fraction
• performing calculations with distance, speed, and time.
In the activity, time is expressed in the form 7:45:20. Check that your students understand this notation; it is unlikely to be a problem to those with digital watches.
Counting elapsed time
Although there are algorithmic methods of working out elapsed time by subtraction, the students are unlikely to appreciate what they are doing or why. A better method is to count on to the next whole hour, then on from that hour to the final time, and then to add the two times together to get total elapsed time.
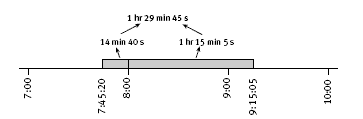
Example: what is the elapsed time from 7:45:20 a.m. to 9:15:05 a.m.?
The time to 8 a.m. (the next whole hour) is 14 minutes and 40 seconds. The time from 8 a.m. is 1 hour, 15 minutes, and 5 seconds. Adding minutes to minutes and seconds to seconds, we get an elapsed time of 1 hour, 29 minutes, and 45 seconds. This can be represented on a time line:

The students should practise adding up amounts of time where the seconds come to more than 60 or the minutes come to more than 60. Most students will know that 72 minutes is 1 hour and 12 minutes, so they should have little trouble with the concept involved.

Converting minutes and seconds to a decimal fraction
A calculator is normally needed to convert time expressed in minutes and seconds to time expressed as a decimal fraction, and the process will require explicit teaching.
The students need to understand that 1 hr 29 min 5 s means 1 hour + 29 minutes + 5 seconds. They also need to understand that 5 seconds is 5/60 of a minute and 29 minutes is 29/60 of an hour:
• on a calculator, 5 seconds is 5/60 = 0.0833 minutes
• 29 minutes 5 seconds is therefore 29 + 0.0833 = 29.0833 minutes
• 29.0833 minutes is 29.0833/60 = 0.4847 hours
• 1 hour, 29 minutes, and 5 seconds is therefore 1 + 0.4847 = 1.4847 hours.
The sequence of operations on the calculator is 5 ÷ 60 [=] + 29 [=] ÷ 60 [=] + 1 =. (The operator in square brackets is not required on many calculators, but it may be safer to encourage the students to use it.)
Distance, speed, and time
All students will bring certain intuitive understandings to a discussion on distance, speed, and time. These should be the starting point for teaching this topic.
Typically, students will understand that:

• if they are travelling at 100 km/h, they will cover 100 kilometres in 1 hour, 200 kilometres in 2 hours, and so on (distance = speed x time);
• if they drive 150 kilometres in 2 hours, they will drive 75 kilometres in 1 hour, so their speed is 75 km/h (speed = distance ÷ time);
• if they have 180 kilometres to travel and they are driving at 90 km/h, it will take them 2 hours to reach their destination (time = distance ÷ speed).
The problem with distance, speed, and time is working out the relationships in a particular problem, and you should encourage the students to go back to first principles like the ones above, rather than apply a formula.
Because the relationships are often inverse, you should expect the students to think about the kind of answer they are looking for. You could ask: “If distance is increased, what will this do to time? If speed is increased, what does this do to time?”
A final consideration is units. Time is measured in hours (and parts of hours), distance is usually measured in kilometres (and parts of kilometres), and speed is usually measured in kilometres per hour. The students need to take care to use the correct units in each situation and to abbreviate them correctly.
In this activity, the students need to solve applied problems involving distance/speed/time from a variety of angles. The students could work out the average speed in question 1 like this:

Calculating Dad’s speed on the first cycling leg (question 2b), we see that he covered 58 kilometres in 2 hours, 14 minutes, and 56 seconds. The first step is to convert the time to hours expressed in decimal terms: 56 seconds is 56/60 = 0.933 minutes, so altogether, we have 14 + 0.933 = 14.933 minutes. Converting this to hours, we have 14.933/60 = 0.2488 hours, so altogether, the time taken is 2 + 0.2488 = 2.2488 hours. Now that we have the time as a decimal, we can use this to calculate average speed.
Speed = distance ÷ time, so speed = 58 ÷ 2.2488 = 25.79 km/h, which is 26 km/h rounded to the nearest kilometre.
In 3e, the average speed for day 1 is found by dividing the total distance travelled by the total time taken. The total distance is 86.8 kilometres and the total time is 7:59:06 or 7.9850 hours. So Dad’s average speed is 86.8 ÷ 7.985 = 10.87 km/h.
Note that this is not the same as finding the average of 9.69, 25.79 and 4.77 (Dad’s speed on each of the three stages), which is 13.42 km/h. The reason we can’t use this approach is that the stages are different lengths.
In question 4, we have the reverse situation in which the resulting time is expressed as a decimal and we need to convert it to hours, minutes, and seconds. Dad covered 15 kilometres at an average speed of 26 km/h, so the time he took is 15 ÷ 26 = 0.5769 hours. This is a bit over half an hour, so we need to be working with minutes: 0.5769 x 60 = 34.62 minutes. This is 34 minutes plus a little over half a minute (0.62), so we
now need to work with seconds: 0.62 x 60 = 37 seconds. So, Dad took 34 minutes and 37 seconds to cycle from Klondyke Corner to Mount White Bridge.
Cross-curricular links
Achievement Objectives
After they have done some research on the Coast to Coast race, you could put the students in pairs and ask them to create a crisis scenario that might occur during the race. They then write an account of the crisis, describing the scenario and what organisation was required by people (organisers and participants) to resolve it.
Social Studies
Demonstrate knowledge and understandings of:
• how people organise themselves in response to challenge and crisis (Social Organisation, level 4)
• how and why people exercise their rights and meet their responsibilities (Social Organisation, level 4)
Health and Physical Education
• specify individual responsibilities and take collective action for the care and safety of other people in their school and in the wider community (Healthy Communities and Environments, level 4)

Answers to Activity

1. 9.69 km/h
2. a. 2 hrs 14 min 56 s
b. 26 km/h (rounded from 25.79)
3. a. 86.8 km
b. 5 hrs 26 min 50 s
c. 5 km/h (rounded from 4.77)
d. He was running over uneven terrain with a lot of uphill and downhill work. Also, this was the final stage in a gruelling day.
e. 10.9 km/h
4. 8:04:37 a.m.
5. 5 hrs 35 min
6. 1:39:37 p.m.
7. a. 2 hrs 58 min 50 s
b. 24 km/h (rounded from 23.5)
c. 238.8 km
d. 17 hr 7 min 33 s
Investigation
Answers will vary.