This is a level 5 number activity from the Figure It Out series. It relates to Stage 8 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (1144 KB)
sovle problems involving ratios
Number Framework Links
Use this activity to help students learn to solve problems involving fractions, proportions, and ratios (stage 8).
This activity introduces ratio in an enlargement context. Students learn that by comparing known lengths, they can find missing lengths. They also learn how to test whether one figure is an enlargement of another.
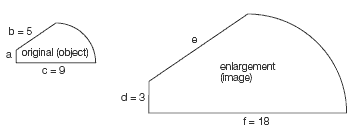
The key idea behind enlargement is that all lengths grow or shrink according to the same ratio (or scale factor). If they didn’t, the figure would lose its shape. If we put any length from an enlarged figure over its corresponding (matching) length in the original figure, we get the number (often a fraction) known as the scale factor. This principle can be described mathematically as image/object = scale factor.
When two figures are related by enlargement, as in the example above, we can use ratio in two different ways:
1. To compare a length in the enlargement with its corresponding length in the original. These comparisons are made between figures and can be thought of as external comparisons. Any such comparison will give the scale factor for that enlargement.
In the figure above, f/c = d/a = e/b = scale factor. f/c = 18/9= 2, so the scale factor is 2. This means that all lengths in the enlargement are twice what they are in the original. We can use this information to show that a = 1.5 and e = 10.
2. To compare the relationship between two lengths within the enlargement with the relationship between the two corresponding lengths within the original. These comparisons can be thought of as internal comparisons. In the figure above, f/d = 18/3 = 6. This means that the base of this figure is 6 times height d. The same must be true of c and a in the original. We can use this information to show that height a is 1.5 (1/6 x 9). In addition to f/d = c/a, other comparisons can be made, including d/e = a/b and e/f = b/c. These ratios are all different, and none equals the scale factor. You can’t find the scale factor by comparing the lengths of sides within the same figure – only by making comparisons between figures.
Some problems can be solved using either of these two kinds of comparison (for example, question 1); most require one or the other (for example, question 2).
The above ideas are included for teachers who are uncertain about the application of ratios to enlargement. There is no need to teach them formally at this level. Focus instead on building on intuitive understandings about enlargement and applying them to simple contexts with easy numbers, as in this activity.
In question 1, students can use ratio in either of the two ways outlined above:
1. By comparing the base of the small rectangle with that of the medium rectangle, it can be seen that the scale factor must be 4/6 = 2/3. In other words, all lengths in the small rectangle are of what they are in the medium rectangle. This means that height A must be 2/3 x 9 = 6 cm. Similarly, by comparing the base of the large rectangle with the base of the medium rectangle, we can see that the scale factor for this enlargement is 20/6 = 10/6 = 3 1/3. So height B must be 3 1/3 x 9 = 27 + 3 = 30 cm.
2. Comparing the height of the medium rectangle with its base, it can be seen that the height:base ratio is 9/6 = 3/2 = 1 1/2. In other words, the height is 1 1/2 times the base. The same must be true in the small rectangle, so height A must be 1 1/2 x 4 = 6 cm. Similarly, height B must be 1 1/2 x 20 = 30 cm.
Students may need help to understand what question 2 means and to realise that they have to find which pairs of pictures have the same height:width or width:height ratio. Encourage your students to find their own strategies for solving this problem and to share them. The simplest strategy is likely to be to express each ratio in its simplest form (either using ratio notation, as below, or as a fraction):
i. 4:6 = 2:3
ii. 9:15 = 3:5
iii. 5:6 = 5:6
v. 12.5:15 = 25:30 = 5:6
vi. 6:9 = 2:3.
From the above, it is obvious that i and vi both have the same width:height ratio, as do iii and v, so these must be the pairs.
Answers to Activities
1. a. 6 cm. (Compare bases: the base of the smallest picture is 4/6 = 2/3 of the base of the medium picture. This means that height A will be 2/3 of the height of the medium picture. 2/3 x 9 = 6 cm.)
b. 30 cm. (Compare bases: the base of the largest picture is 20/6 = 10/3 = 3 1/3 times the base of the medium picture. This means that height B must be 3 1/3 x 9 = 30 cm.)
2. i. and vi.
iii. and v.