Session One

In this exploration students attend to situations where angles are present. In doing so, they recognise that these situations can be dynamic, e.g.an ice skater turning, or static, e.g. a playground slide.

1. Begin by showing students Slides One through Five of PowerPoint 1.
   In each of these pictures there is an angle. Tell me where you can see angles. Have a korero with a partner and share your ideas.
2. Through examples, try to develop a working definition of an angle. Pictures present a static view of angle. That view is useful in construction but it neglects the important relationship that connects all angles, the turn or rotation.
3. Show the students Slide Six which rotates a ray (one-directional arrow) in relation to another.
   Where is the angle in this picture?
4. Students may attend to the point where the rays intersect. That is an important feature of an angle. They may attend to the space between the rays which is a distractor. On clicks of the mouse the ray rotates further.
   Is the angle staying the same, getting smaller, or getting bigger?
   What is causing the angle to get bigger?
   Students usually agree that the angle is increasing in size though they may be attending to area, and not to rotation. It is also important that students realise that an angle can be greater than a right angle. You might mention the right angle when the rotation reaches 90⁰. 
   What are the important features of an angle?
   Students should mention the intersection (important), the rays (rather than lines), and the turn, which is the relationship between the two rays.
5. Slide Seven contains pictures of scissors of various sizes. Ask the students to discuss in pairs or threes:
   Which pair of scissors is the most open?
6. After a suitable time, bring the class together to discuss the pairs of scissors. Use Slides Eight and Nine to highlight that it is the rotation, rather than the area, between the rays that defines the size of the angle. Slide Ten shows the two most open pairs of scissors. The two angles can be compared using the right angle as a benchmark. The black handled pair is open at more than 90⁰ and the green handled pair at slightly less than a right angle.
   Some students might suggest measuring the angles with a protractor. The animation shows how to do that (use mouse clicks to navigate). 
   You are now going to learn a bit about how people learned to measure angles based on the Babylonian method from many years ago.
7. Provide students with Copymaster 1 and ask them to work through the problems. Encourage sharing of their thinking and collaboration (mahi tahi) with others. Look for students to make connections between the base of 360 degrees (as in days of the year) and the fractions they need to create. Some students may need a calculator for division but encourage the use of mental strategies, where possible.
8. After students have completed the tasks work through the remaining slides of PowerPoint One. Look to see that they can estimate benchmark angles such as 90⁰, 45⁰, and 60⁰. Are they able to adjust their noticing to accommodate the changes in orientation?

Session Two

1. Begin the lesson with Copymaster 2. In this activity students estimate the size of given angles first then check their estimates with a protractor. The difference between estimate and actual angle is calculated. At the end students can sum their differences and compare their performance with those of classmates.
2. Next, show the students a video of a goal kicker from rugby, rugby league, AFL (Australian rules), or football (soccer). All the sports have female professional leagues so be gender inclusive.
   If the commentator said that a player scored from an acute angle, what would that mean?
   Are there kicking positions that are harder to score from than others? Why?
3. You might ask students to draw diagrams to explain their thinking. The difficulty of a kick can be due to several variables including distance, wind direction, preferred foot of the kicker, nature of the ball, and angle. Focus on angle, assuming distance and other factors are controlled.
   Let’s imagine the kick is only 20 metres from goal. 
   Which position gives you the best chance of kicking the goal? Why?
4. Students might create a scale drawing of the situation using 1cm grid paper.  A scale of 1cm=5m or 1cm=2.5m works well. Alternatively draw the situation like this.
   
   As the kicker moves further away from the central point the angle gets smaller, making the shot more difficult. In real games, a kicker taking a kick from a non-central position, moves further back to increase their angle.
5. Take the class outside. You will need to take clipboards and paper, a large blackboard protractor, PE cones or markers, and a long builders’ rope (cheap at hardware stores). Place the markers at different angles to the posts at a distance such as 10 metres which is easily kickable. Measure the angles using the rope and the protractor.
   
6. Station a record keeper at each marker and several balls (rugby, soccer, tennis balls can be thrown if necessary). Station half the class as ball receivers on the other side.
7. Let each student have two or three kicks from each station (Kickers and receivers will need to change places). Record keepers keep tallies of the successful and unsuccessful shots.
8. After the kicking is complete bring the class inside to look at the data.

9. Create a table like this:

   Angle	Successful	Unsuccessful
   15⁰	13	45
   24⁰	21	37
   36⁰	36	22
   55⁰	45	13

10. Ask the students to use calculators to change the numbers to percentages. For example, 36/58 = 36÷58 = 62.1%.
    What do you notice about the success rate as the angle changes?
    Naturally the success rate declines as the angle declines. Likewise, success rate increases as angle increases.
11. Use Copymaster 3 as practice of applying angles to goal kicking.
12. Students could investigate angles in sports or games they are familiar with. For example, running between pou in kī-o-rahi, making a pass across the field in hockey, or shooting from a certain position in basketball.

Session Three

In this lesson students play two games related to angles, snooker and golf. Look up short videos of both sports online, and briefly discuss how angles are involved in each game.

1. Use PowerPoint 2 to discuss two things:
   • The path of a ball after it hits the cushion (side of the table).
   • The path of a ball when it is hit by another ball.
2. Slides One to Three show billiard balls bouncing off cushions. Ask students to look at the first path of the ball and anticipate the direction the ball will bounce off the cushion. Protractors appear to show how the angle of entry and departure are related.
3. Slides Four to Six show situations where the cue ball hits a target ball. In general, a line from the pocket through the centre of the target ball tells where to aim the cue ball (assuming no spin). After impact the cue ball travels at a normal (right angle) to the line. The slides also include bounces off the cushion which students should be encouraged to anticipate.
4. Ask students to estimate the angles for all three slides then reveal the protractors to check. You may need to discuss obtuse angles that measure between 90° and 180°.
5. Copymaster 4 has some scenarios for students to explore. They will need a pencil, ruler and protractor. As your students work look for:
   • Do they recognise that the entry angle must equal the departure angle?
   • Do they orient the protractor, and read the angles properly, to mark the departure path?
   • Do they recognise that alternative paths off the cushion are parallel?
   • Do they notice that the angle of the cue ball after impact is normal (at right angles) to the line for the pocket to the target ball?
6. The golf game is designed to practise angles from 0° to 360° as bearings. To find a bearing measure the angle clockwise from due North. For example, a bearing of 135° is shown below. Note that a bearing is used to face a particular direction, and is used in navigation and orienteering.
   
   Students need to combine their estimates of a bearing and distance to play each shot. Slide Seven shows an example of a hole being played. Provide the students with Copymaster 5, a protractor and ruler. Let them play a round of golf!

Session Four

In this final lesson students apply their knowledge of angles to create a logo with rotational symmetry.

1. Slides One to Three of PowerPoint 3 show how an element can be rotated to form a logo. The number of rotations of the element before it returns to starting position is called the order of rotational symmetry. The angle of rotation is the result of equally partitioning 360⁰ by the order. For example, to create a logo with rotational symmetry of order four, the element is rotated four times through an angle of 360⁰ ÷ 4 = 90⁰.
2. After viewing the first three slides, move to complete logos on Slides Four to Six. Discuss how to work out the order of rotational symmetry for each logo, and how the angle through which the logo maps onto itself.
3. Students can then work on Copymaster 6 which requires them to identify the rotational symmetry of complete logos.
4. After students have completed the task ask them to design their own logo using rotational symmetry. The completed logos can be given to other students for analysis. Students may wish to use digital technologies, such as PowerPoint, Scratch, or Geogebra to create their logos.

Getting Started

In this first session, the students investigate rectangles on dot paper but through the context of the rectangles that two students (Jess and Hannah) have made.  Allow your class to collaborate in pairs as this helps to stimulate discussion, and supports students to clarify their ideas and resolve any problems.

1. Pose the following problem:
   Jess and Hannah are trying to solve a problem. They draw these shapes. Show PowerPoint 1.
   What is the problem they are trying to solve?
    
2. Focus the discussion on similarities and differences among the three shapes. Expect ideas like:
   • They are all rectangles (What defines a rectangle? Four sides and four right angles).
   • They are different sizes (How do you describe the size of a rectangle? Length by height)
   • They have different perimeters (What is perimeter? Distance around the outside of the shape)
   • By the end of the discussion your students should identify that the areas are the same (24 square units).
      
3. Slide 2 of PowerPoint 1 shows how the square units tesselate to fill the rectangles with no gaps or overlaps (click to animate). Discuss how multiplication can be used to find the area and what the factors refer to.
   For example, the area of the rectangle that has eight rows of three squares can be found using 8 x 3 = 24 or 3 x 8 = 24 (length x height is the usual convention).
    
4. Challenge the students to complete the problem that Jess and Hannah are solving:
   How many different rectangles can be made that have an area of 24 square units?
   Give students copies of the square dot paper.
    
5. After an appropriate time, bring the class together to share solutions. Slide 3 has all the possible rectangles and illustrates a systematic way to find them. It also shows that 4 x 6 is the same rectangle as 6 x 4 as one maps onto the other by rotation of a quarter turn.
    
6. Ask the class to use the dot paper to draw all the different rectangular shapes that have an area of 36 square units?  (Note: Some students may realise that they do not have to draw all the shapes to identify which ones will have an area of 36.) Do they also realise that a 6 x 6 square is a type of rectangle?
    

7. With the students construct a table which records the different rectangular shapes:

   Rows	Columns	Area
   1	36	36
   2	18
   3	12
   4
   5
   6
   9
   12
   18
   36

8. Have students complete the table and explain how their system of recording indicates all the different shapes that can be made that have an area of 36 square units. They could share with a partner, and then to the class.
   Do you notice the point at which the rectangles are repeated?
   For example, 3 x 12 is the same rectangle as 12 x 3.
   What is the relationship between 6 and 36? (since 6 x 6 is the last discrete rectangle before repeating occurs).
   Six is the square root of 36 (√36 = 6)
   What do you think square root means?
9. Ask the students to use a table to find all the different rectangles that have an area of 64 square units.
    
10. From the work that you have done so far, write a rule that would allow you to quickly find the area (in square units) of any labelled rectangular shape.
    What is the area of these rectangles? (See PowerPoint 1 – slide 4)
    A mathematician might write the area rule like this:
    a = l x h
    What does the rule mean? What does each letter, a, l and h refer to?
     
11. Give students the following problem:
    A rectangle has an area of 72 square units.
    It has a length that is twice its height.
    Draw the rectangle.
    
    Students might make up a rectangle area problem like that for a classmate to solve.

Exploring

This section is divided into two parts. In Session A students discover the relation between the area of a parallelogram or trapezium and the area of a rectangle. In Session B, the area of any triangle is connected to a ‘surrounding’ parallelogram.

Session A

1. Ask the students to draw a unit square (1 x 1) on their dot paper. Tell the students that each side of the square is said to have unit length and that the area is one square unit.
   If the distance between each dot is 1 centimetre, what would you call the square? (1 square centimetre).
   How do we write one square centimetre? (1 cm2)
   If the distance between each dot is 1 metre, what would you call the square? (1 square metre)
   How do we write one square metre? (1 m2)
   You might like to show the actual size of the one square metre using 4 one-metre rulers.
   (The aim of this task is to allow students to develop techniques that will help them to analyse the mathematical situations that they will meet in the rest of the unit.)
    
2. Make a rectangle using cardboard strips and split pins.
   Show by pushing the edges a little that you get a parallelogram.
   
   What do we call shapes like this? (Parallelogram.)
   What does a quadrilateral need to have to be called a parallelogram? (Two pairs of parallel opposite sides)
   You may need to use the metaphor of railway tracks to illustrate the meaning of parallel.
   Which is bigger, the area of the rectangle we started with or the area of the parallelograms as we pushed?
   What would happen to the area if we pushed the rectangle right over?
   Why would it have no area?
    
3. Jess and Hannah wondered how they could find the area of any parallelogram. They reasoned that parallelograms must be related to rectangles when the heights are the same.
   Why do Jess and Hannah think the heights must be the same? (As the rectangle was pushed, the height decreased, and the area decreased as well.)
   Let’s start with a parallelogram. Can we turn it into a rectangle? How?
   Show the first slide of PowerPoint 2. Let your students visualise how the parallelogram might be ‘cut and pasted’ to form a rectangle.
   If you click on the mouse an animation will show the transformation.
   Why do the two shapes have the same area? (The area of both triangles is the same)
   Can you transform a rectangle into a parallelogram?
   Show slide 2 and ask students to visualise cutting a triangle off the rectangle and translating it to the other end.
    
4. Give students a copy of page 1 of Copymaster 1. Ask them to cut out each parallelogram and transform it into a rectangle, then calculate the area. Look for students to recognise that area remains invariant (does not change) as the triangle that is removed from one end is added to the other end.
    
5. Gather the class to discuss a rule for finding the area of a parallelogram. If necessary, show why the area of a parallelogram can be found from a rectangle with the same length and height. This relies on the fact that the two end triangles in the diagram have the same area (triangles ABC, A’B’C’). This is easily shown by drawing a diagram and cutting out the triangles. One will fit over the top of the other. This shows that the parallelogram AA’B’B has the same area as the rectangle AA’C’C. An internet search for “parallelogram to rectangle gif” shows numerous short animations of this action. 
   
   The length and the height are needed to find the area of a parallelogram. Therefore:
   area = length x height.
   
   An important point to note is that height is measured using a line that is at right angles to the base.
6. Challenge your students with this problem:
   
   Draw three different parallelograms that have an area of 60 square units.
   The parallelograms must have the same length.
   
   Or
   
   Draw three parallelograms with the same height that have an area of 60 square units.
   
   Could your answers to both questions be the same? Why?
   
   Look for students to notice that ‘tilting’ the base rectangle but keeping the height the same conserves area.
    
7. Ask the students to identify a connection between the areas of rectangles and trapezia. A trapezium has one pair of parallel sides.
   Page two of Copymaster 1 provides many trapezia. By cutting out each trapezium, then cutting along the dotted lines, students can rearrange the pieces to form a rectangle.
   How are the side lengths of the original trapezium and the rectangle connected?
   
   In general, any trapezium can be transformed into a rectangle by cutting and pasting. The length of the rectangle is the average of the two different lengths of the original trapezium. The height remains the same. 
   

Session B

1. Jess and Hannah wondered if the area of triangles is related to the area of parallelograms and rectangles.  They investigated the area of right-angled triangles first – triangles with one right angle.
    
2. Slide 1 shows an animation of how the two triangles might be put together.
   How are the areas of the triangle and rectangle related?
   Your students should note that the triangle is half the area of the rectangle.
   How could we write a rule for the area of a right-angled triangle?
   Record the rule as words or symbols, whatever the students come up with.
    
3. Jess and Hannah realised that most triangles are not right-angled. They investigated the areas of other triangles.
   Copymaster 2 provides two copies of different triangles. Ask your students to cut out the similar (same shape) triangles and put them together to make a quadrilateral.
   What kind of quadrilateral is formed each time?
   How is the area of the quadrilateral related to the area of the triangle?
   
   Students should notice that a parallelogram can be formed each time. Slides 2 and 3  of PowerPoint 3 illustrate how one triangle can be joined to the other by a half turn and a translation (shift). Focus attention on the connection between the length and height of the parallelogram and the original triangle.
    
4. Ask the students to write a short paragraph using pictures, to illustrate how to find the area of any triangle. Their work should include a formula (in words will do) for the area. (Area = half the base x height.) For example, the area of the triangle below is ½ x 9 x 7 = 31½.
   

Reflecting

Here the students use the formulae that they have obtained earlier to solve some problems.

Problem 1

Get the students to choose one of the shapes below, draw it on dot paper and find its area. The students can choose their own dimensions for the shapes. This can be done in at least two ways. By cutting it up into rectangles and by counting squares on the dot paper.

Problem 2

This problem could be adapted to suit the context of your learners. Instead of making a vegetable garden, students may be more interested in designing a rectangular classroom or playground. Consider what your students have recently been learning about, and are interested in, and try to make links to these areas.

You have been given 36 metres of string to ‘rope off’ a rectangular area that can be made in to a vegetable garden. What is the largest rectangular garden you can make?
Justify your choice, using diagrams and or tables of information.

Lesson One: Exploring bullying statistics in New Zealand

In this unit students explore some statistics about bullying in New Zealand schools.

TIMSS 2014/15 and PISA 2015

1. There are several online articles about bullying available if you want students to search for information. However, a very brief summary is provided in PowerPoint 1. Show the first three slides of the PowerPoint.
   Stop after slide three and discuss these questions with your students:
   • Do the findings surprise you?
   • Do the findings match your experience at school?
2. Some students might perceive bullying to be only physical violence. Broaden the idea of bullying by asking:
   What kinds of behaviours (things people do) might be bullying?
3. Make a list of bullying behaviours then look at Slide 4. Copymaster 1 is a bigger copy of the graph for students to use.
4. Ask students to look at the graph and interrogate it. Get them to discuss the graph, in small groups, and record their thinking about how the data about bullying may have been gathered.
   How did the people who created this graph gather their data?
5. Encourage the students to research online, a search for "TIMSS 2014/15" should lead to the Education Counts report. The Ministry of Education report He Whakaaro: What do we know about bullying behaviours in New Zealand? (Mhuru, 2021) contains TIMSS key facts which are useful to interrogate the data provided in the graph. Some interrogative questions to use to support student thinking are:
   • Who was surveyed?
   • Who did the surveying?
   • When was the questionnaire completed?
   • Who is the graph of? How do we know?
   • What data is the graph showing?
   • Which survey question was used to provide the data in the graph?
     • Hint: look at year 5 student and year 9 student survey questionnaire for TIMSS
     • For 15-year-olds use the 2018 PISA report (search for "PISA 2018 New Zealand students' wellbeing" to find the PDF document)
     • Bullying information from PISA is in the wellbeing report from page 20 on.
6. Rove around to see what students are thinking. Encourage them to be specific. In particular:
   • Do they discuss asking a group (sample) of people?
   • Who do they select? (School aged children at ages 9, 13 and 15 years)
   • How many people do they select? (Sample size)
   • What do they ask the people they select? (Specific response examples)
7. Gather the class and discuss the points above. The sample sizes in TIMSS and PISA are very large, e.g. over 8,000 students in TIMSS 2014/15. You might ask what a practical sample size might be for a small study. Students might highlight that asking a small number of people may not give reliable results. Why not? (variability)
   Why couldn’t we ask a very large number of people? (Only so many students in our school, too much time, hard to process all the data)
8. Once you have interrogated the graph and understand what data was collected, from who, and how it was collected, start to discuss the findings.
9. Ask your students what they notice about the graph. Use the starter “I notice…” on the board and get students to work in small groups to notice everything they can. This may also require them to go back to the data source to see more about where the data came from. 
   Look for the following capabilities in your students:
   • Do they recognise that the triple bars refer to data from different age groups?
   • Do they notice that the percentages of students reporting bullying are higher for younger students than older students? [Why might that be? – see page 28 of the PISA report]
   • Do they notice that the length of specific bars provides a percentage?
   • Can they read off specific percentages?
   • Do they know what percentage means? (A rate of x in every hundred students)
   • Can they classify the bullying behaviours? [e.g. physical, verbal, emotional, etc.]
   • Do they notice that posting embarrassing things about me online is only for year 9 students, why? [year 9 questionnaire was the only one that asked about that]
   • Why are there no 15-year olds in the “somebody shared embarrassing information about me” or “I was made to do things I didn’t want to do” categories? [these were not in the PISA questionnaire]

Extra bullying data to explore if needed for the lesson

If there is time in the lesson, the 2015 CensusAtSchool questionnaire had four questions on bullying. Data from these questions were shared with the media in the form of press releases. More recent questionnaires have not included questions on bullying. However, it could be worth looking at CensusAtSchool questionnaires for other data to use with your class.

On 12 June 2015 CensusAtSchool made a press release with the heading: Verbal abuse the biggest bullying problem at school: Students.  

Subsequently Radio New Zealand, Maori Television, NZ Herald, and Stuff (twice) published their own articles based on the CensusAtSchool press release. See links to all articles here.

Students can read the original press release and then in groups pick one of the other press articles and compare the press articles with the original press release. Ask the students what they think they should compare. E.g. is the data used in the article the same as the press release, what additional reporting has been included, is it relevant to the topic?

Copymaster 2 has nine graphs made from a sample of 1000 students from the CensusAtSchool 2015 database. See if these graphs support the evidence in the original press release.

You can make your own graphs by downloading a sample from the CensusAtSchool data viewer. Agree to the conditions of use; in the plan section select the CensusAtSchool NZ 2015 database, for the total sample size put 1000. Then select get data. This results in the Analysis section coming up, and therefore the option for graphing. Select the variable(s) to investigate, then select "do analysis". Students can do additional analyses by repeating the process - select a variable, then select "do analysis". The graphs stack up on the screen.

Introducing the PROBLEM

Today we have explored existing data on bullying in New Zealand in preparation to undertake our own statistical investigations on bullying. This will be our topic to investigate. Over the next few lessons we will explore developing a questionnaire, collecting and analysing data and reporting our findings.

Lesson Two: Understanding survey questions

In this second lesson we will explore existing survey questions on bullying to help us to see the structure of survey questions and to consider good ethical practices for collecting data, especially for potentially sensitive topics. We will look at the different types of survey questions that might be asked.

1. Show the students slides five to seven of PowerPoint 1. The survey questions shown are taken from publicly available surveys about bullying. For each survey question, ask students about what is found out from the survey question.
   Why might the investigators want that information?
   The main purpose is to extend students’ ideas about what might be asked about bullying, from establishing its occurrence (what, when and where), to finding out actions that students take, and ideas about how the situation might be improved, if it needs to be.
2. Copymaster 3 has the three slides on one page for students to answer. Hand out the sheet and ask students to think about their possible responses to the survey questions. They are not to answer the survey questions, just think about their possible responses. Once this is done, ask the students to discuss in their groups if any of the survey questions would be hard to answer, by themselves or by others, and why, and whether there are any issues with the wording of any of the survey questions. Groups to make notes to report back to the class. 
   Note for teachers: Students are not asked to complete this questionnaire on paper, in class, for ethical reasons. Two key ethical practices that potentially would be violated are:
   • minimising the risk of harm to participants
   • respecting and protecting participants’ privacy and confidentiality
3. Feedback may include: 
   • The ethnicity survey question requires a student to opt for one ethnicity when some may identify themselves with two or more ethnicities, e.g. The child of a Thai mother and Samoan father. This survey question assumes students will identify with only one ethnic group “the most”. This is not a good assumption.
   • The open response survey question, about why no action was taken, might imply blame. That can lead to students not answering honestly. When people respond to survey questions either by providing incorrect information or by answering untruthfully this is called a response bias and is an example of a non-sampling error.
   • Students may indicate that one or more of the survey questions made them feel uncomfortable or that they did not want to answer them. They probably will not want to explain why, but point out to them that when they get to develop their own survey questions they need to think about this when they write their own survey questions – they should ask themselves if others would feel comfortable answering the survey question.

CensusAtSchool 2015

The 2015 questionnaire for CensusAtSchool had four questions on bullying.  

In preparation for completing the online questionnaire teachers were provided with a PowerPoint to support their students with the sensitive topic.  Show your students the PowerPoint 2 presentation, including the introduction to CensusAtSchool.

The first three slides set up the purpose for CensusAtSchool and talk about participating in the census. Understanding the purpose of a survey is important for those who choose to participate.

The next three slides discuss the bullying survey questions. The slides allow the teacher to introduce the topic of bullying, definitions of bullying, the idea of getting consistent responses for the survey and where to go for support.

Share the four questions on bullying from the 2015 CensusAtSchool survey (Copymaster 4).  Ask the students to think about how they would respond to these survey questions and then to discuss how they would feel about answering these survey questions?  How are these survey questions about bullying different to the ones we looked at earlier? How are they similar?

These are all ideas that can inform the students developing their own survey questions about bullying.

Collecting demographic data

In the next lesson students will develop survey questions about bullying. One of the areas to think about is what demographic data should be collected.

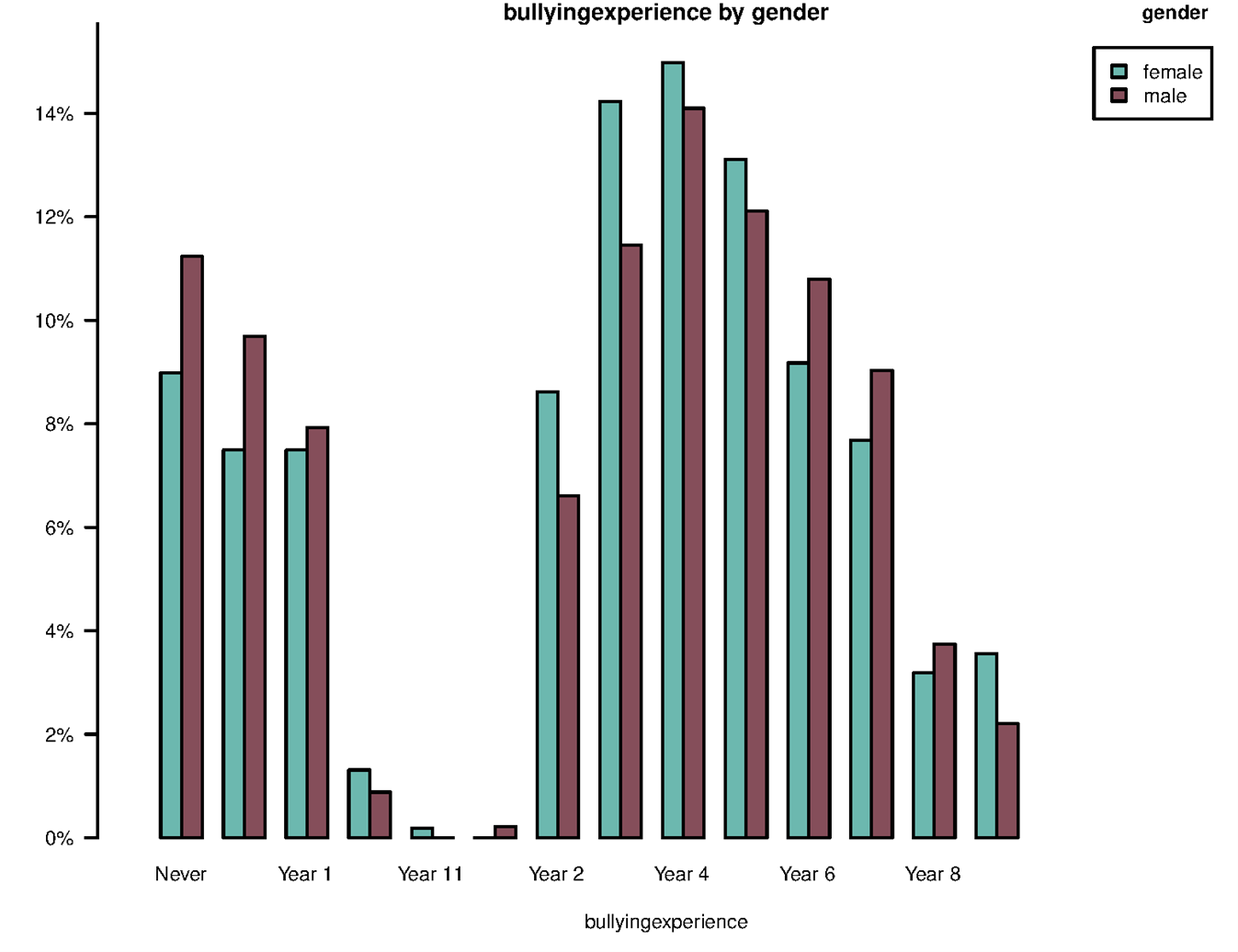
Demographic data includes data about ethnicity, gender, location, education, class level, position in family etc. Demographic data is often used to split the data into groups to compare. For example, two of the graphs (Graphs 6 and 9) from the CensusAtSchool survey (Copymaster 2) on bullying show the data compared by gender. Graph 6 is also shown below.

What personal information should be found out about the students?

Students might suggest the usual demographic variables such as age, class level, gender, and ethnicity. They may suggest other variables of interest, such as position in the family, e.g. first born, middle child, youngest child.

Ask the students if we should ask for people’s names and why or why not? Hopefully, they will say no and make links to confidentiality and validity (i.e. people might not answer honestly if they can be identified).

It is good to also ask about other demographic data that they have suggested.

Which of these might also identify people too easily, even if we do not have people's names?

Suggestions could include ethnicity, especially if there is only one child of a certain ethnic group in a class, and even ethnicity with gender – a single girl or boy of one ethnicity.

Lesson Three: PLANNING to collect data to answer investigative question(s)

Remind students that the topic we are investigating is bullying. We will develop survey questions to explore the topic in this lesson. To investigate the topic we need to think about the areas of bullying that we could target.

Share with the students that bullying surveys usually include sections of survey questions. The sections are based on what the investigators want to find out. Common themes are:

1. Types of bullying and frequency (What and how often?)
2. Location and timing (Where and when?)
3. Responses to bullying by students (How do they react?)
4. Knowledge of help to counter bullying (Who/Where to go to? What can you do to help?)
5. Effects of bullying on the well-being of victims (What are the effects?)
6. Rationale for bullying (Why do students think bullies bully?)
7. Improvements (How can the school improve?)

Reflect on previous survey questions from lesson two and identify which of these themes the survey questions are about.

Developing survey questions on bullying

Ask your students to choose four themes and write one or two survey questions for each one. Suggest limited response survey questions rather than open survey questions to keep data handling manageable. Handling of open response data is dealt with later. You may want to discuss PowerPoint 3 which shows the three most common types of closed survey questions. Focus on the advantages and disadvantages of closed survey questions.

• Advantages: Short time for respondents to complete, data is easy to code and interpret, allows use of numbers (quantitative methods).
• Disadvantages: Respondents are forced to select an answer they do not totally agree with, reasons why they answer as they do are not available.

Let your students work in teams of three to develop survey questions. Preferably they should do so digitally so the survey questions can be edited, and combined with others, to form the final survey. Provide feedback as you go around.

Will the survey questions provide important data?
Are the survey questions simply, and briefly written?
Are the words and phrases unambiguous?
Does each survey question include only one idea, not multiple ideas?
Are the survey questions neutral, avoid leading statements, and offer a full range of options for students to choose?

About ethics:

Is the survey question one that students at our school would be happy to answer?

Are the survey questions sensitive to different cultural and religious perspectives?

Before sharing survey questions with the class, ask the students to trial each survey question with at least two other students who are not in their team. The survey questions should be rewritten if needed.

Share a few of the survey questions with the whole class. Focus on the above criteria for good survey questions. Organise the survey questions under the seven themes above.

Defining our investigative questions

Our next task is to develop a questionnaire to answer our investigative questions. First though we need to define our investigative questions we want to answer.

Reflecting on all the exploration and development work we have done to date, pose 2-3 investigative questions that we can answer through collecting data about bullying. The themes we have looked at previously will help you with this. [For more on posing investigative questions see Travel to school]

Creating a questionnaire to answer our investigative questions

Display all the survey questions that were developed under the theme headings. Students develop a bullying questionnaire in teams of three. Set the restriction that the survey must:

• Ask three demographic survey questions (Name is not included – Why?)
• Address four themes
• Ask two or three survey questions per theme
• Include survey questions that will help to answer their investigative questions

Have the class pool of survey questions stored digitally on an accessible drive so that students can cut and paste to form their questionnaires. It is a good idea to introduce checking once the questionnaires are drafted. Each group can check to see that the questionnaire of another group is sound.

Once the questionnaires are checked and completed these should be entered into an online survey tool, such as Google Forms or SurveyMonkey. Be aware that some platforms often incur a charge. Two advantages of digital platforms are that the data is entered by respondents, and the data is downloadable as a spreadsheet. 

Prepare for the surveys to be completed by other classes. Think about the ethics of data collection as a class and which of these are important in the invitation we send and the information we give to the classes that will complete our surveys for us. The main ideas to discuss here are:

• obtaining informed and voluntary consent from participants
• respecting participant’s right to withdraw at any time without giving a reason
• respecting and protecting participants’ privacy and confidentiality
• avoiding any unnecessary deception to participants

These ideas can also inform an introduction to the survey which outlines things such as the survey is anonymous, no names are collected, and no identifying information is asked.

Lesson Four: Collecting DATA and ANALYSING data

1. Get each group to gather data from another class in the school using their survey.  This will probably involve going to the class, a brief introduction to the purpose of the survey and then being available during the survey to answer any questions.
2. Students could also survey a class from another location if you have a reciprocal arrangement. The advantage of reciprocal arrangements is that your students will experience first-hand being a respondent to a survey. That will make them sensitive to the importance of clear survey question construction, and the time taken to respond.
3. Once the students from other classes have completed the survey, students can process their data. While processing can be done manually there are advantages to using statistical software e.g. CODAP or similar, in terms of display and calculating statistics. For more on using CODAP see Travel to School and Planning for a statistical investigation Level 3.

Lesson Five: CONCLUSION – answering the investigative question and reporting our findings

In the final reflection part of the unit students are required to report their findings about bullying. They are also encouraged to think about their process of investigation and what they have learned from it.

1. Provide time for your students to construct a report that shows the results of the investigation. Copymaster 5 could be provided electronically as a .docx or copied into a google doc so that students can write into it, and import data displays they have created.
2. Invite different groups to share their findings. Accept the fact that a non-finding, such as little bullying is reported, is a legitimate result. Where bullying is reported, look for students to connect the variables as well as reporting on the results of individual questions. For example, there might be a connection between type of bullying and location or time that the bullying occurs, e.g. social bullying occurs most in the playground at play and lunch times. Also encourage the students to make recommendations about how the school can apply and use anti-bullying strategies, such as educating students about how to respond to bullying, and being aware of the most vulnerable students.
3. The class might compile a report for the principal or Board of Trustees detailing the findings and recommendations. Any report should respect the confidentiality of the students who responded so that details about individuals, and classes, remain confidential. Links could also be made to persuasive and informative purposes for writing.
4. If time permits you might like to investigate how to deal with data from open response questions. PowerPoint 4 has an example of an open response question, and a fictitious set of examples of students’ answers. Coding of open responses generally proceeds in two ways:
   1. A set of categories is established beforehand based on expectations, preferably informed from reading.
   2. Builds categories as they become needed.
5. Ask your students to read the comments on Slide Two.
   Are there things in common about the comments? How could we group them?
6. Students might suggest sensible ways to classify the comments. Alternatively, click the mouse so that the comments appear in different colours.
   How have the comments been grouped?
7. Challenge students to describe the categories. They might suggest:
   • Yellow: Student’s behaviour encourages bullying
   • Green: Racial discrimination
   • Blue: Physical disability
   • Pink: Family circumstances
   • Purple: Learning disability
8. If any groups have collected open response data that might be used as an example where students can practise coding data.

Session One

1. Arrange five cardboard packets of similar volume but different appearance on a desktop. 
   What is the same about the shape of all these packets?
   Students will spot many commonalities that are all valid, e.g. made of cardboard, shaped like rectangles, six faces, etc. Focus the students’ attention on the shape features the boxes have in common. All five boxes are composed of six rectangles.
   Is there a mathematical name for boxes of this shape?
   Students may know that all the boxes are rectangular prisms, sometimes called cuboids. Look up the definition of a prism online. Something like this will be returned:
   A prism is a polyhedron, with two parallel faces called bases. The other faces are always parallelograms. The prism is named by the shape of its base.
2. Relate the definition to the packets on the desktop. 
   What does parallel mean? Where are the two parallel faces? (Look for two identical [congruent] faces at opposite ends)
   What is a parallelogram? (Quadrilateral with two pairs of parallel opposite sides)
3. Ask your students to draw three different parallelograms. Try to broaden their view of what shapes are types of parallelograms, including the rhombus, rectangle and square.
   
4. Look at Slide One of PowerPoint 1.
   Discuss which of these solids is a type of prism.
   Look for students to identify congruent ‘end’ faces (can be base and top) and parallelograms, usually rectangles, wrapping around the sides of the end faces. Prisms are named by the end faces. Slide one has a triangular prism. A cylinder can be classified as a type of prism, though it is the limiting case with an infinite number of rectangular faces.
   Also consider the non-examples. Slide One has two pyramids (triangular and cone), curved surfaces (sphere), and some other polyhedra (octahedron and icosahedron).
5. Discuss why this shape is not a prism. (The end faces are not congruent)
   
6. Come back to the boxes on the desktop. 
   Your task is to find out the largest number of little cubes each of your five boxes will hold. Label the boxes so you can refer to them.
7. Show the students a single 1cm³ place value block cube.
   What can you tell me about the size of this cube?
   You may need to measure the edges of the cube with a ruler to convince them that it is a cubic centimetre. Show them how the unit size can be written as 1 cm³, and said as “one cubic centimetre”.
   We write the size of this cube as 1cm³. What does the ‘3’ represent? (the cube is 1cm in all three dimensions, length, height, depth)
8. Set the students to work in small groups. Each group needs five different packets, a ruler, a calculator, one single place value block cube, and paper to record their working. Ensure students support each other and have opportunities to experience both tuakana and teina roles as they do this. Look for your students to:
   • Recognise that the cubes need to be packed tightly to get the largest number in each packet.
   • Find more efficient ways to count the number of cubes, e.g. create a layer or stack.
   • Measure the edge length to save iterating the unit cube along edges.
   • Use multiplication of edge lengths to find the volume of each box in cubic centimetres.
   • Apply fraction knowledge to find the volume of parts where the cubes do not fit exactly, i.e. vacant space.
9. After an appropriate time, gather the class to have a korero about their strategies. Choose groups that illustrate a progression in sophistication:
   Fill and count → Create stacks → Create layers → Multiply whole number edge lengths
10. Ask students to explain their methods rather than focus on specific answers. You might use Slides Two, Three and Four to discuss how multiplication works to calculate the volume of a rectangular prism. An interesting point of discussion is whether the order of multiplying matters. For Slide Four:
    Does 8 x (5 x 5) give the same volume as 5 x (8 x 5)?
11. Copymaster 1 has some volume problems for students to solve. As students work check to see how they are calculating each volume:
    • Is multiplication their preferred method?
    • Can they combine multiplication and division to find the missing side lengths?
12. Talk with students about the world’s tallest buildings, or the tallest buildings in your local area. While the more recent tall buildings, like the Auckland Skytower, are in thin cylindrical-shaped tower form, some of the older structures are combinations of cuboid shapes. For example, the Sears Tower in Chicago, and the Rialto Tower in Melbourne, are collections of cuboid in structure. Pictures of these buildings are easily found online.
13. Tell the students that they are to make a scale model of a tall building by glueing together at least three different cardboard packets from those brought to school. Each building is then glued to a base to form a skyscraper, as seen in large cities throughout the world.
14. Allow students time to develop their skyscrapers in groups of four or five. Bring the class back together and discuss what statistics could be displayed about each building. Suggestions might include height, width, length, and volume. Discuss whether naming the dimensions correctly matters (i.e. height, width, length, depth, breadth, etc). Which is which? Does it matter? When naming the dimensions of a three-dimensional figure, the most important thing to remember is make sense and be clear. It is helpful to use labels. To demonstrate this, you could model writing down the different dimensions of a real building from an image (some estimation or research may be required), or focus on the dimensions of one of the scale models. 
    Invite suggestions about how the volume, in cubic centimetres, might be worked out. Ideas might include building a cuboid of similar size and counting the cubes (successful but inefficient), making one layer of the building, counting the cubes in one layer and using equal additions to make up the height of the building, and multiplying by the edge lengths. Highlight the efficiency of the edge length approach.
15. Send the students away to label their structures, with stickers in appropriate places, giving the name of the building (eg. The Toa Tower), and the various edge lengths in centimetres. Note that for some packets these lengths may need to be rounded to the nearest centimetre. Monitor the students’ accuracy in measuring to the nearest centimetre.
16. When each building is labelled, instruct the students to choose any five buildings from around the room and calculate the volume (office space) of each structure in cubic centimetres. After a time the original creator of each building can calculate its volume and display it using a sticker. Each student can then compare their solutions and discuss discrepancies with the builder.
17. The class tries to identify the room’s biggest buildings by height and volume. This data could be displayed in a graph as an extension and a suitable scale (eg. 1cm = 10 m) established to relate the models to their actual size in real life. Note that the scale has interesting implications for volume in cubic metres. A scale of 1cm = 10m will mean that 1 cm³ = 1000 m³ which is a very large space.

Session Two

In this session students attempt “The cereal box challenge”. Their task is to maximise the volume of a cereal box that can be made from A4 sized pieces of 1cm grid paper. You could adapt the learning in this session to reflect the current learning, and/or cultural makeup of your class. For example, instead of a “cereal box challenge” you could pose the problem as designing a pattern for a Wakahuia or Papahou (wooden containers used to hold personal taonga, or treasures).

1. Begin with the packets that were used in Session One. 
   Cardboard packaging is usually created by die cutting a template or net, creasing the template, then folding up the packet. Tabs are glued to hold the packet together. You might find a video online to illustrate the creation of packaging (search “How cardboard boxes are made”).
   Sketch what you think the template of your packet would look like before folding and glueing. Be as accurate as you can. You will need to measure the edge lengths of the packet and draw the template the correct size.
2. Provide pairs of students with a packet, blank A3 sized paper, cellotape, rulers, pencil, and scissors. Let them attempt to recreate the template. Look for students to:
   • Use some ‘prototypical’ template for rectangular prism (usually a t shape).
   • Accurately measure the lengths of the edges of the packet.
   • Transfer the measurements to the correct place on their template.
   • Provide tabs in appropriate places and part faces where those parts form the top and bottom of the packet.
3. Once students have created a template, they can cut it out, fold it, and tape it. Ask them to compare their template to the original packet, and notice any ways they could improve it. 
   Does the packet give volume information?
   Most packets provide information about net weight, that is the mass of the contents. This can be quite misleading as often the contents are nowhere as much, by volume, as the packet.
   Why do the manufacturers only provide weight information?
   Most contents in packets compress as they settle from the time they were filled. This is particularly true when the packets are transported. Net weight does not change though volume does.
4. Introduce the challenge using PowerPoint 2. Let students work on pairs to create the box they believe maximises the volume. You might pair students up for increased support, and encourage tuakana-teina, or work with a small group of students to model this activity. Students will need copies of Copymaster 2, rulers, scissors, tapes, and calculators. Look to see if students:
   • Minimise the wastage from pieces that are not in the box template.
   • Consider how changes to their template increase or decrease the volume.
   • Experiment with lengths that are fractions and decimals, e.g. 7.5 cm.
   • Recognise that a cuboid as close as possible to a cube is likely to have maximum volume.
5. It is important that students record edge lengths on their template, and take a digital photograph as a record before the template is folded and taped. Students can record the volume of their box inside it so the finished products can be ordered by volume.
6. After an appropriate time, gather the class to compare the boxes that have been made. 
   What were some considerations as you found the box with the greatest volume?  
   Students should discuss how changing an edge affects the length of other edges. They should also acknowledge the constraint of the 19cm x 28cm size of the paper, and how increasing the height of the box decreased the base, and vice versa. You might put three pairs of students together to check the volume calculations (call that volume auditing).
7. Display the boxes by stapling them to a wall, possibly in order of volume. A winning entry might look like this box that has a volume of 7 x 7 x 6 = 294 cm³.
   
   Some students might also consider the normal shape of a one-serve cereal box and opt for a less regular shape.

Session Three

In this session the problem is based on finding the most efficient way to pack a collection of cuboids (rectangular prisms) into a confined space. This skill has many real-life contexts that you may wish to use as a story shell, including packing the car boot for a holiday or groceries at the supermarket. The context of the NASA first space trip to Mars may create more interest. Space is at a premium on spacecraft and advanced technology is designed to be compact!

1. Provide the students with connecting cubes of various colours, they will need their 30cm ruler as well. Instruct them to build the following packets from the cubes. Make each packet a different colour. Note that connecting cubes are 2cm x 2cm x 2cm.
   • 4 cm x 4 cm x 6 cm
   • 2 cm x 8 cm x 6 cm
   • 6 cm x 6 cm x 4 cm
   • 2 cm x 6 cm x 4 cm
2. Their task as the NASA engineer is to find a way of putting the parcels together in the most compact way possible. Allow the students time to attempt the problem. Stress (i) the need to record their solutions and (ii) that they should not join the packets together so that they can be unpacked if they haven’t been joined together correctly. Arranging the packets by manipulation is quite easy.
3. Ask the students to work out the total number of cubes used. This creates an interesting crosscheck where the number of cubes in the combined cuboid can be checked against the sum of the cubes in the four packets. Ask the students how knowing the total volume of the combined cuboid could help in arranging the packages in a more difficult problem of this type. In this example the total volume is 48 connecting cubes (384 cm³) so that limits the dimensions of the cuboid (e.g. 4 x 6 x 2, 3 x 4 x 4).
4. Challenge:
   Tell the students to:
   • Choose one of the packets they used in Session One. It must have edges that are whole numbers of centimetres and be as big as possible.
   • Make up a set of up to six cuboids, using different colours, that will fit exactly inside the packet they have chosen.
   • Record a solution to their problem in some way. Isometric drawing is a good method (see Copymaster 3). Students could explore isometric drawing in more detail using the Little Boxes activity if necessary. 
   • Give their problem to another group of students to solve.
5. After the students have attempted a few problems, gather the class to have a korero about possible strategies. Many students will use trial and error approaches, but some may be more systematic. Did they:
   • Record the dimensions of each cuboid multiplicatively, e.g. 2 x 3 x 4.
   • Measure the box and calculate the total number of connecting cubes needed.
   • Compare the edge lengths with the dimensions of each cuboid. (This can eliminate or confirm the locations of some cuboids)
6. The final problem is about a growing cuboid pattern. Give the students Copymaster 4. Calculators will be needed as the volumes get quite large. You might get a few students to build the cuboids so they can be referred to.

7. Students are likely to begin by calculating the volumes of the first three buildings and arranging the data in a table:

   Building	1	2	3
   Volume	6	24	60

8. They are unlikely to make much progress by looking at differences in the table. Instead they should focus on what changes as the pattern increases. Each dimension increases by one and depth is always the pattern number. Width is one more than the pattern number, and height is two more. In general, the volume can be calculated as n x (n + 1) x (n + 2), where n is the pattern number.
9. The final question can be attempted by trial and improvement. However, it is more efficient to consider that n x n x n will be a bit less than 7890. N x n x n is the same as ‘n cubed’ so students could use a scientific calculator, e.g. 20³ = 20 x 20 x 20 = 8 000. Therefore, n must be a little less than 20. 19 x 20 x 21 = 7890 so n is 19, meaning 7890 is the volume of the 19th building.

Session Four

Problem One:

1. Show the students Slide One of PowerPoint 3. 
   What does ‘L’ mean when referring to a backpack or chilly bin?
   Students may be familiar with L referring to the unit of capacity, the litre.
   Surely that does not mean that the backpack is going to be filled with water. Why is the litre used as the unit?
   The use of litre means that the measure is referring to the capacity of the backpack or chilly bin. Capacity is how much a container holds and usually refers to amounts of liquid or gas.
2. Hold up a 1 litre milk carton.
   This is a one litre container. Estimate how many cubic centimetres are equivalent to one litre.
3. Let your students estimate then measure the dimensions of the cuboid section of the one litre carton. The dimensions are usually; height (22cm), length (7cm), depth (7cm). Since 7 x 7 x 49 = 1078 cm³ which include air space. The actual volume of one litre is 1000 cm³.
4. Present a set of place value blocks.
   Who can make up the volume of one litre?
   Students should recognise that gathering 1000 unit cube will be tiresome, and collect bigger units, such as flats that represent 100cm³. Ten flats have a combined volume of 1000cm³ and form a cube that is 10cm x 10cm x 10cm. If you have a large place value block cube that represents 1000cm³ you might present it then.
5. The capacity of a backpack is the volume when it is completely full. Your task now is to work out the capacity of your school bag in litres. 
   Students will need rulers and calculators to work out the capacity of their school bag. Encourage them to record their calculations so that it can be verified. After a suitable time, gather the class to discuss what they found out.
   What is the average bag capacity for students in our class?

Problem Two:

1. Pose this problem (see Slide Two of PowerPoint 3).
   The Just Juice Company wants a new carton that will hold exactly 330 mL of juice. Each edge of the new carton must be an exact number of centimetres long (e.g. it cannot be 4.75 cm long).
   One possible carton would be 330 cm x 1 cm x 1 cm. Ask the students to imagine what that would look like and how we know it would hold 330mL. Suggest that this carton would not be very practical and invite them to design other cartons which are more appropriate.
2. The students can make their cartons from centimetre squared paper if needed but encourage them to use their knowledge of volume to solve the problem efficiently. Issues such as the ease of fit in a person’s hand should be considered.

3. Allow the students time to find several possible cartons and bring the class together to share their ideas. Focus on their use of the cuboid volume formula (width x breadth x height) and the application of factors in finding workable dimensions. For example, if 10 cm is to be the length of one edge then 330 ÷ 10 = 33 gives the product of the other two edge lengths. Therefore 10 x 3 x 11 are the dimensions of one possible carton. The possible carton sizes could be entered in a table, in a systematic way, to check if all possible cartons have been found. Spreadsheet formulae could be used to make calculations easier:

   Edge One (cm)	Edge Two (cm)	Edge Three (cm)	Volume (cm3)
   1	1	330	330
   1	2	165	330
   1	3	110	330
   1	5	66	330
   1	6	55	330
   1	10	33	330
   1	11	30	330
   1	15	22	330
   2	3	55	330
   2	5	33	330
   2	11	15	330
   3	5	22	330
   3	10	11	330
   5	11	6	330

4. Decide as a class on the most suitable dimensions. You might compare the class solution to actual dimensions of a small juice carton.

Other possible extension problems:

1. What different cuboids can be made with a volume of 180 connecting cubes?
   Which of those cuboids is most compact? Explain why.
    
2. Make a cuboid from connecting cubes that has dimensions of 2 x 3 x 4.
   Now make the cuboid that has each dimension doubled, that is, 4 x 6 x 8.
   When the edges are doubled in length what is the effect on volume?
   How does volume increase if you treble or quadruple edge length?
   Investigate, and explain why this happens.

Prior Experience

This unit is targeted at Level 4 so students are expected to have experience at Level 3 including:

• Creating tables and graphs for simple relations
• Knowledge of common graphs for category and numeric data, e.g. stem and leaf, bar graph
• Measurement with metric units
• Simple percentages

Session One

In this session students investigate some of the mathematics of astronomy associated with the rising of Matariki. They learn to recognise the cluster of stars irrespective of orientation. They also learn where to look for the stars at the beginning of Matariki and how the date of the New Year is determined.

Use PowerPoint 1 to organise the lesson.

1. Slide 1: Why is the star cluster Matariki important in Aotearoa/New Zealand at this time?
   Matariki is a cluster that wanders the skies in relation to other star formations. For eleven months of the year it is visible as it wanders. In early May it disappears below the horizon and reappears close to the horizon in late May/Early June. The ‘rising of Matariki’ refers to its appearance above the horizon just before dawn. That is why it was used as a consistent marker to determine the New Year. So the first new moon following the ‘rising of Matariki’ is when the New Year begins, but celebrations occur in the last quarter of the lunar cycle before.
2. Slide 2: How will you recognise Matariki when you see it?
   There are seven stars in the cluster visible to the naked eye, though another two stars can be seen by some with keen eyesight or with binoculars. As a cluster, the seven stars stay in the same formation like a squadron of stunt pilots. However, the cluster appears facing different directions at different times which can make it hard to spot.
3. Give the students Copymaster 1 which includes the star cluster in different orientations. Ask the students to find a way to know if the cluster they see is Matariki. After all, there are billions of stars in the sky.
4. When they return, ask the students what methods they use to organise the way they view the cluster. Typically this involves using shapes, relative position and size of the stars are important characteristics. You might put the students in small groups to share their organisations with the aim of creating the easiest way to recognise Matariki. Get the students to apply their organisations to Slides 3-6.
5. Slide 3: This is Matariki rotated 120° (⅓ turn) clockwise from the arrangement on Slide 2. A good question is why the Slide 2 position is easy to recognise. For example, the two right hand stars Tupu-ā-rangi and Tupu-ā-nuku are aligned vertically. Students will have other reasons.
6. Slide 4: This is Matariki rotated 210° clockwise or 150° anti-clockwise. An important discussion point is the similarity of effect for these two rotations.
7. Slide 5: This is not Matariki as the relative location of Waitā has been changed (moved to the right). If the students have used shapes to organise the cluster then the shift will be obvious.
8. Slide 6: This is a reflection of Matariki so is not how the cluster can appear. Discuss why a reflection (flip) is not a valid transformation while a rotation is.
9. Slide 7: This shows one way to organise Matariki using a rhombus and an isosceles triangles. Share the other ways students used to organise the cluster geometrically. Mention that using figures to describe the arrangement of star clusters is common across cultures.
10. Slide 8: Here you will find instructions about locating Matariki in the sky as it rises an hour or so prior to dawn in the North-Eastern sky. Give your students a Google Map of your local area so they can identify some landmarks to look for to identify East and North-East or let them use the app if you have technology available.
11. Celebrations for Matariki, the New Year, occur after, but not on, the day of the first New Moon after the rising of Matariki in the dawn sky (Late May/Early June). Find out what date Matariki is celebrated this year. You may want to use TimeAndDate.com to help.
    The site will show the quarters of the lunar cycle like this:
    
12. Ask the students, “How many days are in a lunar month?” A lunar month is 29.5 days (New moon to new moon) so it does not match the calendar months of 28-31 days we use. Ask, “So how long does each quarter take?” (About 7 days)
13. You might ask your students to act out the rotation of the moon around the Earth, using a ball and an OHP projector or torch. Acting out the rotation will show if your students understand why the phases of the moon occur. There are videos available online that also demonstrate this. Search for "Phases of the moon video".
14. Ask the students to find the date of the first full moon in June. You might ask students to find the dates of Matariki for the next few years. TimeAndDate.com is a useful resource for this.
15. Ask: Is there a pattern to the dates? Why do the dates vary when the date of Matariki rising is consistent? (The lunar calendar has a different month to the calendar we use).
    You might ask the students to graph the relations, preferably using Excel or another app. The graph reveals a cycle like this that might predict future and previous dates for Matariki. The lines in this graph show the cycle even though the points are discrete (individual). The cycle is erratic, unlike a tide timetable or the pattern of seasons, because the timing of Matariki is dependent on two different patterns. The star cluster varies in the date it first rises each year, and the lunar cycle of 29.5 days does not match our calendar months.
    

Session Two

In this session students investigate the significance of Matariki as a time of remembering ancestors. Ask students to choose an ancestor of their own who has passed in the last year or select a famous New Zealander from an online database. They look at data about the deceased, particularly the nature of the contribution the ancestor has made to the lives of others.

1. Play the section from 31:57 to 35:24 in this inspiring lecture by Dr Rangi Mātāmua about Matariki.
   Dr Mātāmua shows how the star Matariki is at the bow of the great canoe Te Waka o Rangi. The rising of Matariki signals a time of letting go of the dead from the year before so their souls can be gathered in the trawling net by Taramainuku who casts them into the heavens. In that way our ancestors become stars.
2. Begin with the Figure It Out task “Family Trees” from Figure It Out, Link, Number, Book Four, Family Trees, page 13.
3. Use PowerPoint 2 to organise the remainder of the lesson.
4. Slide 1: Ask, “What is this diagram about?” Some students may know that it shows some of the children of Ranginui and Papatūānuku, the first Māori ancestors. Ask, “What is meant by whakapapa? Why is whakapapa important?”
5. Slide 2: This is a picture of Tāne Mahuta, the giant kauri tree in the Waipoua Forest, in Northland (Tai Tokerau). It is named after one of the children, Tāne-mahuta, God of the forest.
6. Slide 3: Ask, “What does this picture show?” The diagram shows a bloodline going backwards in generations from a single offspring.
   Ask, “Why does it say biological whakapapa?” Children do not always live with their parents and sometimes adults find new partners. So the problem has been simplified. Some children have brothers and sisters, and cousins. Great Aunts and Uncles are also referred to as tīpuna.
7. Tell the students to work in small groups to solve the problem on slide 3. Purposeful groupings, that include a mix of abilities and mathematical confidence levels, may be crucial in this task. Students are expected to work with large numbers. Allow them access to calculators and computer spreadsheets if necessary. Look for your students to organise the calculations. A table like this is useful, and could be provided to students as a graphic organiser. Encourage students to use formulae rather than repeatedly copying sequences. You may need to explicitly model how to use formulae. Some examples of formulae that can be filled down are shown. Formulae allow students to fill down the table for as many generations as they want.
   
   So the total number of ancestors in a biological whakapapa is 1023 after ten generations.
8. Ask: Is the second column of numbers familiar? What set of numbers is that?
   These numbers are powers of two and can be written in index notation, e.g. 32 = 25. Note that 2⁵ can be written as 2 x 2 x 2 x 2 x 2 (two multiplied by itself five times).
9. Ask: Is there a quick way to find the value of Column C if you know the value of Column D? 
   Students might notice that the Column C numbers are one less than double Column B, e.g. 1023 = 2 x 512 – 1.
10. The final question asks how many biological whakapapa make up the 100 Billion stars in the Milky Way. Students might interpret this in at least two ways:
    • How many generations down the table would it take to reach 100 000 000 000?
      The result is surprising as it only takes only 37 generations to get 137,438,953,471 ancestors. Note that you will need to custom format the cells to take large numbers before you fill down the table columns. If each generation is 25 years apart then there are 4 generations in each century.
    • How many centuries equal 37 generations? (37 ÷ 4 = 9.25)
    • How many whakapapa of 1023 would make 100 000 000 000?
      ​1023 is about 1000 so 100 000 000 000 ÷ 1023 ≈ 100 000 000 (one hundred million)
11. Remind the students that Matariki is a time to acknowledge the dead prior to the beginning of the New Year. According to custom, as their names are read out at dawn the souls of the deceased are cast into the heavens to become stars.
12. Invite the students to choose a deceased person to acknowledge. The person might be a member of their whānau, someone they knew, or a famous New Zealander who passed recently.
13. Allow students to develop a short acknowledgement of the person, researching on the web if they need to. That acknowledgement should include the contribution the person made, their gender, their location, and possibly their age of death. You might choose to undertake a data based investigation. Students could create data cards about their person for easy sorting:
    
14. Ask: How might we group the reasons we chose our people?
    Students should create categories like family, sport, arts, leadership, business, education, to sort the people into. The person might belong in several categories. For example, Henare might have been a politician as well as a leader.
15. As a class you might create data displays and look for patterns in the data.
    • We tend to value our whānau and sports people most.
    • Most of our people lived beyond 60 years.
16. To conclude the lesson, show the students the story of the creation of sky and earth, beautifully told by Beth Te Aro (see YouTube links below). According to the legend Tāwhirimātea, God of Wind, was so angered by the actions of his siblings that he pulled out his eyes and threw them into the heavens. Another version says that he threw his tears. His eyes or tears formed the stars of Matariki. For this reason Matariki translates to “The eyes of God” or “Little eyes.”
    • Ranginui and Papatuanuku - part one (YouTube)
    • Ranginui and Papatuanuku - part two (YouTube)

Session Three

In this session students follow the connection of Matariki as a time to honour the dead and the responsibility of the living to strive for excellence. Matariki occurs in the middle of winter. Traditionally this was a time when adequate food was stored and whānau engaged in cultural pursuits like story-telling, games, creating art works, and singing. So it is appropriate for students to learn about the mathematics of tukutuku panels that adorn the wall of wharenui (meeting houses) of marae. Students look at a traditional design called kaokao. Toothpicks could be for students to communicate and refine their thinking around patterns and rules. Use PowerPoint 3 to organise the lesson.

1. Slide 1: This kaokao pattern symbolises the strength of the warrior.
2. Slide 2: This slide introduces the two components of some tukutuku:These two components form the variables in the pattern when you consider it from an algebraic perspective. The kaokao pattern has reflective symmetry which can also help students to solve the difficult challenges that lie ahead.
   • horizontal wooden rods or laths, usually coloured red or black, called kaho;
   • cross stitches, made from a variety of coloured fibres, called tuinga.
3. Slide 3: This slide introduces the task, completion of which will enable your students to increase their knowledge. Provide students with Copymaster 2 so they can draw over the pattern in an effort to find an easy way to calculate the number of tuinga.
4. Once the task is introduced, allow students to work collaboratively in small groups. Look for these things as your students work:
   • Do they partition the kaokao into useful ‘chunks’ that mean one-by-one counting is not needed?
   • Do they use tables to organise the data they get about the pattern? Consider providing a table template for students to use.
     
   • Do they notice patterns in the table?, e.g. Four more tuinga are added for each kaho
   • Do they use equations to record the way they partition the kaokao into ‘chunks’? , e.g. 3 x 4 + 2 tuinga for 5 kaho. This will draw on students’ understanding of the order of operations (BEDMAS) and may require additional explicit teaching and modelling.
5. Your ākonga (students) are likely to need a significant time to investigate the pattern. Encourage them to find different ways to ‘see’ the kaokao, that is partition it into useful ‘chunks’. After an appropriate time, bring your ākonga together to share strategies they used to solve the problem.
6. Look at sophistication and efficiency. A strategy that involves adding fours may work for 18 kaho but it will be very cumbersome for 100 kaho. A multiplicative strategy like, “I take two off the number of kaho, multiply that by four then add two”, is much more efficient. A student who invents that would be further up the kaokao than a student who adds. Encourage your ākonga to connect their symbolic recording to the ‘chunks’ they ‘see’. Here is an example, for the multiplicative rule above:
   
7. Ask students who are presenting to use tables to organise the data. Rather than using recursive (additive) rules encourage them to look for direct (multiplicative) rules as shown below.
   
8. You might choose to record the general rules in words or equations, such as:
   "Take two off the number of kaho, multiply the answer by four, then add two” can be written as , where t is the number of tuinga and a is the number of kaho.
9. Slides 4-7 are aimed at your ākonga ‘seeing’ the kaokao in different ways to create different general rules. These ways of seeing may have already been used by your students.
10. Slide 4: Whetu notices groupings of two. She could record:
    
11. Her challenge is to write the multiplier of two in terms of the kaho number. Notice that 3 is the 2nd odd number, 5 is the 3rd odd number, 7 is the 4th odd number. So for 18 kaho she would find the 17th odd number and multiply that number by two. The 17th odd number is 33 so the number of tuinga is 33 x 2 = 66. She could write her formula as 2[2k-3]=t since 2k-3 gives the k-1th odd number. This formula is quite complex but some ākonga may find it.
12. Slide 5: Rawiri sees a collection of six tuinga at the start of the kaokao with three kaho. He notices that four tuinga are added for each new kaho. For 18 kaho he will know that 18 – 3 = 15 sets of four tuinga will be added to the original six. So he would calculate 15 x 4 + 6 = 66. In general, the rule is “Take three off the number of kaho, multiply the answer by four then add six” or 4(k-3)+6=t.
13. Slide 6: Anikiwa sees two halves to the kaokao and she joins the halves together. She notices that two tuinga overlap. If she created a table for each half of the kaokao it would look like this:
    
14. If she doubles each ‘half’ (for left and right) and remembers to take off the overlapping two tuinga she will get this table.
    
    In general her rule is, “Take one of the kaho number and multiply it by two. Multiply that answer by two then subtract two” or 2[2(k-1)]-2=t.
15. Slide 7: Kahu notices that there are three lots of four in the kaokao for five kaho. So he adds tuinga so there are five lines of four. Five multiplied by four is easy to calculate (5 x 4 = 20) then he takes away the six tuinga he added.
    For 18 kaho Kahu will make 18 x 4 = 72 tuinga, then subtract six to get 66 tuinga. In general his rule is “Multiply the kaho number by four then subtract six” or 4k-6=t.
16. Slide 8: The final slide for the lesson gives your ākonga a chance to apply their ‘ways of seeing’ to a new kaokao pattern. In general there are six tuinga per kaho except for the four tuinga that are attached to the top two. You might ask your students to work on this task independently before sharing with others.

Session Four

Matariki was traditionally a time when kites were flown. Some iwi believe that flying kites helps us to get closer to our ancestors whose souls are embodied as stars in the sky. In previous times kites were made from everyday materials, toetoe, raupō and harakeke (flax).

This YouTube video shows examples of traditional manu tukutuku (kites):

• Keeping Kites Flying - Tales from Te Papa episode 115 (YouTube)

1. Ask: How do you think the kites were constructed from natural materials?
2. Toetoe formed the skeleton or frame of the kite, raupō leaves formed the sail, and flax was used to tie the parts together, and as the line. Often kites were made in the shape of birds. These kites were ‘delta kites’ as they were based on a single triangle (tapatoru). Plans for making a delta kite can be found in Copymaster 3.
3. If natural materials are hard to come by then it is still appropriate to use recycled materials in keeping with the environmental focus of Matariki. The sails can be made from materials such as vinyl wall paper or tough plastic rubbish bags. Bamboo garden stakes, long skewers, or lengths of dowel make good spines and struts for the skeleton. Traditionally Māori used supplejack for framing their kites.
4. The size of manu tukutuku (kite) that your ākonga might make is constrained by two things, the size of the rectangle of material and the length of the rods that will form the frame. For example, bamboo skewers are 30cm long and will fit along the side labelled 75%. Longer lengths of dowel or bamboo up to 150cm might also be used. So the size of the sail and keel will need to be adjusted accordingly which is an excellent opportunity to apply percentages. This is an excellent application of proportional reasoning. If 30cm skewers are used, 75% is about three-quarters so 100% must be 1⅓ of 30cm which is about 40cm. Many of the measurements can be estimated accurately, e.g. 10% is one tenth.  If you are using 30cm skewers the measurements become:
   
5. All measurements can be scaled for a larger manu tukutuku. Ask the students to sketch the dimensions of their plans on paper before they cut out the materials. Get other students to check their calculations. 
6. Traditionally kites were flown on the morning of the new moon. You might like to organise a dawn viewing of Matariki and a kite flying regatta to welcome the arrival of new stars in the heavens.