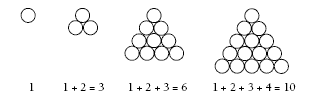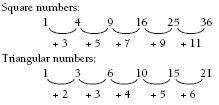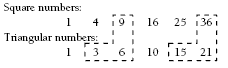Puzzling Patterns

Activity One

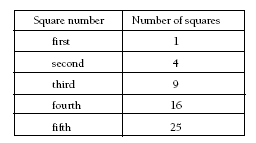
Students can build on their geometry knowledge to find a quick way to count the number of small squares and predict the tenth square number. When calculating the area of a square, students will know that they multiply the height by the width. They can use the same method to calculate the number of small squares in each larger square. They will notice here that the height and the width are the same, that is, a square number is the result of one number being multiplied by itself. They
should also notice that:

• the first square number is 1 x 1 = 1
• the second square number is 2 x 2 = 4
• the third square number is 3 x 3 = 9.

If they extend this pattern, they can predict that the tenth square number will be 10 x 10 = 100.
If students have difficulty grasping these calculations, they could model the shapes with counters or multilink cubes or use a table to record the square numbers:

From the table, they can use the pattern of differences to predict the tenth square number or they may notice that (as explained above) the first square number is 1 x 1, etc. However, encourage students to use calculation because it is a far more efficient method.
The building pattern of the squares in question 2 is not as easy to recognise or calculate immediately. However, students could notice that:

• If they start counting the squares in each building, the totals are the same as the square numbers above.
• The squares to the right of the tallest column can be moved to the left side of the building to complete a square shape.

They can then use the same methods as they used in question 1 to calculate the number of small squares in the tenth building.

Activity Two

If students have trouble seeing why 10 is a triangular number, you could draw smaller triangular numbers, such as three and six, in the same configuration.

The answers explain the patterns of triangular numbers.

Activity Three

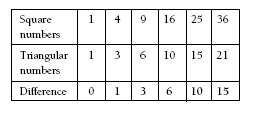
The patterns in the differences between the terms in each set of numbers are illustrated in the answers.

Answers to Activities

Activity One
1. 100
Working: 10 x 10 = 100
2. 100
3. The answer is the same for the tenth object in each pattern. The number of squares is the same for both patterns, even though they are arranged differently. Each part of both patterns is a square number.
Activity Two
1. Ten identical objects can be arranged in a triangular shape.
2. a. Answers will vary. The first picture could be used to find 1, 3, 6, 10, 15, and 21. Adding on layers would give 28, 36, 45, etc.
b. Answers will vary, but one way of looking at the pattern is:
1 = 1
3 = 1 + 2
6 = 1 + 2 + 3
10 = 1 + 2 + 3 + 4
15 = 1 + 2 + 3 + 4 + 5
This can be explained as:
First triangular number: 1
Second triangular number: first triangular number + 2 = 3
Third triangular number: second triangular number + 3 = 6
Fourth triangular number: third triangular number + 4 = 10, and so on.
3. Answers will vary. One explanation is: We know that we can arrange numbers such as 3, 6, 10, and 15 so that they are a triangular shape. If you take the bottom layer off each triangular shape, you get the triangular number above it. For
example, 15 – 5 = 10; 10 – 4 = 6; 6 – 3 = 3.
Following this pattern, if you take the bottom layer (2) off 3, you get 1. So 1 is a triangular number.
4. The tenth triangular number is 55 (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10).
Activity Three
a.

b. Answers will vary.
In each set of numbers, there is a pattern in the differences between the numbers.

Two adjacent triangular numbers added together equal the square number directly above the larger triangular number. For example, 3 + 6 = 9 and 15 + 21 = 36.

The differences between square numbers and the triangular numbers below them in the table form the set of triangular numbers (except for the initial zero).