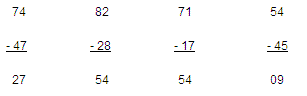Getting started
There are a number of mind reading programs around right now and if you go on the web you should find one or two to make you think.
Here is the outline of one mind reading game.
- “Want to let me read your mind?”
- “Write down a 3- or 4-digit number not all of whose digits are the same.”
- “Jumble the numbers to make another number and subtract the smallest number from the largest one.”
- “Circle one of the digits of your answer. Don’t circle a zero as that looks as if it is already circled.”
- “Type in the numbers except the one you’ve circled.”
- At this point the computer displays the number that you circled.
How did the computer do it?
Try a smaller case
Maybe we can do it with 2-digit numbers to start with. Since maths is about patterns, then we’ll look for patterns in what we do. So, what you should do now is to choose any 2-digit number, mix up its digits. (You can only actually reverse them.) Subtract the smaller number from the bigger one and see if there is any pattern.
I’ve done a few below to get you started.
With the several others that you can do you for yourself you should soon have quite a bit of ammunition. What do you notice about all of the answers?
Well, there are two things that you might see. In no special order these might be (i) all of the numbers are divisible by 9; and (ii) if you add the two digits of the answers, they all add up to 9. (You might note here that that is why we asked you not to choose numbers all of whose digits were the same because the pattern (ii) breaks down in such cases.)
The question now is, do these two patterns always hold?
To check out (i), think first of all what is going on in the first example. If we are subtracting 47 from 74, we can think of this as
70 + 4 – 40 – 7 = 70 – 7 + (4 – 40) = (70 – 7) – (40 – 4).
So at some point we’re taking 7 from 70 and 4 from 40. Both of these are multiples of 10 – 1. Now 10 – 1 = 9, so 40 – 4 = 4(10 – 1) = 4 x 9. And 70 – 7 = 7(10 – 1) = 7 x 9. So 74 – 47, which is the difference of 70 – 7, a multiple of 9, and 40 – 4, also a multiple of 9, has to itself be a multiple of 9.
But that’s true of any of our 2-digit subtractions. They all involve a couple of multiples of 10 – 1. So they must all be divisible by 9.
Now (ii) is perhaps easier though a little tedious. Write down all of the 2-digit multiples of 9 (including 09) and add the two digits together. There are not that many of them. Do you always get 9?
(You might speed this up if you know the rule for divisibility by 9. If you have forgotten it then refer to Guzzinta.)
But there’s a small question that occurs to me here. Does every 2-digit multiple of 9 occur as the difference of two numbers like the ones we’ve been thinking about?
3- and 4- digits
At this point I think that you might make some progress on this problem if you look at several examples of 3-digit numbers. Take a 3-digit number (with three different digits), mix up the numbers (you can do more than reverse the numbers this time), and subtract the smaller number from the larger number. What patterns do you see?
I’ll hang on here until you’ve done a few examples and have made some conjectures about what is happening.
Do you have the same conjectures that we did in section 3? In other words, did all of your examples result in (i) a number divisible by 9; and (ii) a number all of whose digits added to 9?
Consider (i). This seems to be looking good but let’s take a few examples. Suppose we try starting with 354. There are several ways to work with this number. Let’s look at a few.
543 534 354
- 354 - 354 - 345
189 180 009
All of these are certainly divisible by 9 but is that always the case?
To see this, let’s dissect the first example.
543 – 354 = (500 – 50) + (40 – 4) + (3 – 300) = (500 – 50) + (40 – 4) – (300 – 3).
But (500 – 50) = 5(100 – 10) = 5 x 90 = 5 x 9 x 10. This is a multiple of 9.
Now we know from section 3, that 40 – 4 is a multiple of 9.
And (300 – 3) = 3(100 – 1) = 3 x 99 = 3 x 9 x 11, another multiple of 9.
So 543 – 354 is a multiple of 9.
But this kind of dissection works in every case.
534 – 354 = (500 – 50) – (300 – 30) + (40 – 4) = 5(100 – 10) – 3(100 – 1) + 4(10 – 1);
354 – 345 = (300 – 300) + (50 – 5) – (40 – 4) = 3(100 – 100) + 5(10 – 1) – 4(10 – 1).
Both of these differences are divisible by 9.
In fact, no matter what numbers you start with, everything boils down to multiples of 100 – 100, 100 – 10, 100 – 1, 10 – 10 or 10 – 1. All of these are divisible by 9. So the 3-digit differences must always be divisible by 9.
And in the 4-digit case, we can reduce everything to looking at multiples of 1000 – 1000, 1000 – 100, 1000 – 10, 1000 – 1, 100 – 100, 100 – 10, 100 – 1, 10 – 10, or 10 – 1, all of which are divisible by 9.
But you can see that (ii) is false. The first example above gives 189 which gives 18 when you add all the digits together. But if you know the test for divisibility by 9 (Guzzinta) this shouldn’t surprise you. All you need is a sum of digits that is divisible by 9.
Getting it all together
So now it’s not too hard to see the trick. Whatever number you get after the subtraction, the sum of the digits is divisible by 9. So, if you show the computer 2 of the 3 digits it can work out the nearest sum that is a multiple of 9. Subtracting the 2 known digits from this sum gives the digit you’ve circled.
Let’s run through that slowly. Suppose that you chose 354 originally. Then suppose that after permuting the digits you got 534. A bit of work gives you 534 – 354 = 180. Now by the rules of the game, you can circle 1 or 8. Suppose you circled 8. Then you would show the computer 0 and 1. It calculates 0 + 1 = 1. The nearest multiple of 9 is 9 and you have to add 8 to 1 to get 9. And 8 is the very number that you circled.
At this point you can see why the computer forbad you to circle 0. If you had, in the example above where the answer was 180, you would show it 1 and 8. But 1 and 8 is 9. Now there are two candidates for the next multiple of 9. One of these is 0 and the other is 9. The computer can’t always get it right if it has a choice of two numbers. So it denies you the choice of 0.
Because the sums of all other answers with two digits are not multiples of 9, there is only one choice. The computer can handle this.
For four digits the same arguments apply.
As a result, the computer appears to be mind reading!
The seminar
How you approach this depends on your showmanship potential. You could do it with a great deal of show by asking your colleagues to write down a 3-digit number, permute the digits to make another 3-digit number, and take the smaller from the larger. Then get them to circle a non-zero digit from the three digits of their answer. (Remember 0 is a digit.) As they give you the other two digits, you, with a great deal of show, and mock brain activity, read their minds to tell them the two missing digits.
Or you could just get them to sit round a computer and let them to go through the programme.
After the show or the computer performance, try to lead them to see why the mind reading actually works.
And you might like to see if this thing works for 5-digit numbers!