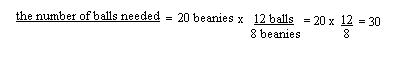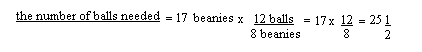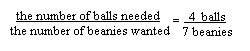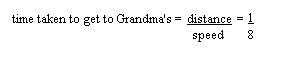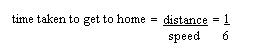Beanies, Bowlers, Painters, and Cyclists

Some problems

We want to talk about four problems and a funeral. The funeral is yours, mine and nearly everybody’s. It’s the mathematical area of ratios that, for some peculiar reason that we are not yet at the bottom of, seems to be so difficult. We’ll get to that later. But first the four problems.

Problem 1 – Beanies: It takes 4 balls of wool to make 7 beanies. How many balls of wool does it take to make 19 beanies?

Problem 2 – Bowlers: For the first half of the season, Martin had a better bowling average than Colin. For the second half of the season, Martin had a better bowling average than Colin. But Colin won the bowling trophy. How could that be?

Problem 3 – Cyclists: Hine takes rides his bike to his grandma’s house. He averages 8 kmh^-1 on the way there and 6 kmh^-1 on the way back. What is his average speed for the round trip?

Problem 4 – Painters: Freda by herself can paint the room in 5 hours. Fred by himself can paint the room in 7 hours. How long will it take them if they work together?

Four Problems Solved

Like any good problem solver, if at first you can’t see how to do these problems, you should experiment – change the numbers a bit and make them a lot ‘nicer’. Then see if that gives any insight into what is going on.

Problem 1 – Beanies

First of all we have to confess that we have no idea how much wool it takes to make a beanie. But that’s not the point. The point is to explore this situation and the ratios that are a part of it. So let’s start off to explore the situation with some slightly easier numbers than those in Problem 1.

What if 12 balls of wool make 8 beanies? How many beanies could you make with 24 balls of wool?

It’s clear that if you double the wool you double the beanies, so 24 balls make 16 beanies.

How many beanies will 36 balls of wool make? 36 = 3 × 12. So the number of beanies is 3 × 8 = 24.

What if we had 18 balls of wool? There are a number of ways of doing this. One way is to note that 18 = 12 + 6 and so we need to know how many beanies 6 balls of wool will make. Since 6 is half of 12, we’d expect to be able to make 4 (half of 8) beanies.

Since 12 makes 8 and 6 makes 4, then 18 makes 12.

Another way to do this problem is to realise that 18 is one-and-a-half times 12. So we need to calculate one-and-a-half times 8. To get one-and-a-half times something we have to multiply by 3/2. Now 8 x 3/2 = 12. So this way gives 12 beanies too.

So how many beanies can we get from 20 balls of wool? 20 = 12 + 8 = 12 + 6 + 2 = 12 + 4 + 4. Is it easier to work with 8, 6 + 2, or 4 + 4?

To get the answer for 8 we have to scale things. Going from 12 to 8 we have to multiply by 8/12 but this is the same as 2/3. So to see how many beanies we get we’ll have to multiply 8 (beanies) by 2/3. That’s a bit of a pain because it doesn’t give us a whole number but 8 x 2/3 = 16/3 = 5 1/3. So 20 balls of wool give us 8 + 5 1/3 = 13 1/3. We suppose that we really only get 13 beanies and have some wool left over for the next knitting job.

What about 6 + 2? Well we know that 6 balls gives 4 beanies, so we only have to work with 2. But 2 is a sixth of 12 so 2 balls of wool will produce a sixth of 8 beanies.
Now 8 x 1/6 = 8/6 = 4/3 = 1 1/3.
So 12 + 6 + 2 balls give us 8 + 4 + 1 1/3 = 13 1/3.

But if you are a 4 + 4 person then you could get there using 8 + 2 2/3 + 2 2/3 = 13 1/3 again.

Why take all this time? Why not note that to go from 12 to 20 you have to multiply by 20/12 = 5/3. So you have to multiply the 8 beanies by the same thing. And 8 x 5/3 = 40/3 = 13 1/3.

So there are many ways to do this kind of problem. However if you are confident with fractions you don’t have to mess about quite as much.

Of course there is still another way to do this kind of problem. 12 balls produce 8 beanies. So the number of beanies to balls of wool is in the ratio of 8 to 12. If you start with 24 balls of wool you can get the number of beanies by multiplying 20 by 8/12. So

24 balls of wool gives 24 x 8/12 = 24 x 2/3 = 16, and

36 balls of wool gives 36 x 8/12 = 36 x 2/3 = 24, and

18 balls of wool gives 18 x 8/12 = 18 x 2/3 = 12, and

20 balls of wool gives 20 x 8/12 = 20 x 2/3 = 40/3 = 13 1/3.

There appear to be at least three ways to do these kinds of problems. You can break up the number of balls into simple multiples of the 12; you can use the ratio of the new number of balls of wool to 12 and multiply 8 by that ratio; and you can take the ratio of 8 to 12 and multiply the new number of balls of wool by that fraction.

But we’ve approached this problem very much from the wools’ point of view. What if we took the beanies’ perspective? Remember that it takes 12 balls of wool to make 8 beanies. So how many balls will it take to make 16 beanies? Twice as many beanies; twice as many balls. 12 × 2 = 24. So 24 balls of wool.

How about 20 beanies? Well, 20 does equal 8 + 8 + 4, so we’ll need 12 + 12 + 6 = 30. But it should be clear that 1 beanie is made by 12/8 balls, so 20 is made by 20 × 12/8 = 20 × 3/2 = 10 × 3 = 30.

There are lots of ‘simple’ numbers of beanies where finding the number of balls of wool is a just a matter of breaking the 8 into the right quantities and it’s easy to find the number of balls. The ratio approach shows a much deeper understanding of what is happening and enables the number of balls of wool for any number of beanies to be assessed. Let’s look at the 20 beanies problem again. The fact is that

So if we want to make 20 beanies we are faced with

beaniesEqn2.

And so we get

beaniesEqn3.

If we wanted to make 17 beanies it’s easiest to go straight to the multiplication

beaniesEqn4.

But the original problem said that it took 4 balls of wool to make 7 beanies, so how many balls would we need to make 19 beanies? Well

beaniesEqn5.

So that probably means that we need to go out and buy 11 balls of wool.

Problem 2 – Bowlers

This seems a totally ridiculous problem. How could a bowler who topped the averages in both halves of the season end up not getting the bowling trophy? After a few simple examples it starts to look even more ridiculous. But first, what is the ratio here and how does it work?

To get a bowler’s average you simply find out how many runs he’s conceded and divide that by the number of wickets he’s taken. So if Martin has conceded 20 runs and taken 4 wickets, his average is 20/4 = 5.

Now if you are easing the class into this problem you might like to warm them up by getting them to work out a few averages. With simple numbers that might be reasonably straightforward. But you could get into big numbers by asking what a bowler’s average would be over a season if he had had 6000 runs hit off of him and had taken 100 wickets.

There are clearly two more variations of this problem and two more variations within each variation. It all depends on what unknown of average, number of wickets, and number of runs taken, that you want to find. And it also depends on the order you place the givens in the sentence.

Make the unknown the runs conceded: For example,

(i) if a bowler’s average is 7 and he has taken 20 wickets, how many runs have been hit off of his bowling? and

(ii) if a bowler has taken 20 wickets and his average is 7, how many runs have been hit off of his bowling?

Make the unknown the number of wickets taken: For example,

(i) if a bowler’s average is 8 and he has conceded 96 runs, how many wickets has he taken? and

(ii) if a bowler has conceded 96 runs and his average is 8, how many wickets has he taken?

We call these problems inverse problems because you have to do things in what seems to be an unnatural order. As always with these ratio problems, the inverse problems are harder than the straightforward ‘given runs and wickets, find the average’ problems.

We worked inversely with the wool and beanies problem. Working with the number of beanies known and the number of balls of wool unknown, is the inverse of the cases where the number of balls of wool is known and the number of beanies is unknown. It also seems to be harder too because the original problem is posed the other way round.

It may well be that these inverse problems are unnatural because most of the time in real life they are not the kind of problem that actually comes up. Have you heard radio or TV commentators asking “If Fred has conceded 96 runs and his average is 8, how many wickets has he taken?” But it’s the inverse problems that test whether the student really understands what is going on. If they can get their heads around these problems then they know the problem ‘inside out’.

OK so now we are on top of this averages business. It’s time to get down to the problem of the two halves of the season. So let’s experiment first and hope that an idea pops into our heads.

Suppose that Martin got 4 wickets up to Christmas while conceding 20 runs. His average would be 5 at that point. Then after Christmas suppose that he took 1 wicket for 15 runs at an average of 15. Then altogether, he would have had 35 runs knocked off his bowling and would have taken 5 wickets. 35/5 = 7. His season average was 7.

Chris on the other hand might have taken 6 for 30 in the first half of the season for an average of 5 (more than Martin’s 4) and 2 for 32 in the second half of the season for an average of 16 (more than Martin’s 15). This gave him 8 for 62 for the season at an average of 7.75.

But Martin wins the bowling trophy! Surely this is just what we would expect?

Let’s tweak Chris’ figures. If he took 12 for 60 before Christmas he’d still have an average of 5 for that period. His season statistics though, would be 14 for 92 for an average of 6.57. Hang on that’s less than Martin’s 7!! What’s going on here?

To make the point even more say he had taken 24 for 120 rather than 12 for 60. This is still a half season average of 5 but his season’s bowling of 26 for 152 averages out at 5.85. That’s considerably less than Martin’s 7.

Suppose Chris took 1000 for 5000. Then his season figures would be 1002 for 5032 for an average of 5.02. Can you see that Chris’ average is getting closer and closer to 5 as the number of runs and wickets increases? You see these numbers are starting to swamp out the relatively miniscule 2 for 32.

So now it is just a matter of a judicious choice of statistics and you can get Chris the trophy.

Before we finish it’s important to underline the fact that you don’t add averages the same way that you add fractions. You have to accumulate all the runs and all the wickets and do the dividing again. It’s a bit like adding students test marks. If Jo got 8/10 for one test and 9/10 for another, she would have got 17 marks out of 20 and we might want to express this as 17/20. However,

but 17/20 and 17/10 are two completely different numbers. So you need to be careful when adding fractions as one of the uses that students may have had for fractions is as test scores.

If you did ‘add’ averages the way that you add fractions then the problem would work out differently. Obviously if you add two bigger fractions together you get a number that is bigger than when you add two smaller fractions together. Or is that really obvious? Indeed is it even true? We’ll leave you to figure that out for yourselves. You might find a number line useful.

roblem 3 – Cyclists

The cyclist problem is one that bears exploration too because it doesn’t work out as neatly as you might expect. If Hine goes one way at 8kmh^-1 and the other at 6kmh^-1 any sensible person might think that he will average 7kmh^-1 overall. But it’s more complicated than that. To be sure, let’s calculate the distance he rode and the time that he took to go that far. Then we can work out the average speed.

Let’s take it step by step. First, the trip to grandma’s house.

house.

Now one vital piece of information has been left out of the problem. We were never told how far it is from Hine’s to grandma’s. So we’ll make things easy for ourselves and assume that it is just one kilometre. If Hine rode at 8kmh^-1 how long did it take him to get there?

Now speed = distance/time and so time = distance/speed.

So for Hine, the

cyclisteqn1.

and the units are hours, so it took Hine an eighth of an hour to get to grandma’s.

Second, we look at the trip back home from grandma’s. So for Hine, the

cyclisteqn2.

a time of one sixth of an hour.

OK, so he took 1/8 + 1/6 = (3 +4)/24 = 7/24th of an hour. In that time he travelled 2 kilometres. So his average speed was 2/(7/24) = 48/7 = 6 6/7kmh^-1. Not far from 7 kmh-1 but not quite equal to it!

Would it make any difference if we had assumed that Hine lived 2 km from his grandma? Or 3 km? Or 10km? We’ll leave that for you to work out.

This is an example of a problem where there are ratios (distance over time, etc.) but where they have to be treated with kid gloves. You can’t just rush in and blindly apply rules that you have learnt, especially when they don’t apply in the case you’re working with.

Problem 4 – Painters

It’s almost a sure thing that even though Freda takes 5 hours to paint the room by herself and Fred takes 7 hours, that together they won’t do it in 6 hours. So if not, why not? Well the first thing to notice is that if Freda only takes 5 hours by herself, then together they should take less than 5 hours. But how less?

Let’s take an easier problem first. Suppose that Freda took 2 hours to paint the room and Fred took only 1 hour. How long would they take to paint it together?

One way to do this is by using a table. Since Fred takes 60 minutes to paint the room, together they must take less time, so we’ll start out with 50 minutes as a guess.

Time (minutes)	Amount painted		Total amount painted	More/less than one room
	By Freda	By Fred
50	50/120	50/60	15/12	more
30	30/120	30/60	8/12	less
45	45/120	45/60	135/120	more
40	40/120	40/60	12/12 = 1	equal

By thinking about what was going on, it seems that what we really wanted to know was what we had to multiply 1/120 + 1/60 = 3/120 by to get 1. Well, 3/120 = 1/40, so we need to multiply this by 40 to get 1. So it took 40 minutes.

But what is the significance of 1/120 and 1/60 and why should we add those two things together? If it takes Freda 120 minutes to paint the whole room then she can paint 1/120 ths of it in 1 minute. In the same time, Fred can paint 2/120 ths of the room. So in 1 minute they can paint 3/120 ths of the room. How many minutes does it then take for them to paint the whole room? How many times 3/120 is 1? Just 40.

If you don’t freak out at a little algebra, there is another way to look at this. Now Fred works twice as fast as Freda. So he will paint twice as much of the room as she does. So if the amount of the room that she paints is x, then he paints 2x. And together they paint 1 room, so 3x = 1 or x = 1/3. Freda paints 1 room in 2 hours so she will take 2/3 of an hour to paint 1/3 of a room. (And Fred can paint 2/3 of the room in 60 × 2/3 = 40 minutes too.) So they can paint the room in 40 minutes.

Now we can confidently tackle the original problem. Remember Freda takes 5 hours and Fred 7. You can do the table method. We’ll notice that Freda can paint 1/300 ths of the room in 1 minute and Fred can paint 1/420 ths of the room in the same time. So, in 1 minute they can paint 1/300 + 1/420 = (7+5)/2100 = 12/2100.hat do we have to multiply this by to get 1? Surely just 2100/12? So that’s how long they take to paint the room. And 2100/12 = 175 minutes or 2 hours and 55 minutes.

Doesn’t that seem a big drop from 5 or 7 hours?! Would we really expect the job to be done in this short a time? Let’s check it algebraically to see if we get the same answer.

Suppose that Fred paints x of the room. Then Freda will paint 7x/5 as she paints 7/5 times faster than he does. So together they paint x + 7x/5= 12x/5is is equal to 1, so x = 5/12. Now Fred paints the whole room in 7 hours so he paints 5/12 of it in 5/12 × 7 = 35/12 hours or 35/12 × 60 = 175 minutes. It’s the same answer again. It must be right!

Did you get the that answer by using a table? Well let’s think about it a bit to see why the time is not so surprising. What if Freda and Fred both took 5 hours? Surely they’d do the whole room in 5 hours. No! If they work at the same pace, then they’ll each do half of the room. So they’ll finish in 2 hours 30 minutes. Ah, that makes the answer to the 5 and 7 hour problem seem a lot better.

What about the inverse problem though? What if Freda can paint the room in 5 hours and together they can paint the room in 3 hours. How fast can Fred do it on his own? Can you undo what we have done to find the answer? Or is it easier to use a table? And if it is, does this give you the clue for answering the inverse problem?

And what if Freda can paint a room in 5 hours, Fred can paint it in 6 hours and Hinu can do it in 7 hours? How long can they do it working together? There’s no end to the fun you can have with paint.

Possible seminars

Each one of these problems could be a seminar in itself. You know your staff better than we do so you should make the most appropriate choice from the possibilities below.

Seminar 1

A. Pose Problem 1.

Let the staff attempt the problem as it is originally stated.

Discuss the answer and the methods that they used to achieve the answer. (Make sure that more than one method is discussed. It doesn’t matter how ‘simple’ those methods may appear to be.)

B. Which of the students in your classes would be able to solve that problem with no help?

How would they solve it?

Whereabouts would those students be on the Number Framework?

Which of the students in your classes would be able to solve that problem with some help?

How would they solve it?

What help would you need to give them?

Whereabouts would those students be on the Number Framework?

Which of the students in your classes would not be able to solve that problem using any method you can think of?

Whereabouts would those students be on the Number Framework?

C. Now change the numbers to make the problem easy as in our first variation.

Repeat the questions of B.

What is there about this problem that makes it easier to solve?

D. Repeat B with successively more difficult versions of the problem.

What is there about this problem that makes it easier to solve?

E. What have you all learned from this seminar?

Seminar 2

A. Pose Problem 2.

Let the staff attempt the problem as it is originally stated.

Discuss the answer and the methods that they used to achieve the answer. (Make sure that more than one method is discussed. It doesn’t matter how ‘simple’ those methods may appear to be.)

B. Which of the students in your classes would be able to solve that problem with no help?

How would they solve it?

Whereabouts would those students be on the Number Framework?

Which of the students in your classes would be able to solve that problem with some help?

How would they solve it?

What help would you need to give them?

Whereabouts would those students be on the Number Framework?

Which of the students in your classes would not be able to solve that problem using any method you can think of?

Whereabouts would those students be on the Number Framework?

C. Now that you have seen how to do the problem can you find another set of averages that would solve the problem?

If you did the problem once in front of all the class, how many students, without help, would be able to see how to get another set of averages that would settle Problem 1?

Repeat the questions of B.

D. Introduce some of the straightforward average problems (not the inverse ones yet).

Repeat the questions of B.

Why are these questions easier than Problem 2?

E. Now pose some of the inverse problems.

Repeat the questions of B.

Why are these questions easier than Problem 2 but harder than those in D?

F. What have you all learned from this seminar?

Seminar 3

A. Pose Problem 3.

Let the staff attempt the problem as it is originally stated.

Discuss the answer and the methods that they used to achieve the answer. (Make sure that more than one method is discussed. It doesn’t matter how ‘simple’ those methods may appear to be.)

B. Which of the students in your classes would be able to solve that problem with no help?

How would they solve it?

Whereabouts would those students be on the Number Framework?

Which of the students in your classes would be able to solve that problem with some help?

How would they solve it?

What help would you need to give them?

Whereabouts would those students be on the Number Framework?

Which of the students in your classes would not be able to solve that problem using any method you can think of?

Whereabouts would those students be on the Number Framework?

C. Now that you have seen how to do the problem can you do it again but this time by assuming that the distance between Hine’s and grandma’s houses is 3 km.?

If you did the problem once in front of all the class, how many students would be able to see how to do it by themselves this time?

Repeat the questions of B.

D. Now try an inverse version of the problem. Give them Hine’s average speed, his average speed from his house to grandma’s, and ask them what was his average speed on the way home.

Repeat the questions of B.

Why is this question harder than Problem 3?

E. Let the teachers each make up their own version of Problem 3.

Repeat the questions of B.

F. What have you all learned from this seminar?

Seminar 4

A. Pose Problem 4.

Let the staff attempt the problem as it is originally stated.

Discuss the answer and the methods that they used to achieve the answer. (Make sure that more than one method is discussed. It doesn’t matter how ‘simple’ those methods may appear to be.)

B. Which of the students in your classes would be able to solve that problem with no help?

How would they solve it?

Whereabouts would those students be on the Number Framework?

Which of the students in your classes would be able to solve that problem with some help?

How would they solve it?

What help would you need to give them?

Whereabouts would those students be on the Number Framework?

Which of the students in your classes would not be able to solve that problem using any method you can think of?

Whereabouts would those students be on the Number Framework?

C. Now change the numbers to make the problem easy as in our first variation.

Repeat the questions of B.

What is there about this problem that makes it easier to solve?

D. Repeat B with successively more difficult versions of the problem (including the case when Fred and Freda both paint the room in the same time).

What affects the difficulty of these problems?

E. What have you all learned from this seminar?

Seminar 5

A. Pose each of the problems 1, 2, 3, and 4. Let the staff attempt the problems as they were originally stated.

Discuss the answers and the methods that they used to achieve the answer. (Make sure that more than one method is discussed. It doesn’t matter how ‘simple’ those methods may appear to be.)

B. Which of the students in your classes would be able to solve the problems with no help?

How would they solve them?

Whereabouts would those students be on the Number Framework?

Which of the students in your classes would be able to solve the problems with some help?

How would they solve it?

What help would you need to give them?

Whereabouts would those students be on the Number Framework?

Which of the students in your classes would not be able to solve any of the problems using any method you can think of?

Whereabouts would those students be on the Number Framework?

C. Get them each to rate the problems in order of difficulty.

Which is the most difficult problem?

Is the same problem the most difficult for everyone?

Go down the list asking the same two questions.

D. What have you all learned from this seminar?