Introduction
The format on this one is as follows. First we pose and answer the straightforward problems relating to one throw of a dice (section 2). Then we see that there might be a more relevant question if you are actually playing snakes and ladders (section 3). This leads us into a contradiction with two different answers being given for the probability of the same event. In section 4 we look to spinners to try to understand what is going on. Then, in section 5 we are able to use spinners to resolve the matter as far as the snake is concerned. This leads us to looking at the ladder situation in section 6. In section 7 we reflect on what we’ve done. Finally we suggest an approach that you might take in the staff room discussion (section 8). At the end (section 9), there are some OHTs for you to copy if you think that they might help.
There is no need to go as far as we have done here. Leave something up your sleeve if you want to or add a problem from a different dice game or give them some homework. The final seminar is up to you. We have just provided some suggestions.
You might find it useful to have a Snakes and Ladders Board handy. If you do, you’ll probably find that there won’t be a snake or a ladder just where I have placed them in the diagram. In that case you may need to change the problem slightly to make things fit your Board.
There are two other staff room meeting suggestions for probability. These come under Monopoly and Lotto. On reflection Snakes and Ladders is most likely the easiest, Monopoly is a little more difficult and Lotto is the hardest. If you are going to do all three you may want to do them in that order. However, this will depend on your staff.
Problem 1 – Snakes and Ladders
Playing Snakes and Ladders, we’ve landed on square 41. What are our chances of landing on the snake on square 43? How about the chances of landing on the ladder? Or of missing both of them?
.gif)
This by itself is not too difficult but needs a small lead in. First of all, how do we find probabilities. Well, we need to know what things can happen and what things we would like to happen. The chances of something happening are given by the following:
![]() .
.
‘Event’ is just a stuffy mathematical way of saying ‘something that you are interested in’. ‘All possible outcomes’ is ‘everything that could happen at that point’.
What does this mean for us in the Snakes and Ladders example? What we are interested in there is ‘landing on the snake’. This can be done only if we roll a 2. This can only happen in one way. What are all possible outcomes? Well we can only throw 1, 2, 3, 4, 5, or 6. There are six things that could happen. So
![]()
You then have one chance in six of landing on the snake on this next throw. In the same way you can see that there is the same probability of landing on the ladder. The only difference in the working is that to land on the ladder you need to throw a 4. But there’s only one way that this can happen so again you get one (the number of ways the event can happen) divided by six (the number of possible outcomes when you roll a single dice).
But how about missing them both? There are two ways of going about this – the direct way and the indirect way. First we’ll go the direct way. Using the method we used above, there are four ways of missing both the snake and the ladder. This is done by rolling 1, 3, 5 or 6. This can happen in four ways. Once again there are six outcomes when you roll a dice. So the probability of missing both the snake and the ladder is 4/6. (This actually simplifies to 2/3 but you don’t need to worry about this.)
So now we have to go the indirect way. To do this we need to remember that the chance of everything happening is one. This is because
![]()
![]() .
.
So
Probability that we miss the snake and ladder + Probability that we hit the snake and ladder = 1.
So
Probability that we miss the snake and ladder + Probability that we hit the snake + Probability that we hit the ladder = 1.
We can break up the snake and the ladder probabilities because they don’t rely on each other. The chance of landing on the snake doesn’t depend on the chance of landing on the ladder. The events are independent.
So
Probability that we miss the snake and ladder + 1/6 + 1/6 = 1
So
Probability that we miss the snake and ladder = 1 – 1/6 – 1/6 = 1 – 2/6 = 4/6 (or 2/3).
More Snakes and Ladders
In the Snakes and Ladders problem that we tackled above, we were only worried about landing on the snake or the ladder (or missing them both) in our next throw. But even after we’ve thrown and missed (or not hit) the snake or the ladder, we may still get them in a subsequent throw. The thing that most likely really interests us is ‘are we going to miss the snake this time round?’ or ‘are we going to get onto the ladder this time round?’ So let’s see what the chances are of being snagged by the snake. Or maybe even better, when we are really playing the game, what are the chances of passing the snake given that we are right now on square 41.
We need to do a bit of analysis first. How could we land on the snake? Well we could get a 2 and do it straight away. If we got a 3, 4, 5 or 6 we would be out of the snake’s clutches. But if we got a 1, we might get another 1 on the next throw and get ‘snaked’.
If we show that in a table we get
| event | snake | miss |
| 1 + 1 | a | |
| 1 + 2 | a | |
| 1 + 3 | ||
| 1 + 4 | a | |
| 1 + 5 | a | |
| 1 + 6 | a | |
| 2 | a | |
| 3 | a | |
| 4 | a | |
| 5 | a | |
| 6 | a |
Now the probability of getting a 1 followed by a 1 is 1/36. This is because there is only one way to get a 1 and there are 36 possible outcomes of rolling a dice (six possibilities from one dice multiplied by the six possibilities from the other dice).
On the other hand, there is a 1/6 chance of getting a 2. So altogether there must be a 1/36 plus a 1/6 chance of getting snaked. 1/36 + 1/6 = 7/36. The probability of landing on the snake is 7/36.
That seems fine until you remember that
![]()
Because from the table we see that there are just two ways that we can land on the snake. And there are 11 possible outcomes.
So this means that
![]()
Is 7/36 = 2/11? If not we are in trouble. They’re not; so we are.
Spinners
When in doubt try something simpler. What can be simpler than spinners. If you would like a template for making them go to I'm Spinning.
This will also give you some practice in simple probability if you think that you need it.
Let’s think about the first spinner below, spinner 1. There are four possible outcomes, A, B, C, and D. So the probability of each one is ¼ using the basic formula.
.gif)
spinner 1
That all seems reasonable. So let’s look at spinner 2. There are three possible outcomes so the probability of getting each one is 1/3. This is because the number of ways of getting each individual letter is 1 and there are 3 possible outcomes.
.gif)
spinner 2
Doesn’t that seem fishy to you? Shouldn’t the probability of getting a C be bigger than that of getting an A or a B? In fact wouldn’t you expect to get C twice as often as A or twice as often as B? Make up the spinner and try spinning it thirty (or more) times. How often did you get A or B or C? Did you get them about 10 times each?
It rather looks as if the probability of getting A should be ¼, the same as it was with spinner 1. The same goes for the probability of getting B. But for C we surely should get the sum of the probabilities of C and D that we got with spinner 1. And ¼ + ¼ = ½!
So where does the problem lie? Well it lies with the use of the basic formula for probability. That formula only works if each of the events that we are interested in have equal probability. So we can analyse spinner 1 quite well with it but we can’t analyse spinner 2 with the formula because the probabilities of getting A, B, and C are not all the same.
Or we can look at it another way. We can think here of the probability as being an arc problem.
.gif) .
.
When you think about it that is essentially what the original probability definition was. So using this formulation we get the answers that make sense to us.
probability of getting A = ¼;
probability of getting B = ¼;
probability of getting C = 2/4 = ½.
Spinners for snakes
Was this the problem with the probability of landing on a snake in section 3? Were all of the probabilities not the same? That was surely the case. The probability of getting a 1 followed by a 1 is much smaller than the probability of getting a 3. So we can’t apply the formula.
So what we’ll do to settle the issue is to make a spinner that represents the snake problem. Start of with six equal sectors to represent getting a 1, 2, 3, 4, 5, or 6. These all have equal arcs so they will have equal probabilities of 1/6. So far so good.
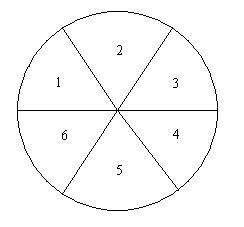
spinner 3
This would be fine if we only wanted to model the throws of a dice but we are after something else. So we need to add a space for the 1 + 1 throws. That means that we have to divide the sector with the 1 into six equal parts that represent 1 + 1, 1 + 2, 1 + 3, 1 + 4, 1 + 5, 1 + 6. We have done this in spinner 4 below. Because of size problems we have only marked the 1 + 1 on the spinner.
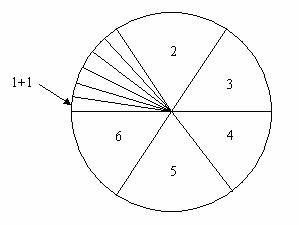
spinner 4
Now we can use the arc form of the basic formula to give any probability that we like. What we like here is the probability of getting on the snake. This is given by
.
Perhaps not surprisingly we get 7/36. This then validates the approach we took earlier that gave us precisely 7/36. We could just add together the probability of getting 1 + 1 and the probability of getting 2
… and ladders
Now we could carry out exactly the same analysis for the chances of landing at the foot of the ladder on square 45. First what will give us ‘success’? We can see that in the table below. It’s a little more complicated than the snake situation.
| event | ladder | miss |
| 1 + 1 | a | |
| 1 + 2 + 1 | a | |
| 1 + 2 + 2 | a | |
| 1 + 2 + 3 | a | |
| 1 + 2 + 4 | a | |
| 1 + 2 + 5 | a | |
| 1 + 2 + 6 | a | |
| 1 + 3 | a | |
| 1 + 4 | a | |
| 1 + 5 | a | |
| 1 + 6 | a | |
| 2 | a | |
| 3 + 1 | a | |
| 3 + 2 | a | |
| 3 + 3 | a | |
| 3 + 4 | a | |
| 3 + 5 | a | |
| 3 + 6 | a | |
| 4 | a | |
| 5 | a | |
| 6 | a |
At this point, we can make up our spinner and calculate the probability or use the easier route below. All we have to do is to add together the probabilities of the various successful events. These are:
probability of 1+2+1 = 1/216 (only one success in three rolls of a dice);
probability of 1+3 = 1/36;
probability of 3+1 = 1/36;
probability of 4 = 1/6.
So the probability of landing on the ladder is 1/216 + 1/36 + 1/36 + 1/6 = 49/216.
Reflections
It’s worth noting a couple of things at this point. First, we have to be careful about how we use formulae. The basic one for probability is OK if it is used correctly. No formula can be applied blindly because it’s only good for certain conditions.
Second, let’s look at the answers that we got.
probability of getting the snake in one throw = 1/6;
probability of getting the snake = 7/36;
probability of getting the ladder in one throw = 1/6;
probability of getting the ladder = 49/216.
Are they reasonable? Well you might check that practically. Perform the experiments. Get out a dice and roll for a hundred rolls or so and see how things pan out. Do the simulation. Write a computer program and run it for 10000 times. What do you get?
It’s comforting that the probabilities of getting either object are both bigger than just getting it in one throw. 7/36 > 1/6 and 49/216 > 1/6. In the first case there is relatively little difference. In the second case there’s quite a bit – about 0.23 compared with 0.17.
Staff Seminar
You will probably be able to cover most of the material above in one session. To do this you will need to remind the staff of the basic definition of probability. It may help to then cover some simple examples. Ask them to work out
- the probability of throwing a Head when you toss a coin (1/2);
- the probability of getting a 5 when you roll a dice (1/6);
- the probability of getting a C when you spin spinner 2; and
- the probability of getting a blue ball when you draw a ball from a box that contains 3 red and 2 blue balls (2/5).
Then pose the first type of Snakes and Ladders problem (what is the chances of landing on the snake, etc., in one throw of the dice) and let the staff tackle it to see what they get. Discuss the answers.
Then go to the second type that doesn’t limit the number of throws. If the staff comes up with two or more answers, fine. This provides meat for discussion. If they don’t you may need to prompt them into thinking that there may be at least two ways to do the problem. And that they give two different answers! Let them discuss that surprising situation.
Summarise what has been achieved at the end.
Overhead Transparencies
The snakes and ladders board.
.gif)
The two tables
| event | snake | miss |
| 1 + 1 | a | |
| 1 + 2 | a | |
| 1 + 3 | ||
| 1 + 4 | a | |
| 1 + 5 | a | |
| 1 + 6 | a | |
| 2 | a | |
| 3 | a | |
| 4 | a | |
| 5 | a | |
| 6 | a |
the snake table
| event | ladder | miss |
| 1 + 1 | a | |
| 1 + 2 + 1 | a | |
| 1 + 2 + 2 | a | |
| 1 + 2 + 3 | a | |
| 1 + 2 + 4 | a | |
| 1 + 2 + 5 | a | |
| 1 + 2 + 6 | a | |
| 1 + 3 | a | |
| 1 + 4 | a | |
| 1 + 5 | a | |
| 1 + 6 | a | |
| 2 | a | |
| 3 + 1 | a | |
| 3 + 2 | a | |
| 3 + 3 | a | |
| 3 + 4 | a | |
| 3 + 5 | a | |
| 3 + 6 | a | |
| 4 | a | |
| 5 | a | |
| 6 | a |
the ladder table
The four spinners
.gif)
spinner 1
.gif)
spinner 2
.jpg)
spinner 3
.jpg)
spinner 4