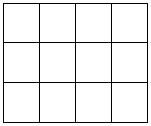
The key idea of measurement at level 4 is the application of multiplicative thinking to measurement.
Multiplicative thinking involves the mental co-ordination of two factors and is often introduced to students using an array where one factor is the number of rows, and the other factor is the number of columns. This model is directly related to the calculation of area for rectangular shapes where each of the factors represents one of the lengths of parallel sides. For example, the diagram below can be used to represent both the multiplication 4 x 3 = 12, and the area of a large table which is 4 metres wide and 3 metres long, 12m2.
The array model clearly supports an understanding of the base x height formula used to calculate area. This understanding can be used as the basis for introducing other measurement formulas. For example, parallelograms can be viewed as rectangles that have been tilted to make the sides slanted, so the “base x height” formula works with these too. Triangles can be viewed as half a parallelogram and so the formula “½ base x height” can be applied.
Area and volume formulas provide a method of measuring these attributes using only measures of length and need to be introduced with supporting conceptual background. As students develop their knowledge of the relationships involved in composite measures they can be introduced to formula which describe these measures.
Conversion between metric units involves multiplication or division by a power of 10. For example, converting 1.2km to metres involves multiplication by 1000 (1200m), converting 14.3 centimetres to metres involves division by 100 (0.143m). It is important for students to develop an appreciation of the need to use units that are appropriate for the situation. For example the diameter of a button is most appropriately measured in millimetres, while the distance between Dunedin and Christchurch is best described using kilometres.
At this level students also explore measurements which involve the comparison of two quantities expressed as a rate. For example a comparison of the distance travelled and the time taken becomes a measure of speed such as km/h.
This key idea develops from the key idea of measurement at level 3 which involves the use of standard scales.
This key idea is extended to the key idea of measurement at level 5 where students focus on the approximate nature of all measurements.