Effective teachers support students in creating connections between different ways of solving problems, between mathematical representations and topics, and between mathematics and everyday experiences.
Guidance for effective practice:
- Use a single context in the first few lessons about a mathematical idea, and explore variations to the context, and consider the effect of that variation.
Esa begins her unit on division with a single problem, “Some sisters are given 36 marbles to share equally. How many marbles does each sister get?” Students explore possible answers by varying the number of sisters, using materials if needed.
Esa’s students generalize that the more sisters there are, the smaller is the number of marbles they each get. They record their answers with equations, e.g., 36 ÷ 3 = 12 organized in a pattern. The next few lessons are spent exploring variations to the same problem. For example, “If there are four sisters, how many marbles would give them an equal share with no left-overs?” and “Some sisters share some marbles. Each sister gets 8 marbles. How many marbles and sisters are there?”
Esa starts with a single division problem, 36 ÷ [ ] = [ ], and explores the effect on changing the location of the unknown.
- Pose problems in contexts that help ākonga connect mathematics to their daily lives.
Bik knows that her students are excited about the Rugby World Cup to be held in France. The boys and girls are obsessed with rugby and play the game every lunchtime. She also wants to know if her students can solve problems that combine the four operations.
She starts the lesson with a fake headline:
Wallabies 30 All Blacks 27
Boring, booting Aussies beat enterprising, careless All Blacks.
Is that possible?
How did each team score their points?
Bik uses a context that is of high interest to her students and that affords investigation of important mathematical ideas.
- Help ākonga to attend to pattern and structure.
Pattern is about consistency, something that always occurs. Structure is about organization, the way the elements in a pattern relate, and why that occurs.
Shirvani has a Year 1 class. She notices that generally her students find repeating patterns challenging. Many of her students lack routines in their life and are beginning to find comfort in the predictable sequence of events in a school day.
Shirvani decides to integrate pattern and shape in a unit of work. As well as using everyday objects like leaves and stones to make patterns, she uses sets of attribute (logic) blocks that she finds in the resource room. Her students find the blocks appealing.
In one lesson she starts by building these patterns on the mat, introduced one after the other:
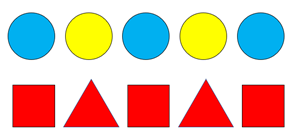
Shirvani: What do you notice? Talk to another person first.
Her students name the colours and shapes, and she highlights important words like triangle and circle.
Shirvani: If I wanted to carry this picture on all the way out the door, pointing in the right direction, what shapes would I need?
Some students are unsure about what comes next. Shirvani supports them to read the patterns, “Blue circle, yellow circle, blue circle, …” Together they extend the pattern further using attribute blocks.
Shirvani: Think hard. What is different about the two patterns, and what is the same?
Shirvani is hoping that her students will notice the A, B, A, B, A, B, … structure of both patterns, and possibly identify the part (unit) that repeats in each case.