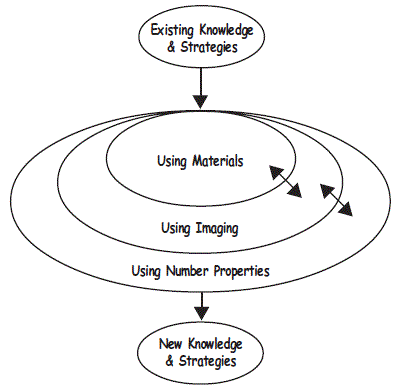
The teaching model has been adapted from Pirie and Kieren’s Recursive Theory of Mathematical Understanding (1994). Two of the key ideas of their theory are that children's mathematical understandings are not learned in a linear fashion and that children may need to move between different phases by folding back. In the numeracy teaching model that idea of ‘folding back’ is illustrated by the arrows.
Materials
Teachers in New Zealand, particularly of junior classes, are familiar with using materials when introducing new concepts in mathematics. However, a common belief was that children could move from using materials to abstraction. As many children cannot easily make that step to abstraction they need to be assisted to build images (in their minds) that they can access.
In the using materials phase a teacher may use number lines shaded in groups of 5 and transparent counters to help build visual images in the children’s mind. It is not enough that they see 6 + 3 = 9 but that they become aware that where the shaded areas change colour another group of 5 has been made. So 5 + 4 = 9 and they can show it as a pattern on their fingers.
Imaging
The using imaging phase is the bridge to help make the connection between concrete and abstract cognition. As students become more proficient in solving problems using counters and number lines, the teacher may turn the lines over thus shielding the sequence from the children and encouraging them to image the materials operation. Within any lesson, particularly with older children, teachers need to try and ‘force’ the imaging by moving backwards and forwards between the material and imaging phases. If children are having trouble imaging, the teacher provides the materials again. Children need to be secure in using imaging before they enter the using number properties phase.
Number Properties
When numbers are larger than students can easily track in their minds it is expected they will connect to number properties without the use of imaging. As well as large numbers the number properties phase also looks at what students notice about the numbers they are working with. For example when asked how he would work out 65 + 6 a 6 year old student replied, very quickly, 71. When asked for his strategy he said, “I know 6 and 5 equals 11 so it must be 71." Not the expected response of add 5 then 1. As students have difficulty the teacher can decide, as before, to re-introduce the imaging phase or even the materials phase again. To move children from the use of naīve strategies to more sophisticated ones can be difficult.