New Zealand Curriculum: Level 3-4
Learning Progression Frameworks: Multiplicative thinking, Signpost 6 to Signpost 7
Target students
These activities are intended for students who have some previous experience with treating fractions as number, including a good understanding of the meaning of numerator and denominator. It is preferable that students have knowledge of multiplication facts.
The following diagnostic questions indicate students’ understanding of, and ability to represent the part-whole relationships in one or more ratios as fractions. A connected cube model is used to find out students’ ability to recognise the fractions created within ratios. The questions are in order of complexity. If the student answers a question confidently and with understanding proceed to the next question. If not, then use the supporting activities to build and strengthen their fluency and understanding. Allow access to pencil and paper. (show diagnostic questions)
The questions should be presented orally and in a written form so that the student can refer to them.
- Here is a mixture of blueberry and apple juice. The blue represent units of blueberry juice and the green represent units of apple juice. (Ratio 1:3)
What fraction of the mixture is blueberry?
What fraction is apple?
Signs of fluency and understanding:
Identifies that there are four units in total, so each cylinder is equivalent to one quarter of the mixture. Gives the fraction of blueberry as one quarter and the fraction of apple as three quarters.
What to notice if your student does not solve the problem fluently:
Expresses the part-to-part relationship as the fraction, one third (as in one to three). This indicates that the student has difficulty identifying the whole and expressing each part as a fraction of that whole.
Notices that the number of blueberry units is one and the number of apple units is three but cannot express the part to whole relationships as fractions. This may indicate that the student has difficulty naming a fraction of a set.
Supporting activities:
Identifying fractions in simple ratios
- What fraction of this mixture is blueberry?
What fraction is apple?
Can you give equivalent fractions for blueberry and apply?
Signs of fluency and understanding:
Identifies that the mixture has ten units. Recognises that four units are blueberry, and six units are apple, gives the fractions four tenths blueberry and six tenths apple. Works out that putting the units into pairs create fifths. So the equivalent fractions are two fifths blueberry and three fifths apple.
What to notice if your student does not solve the problem fluently:
Names the fractions as four tenths and six tenths but cannot name the equivalent fractions. This indicates the students needs to work on equivalent fractions in sets contexts.
Names the part-part relationships as fractions, namely four sixths (as in four to six). This indicates that the student needs support with identifying and naming part-whole relationships.
Identifies the numbers of blueberry and apply units but cannot name the part-whole fractions. This indicates that the student needs opportunities to identify fractions in sets contexts.
Supporting activity:
Equivalent fractions in simple ratios
- Which mixture of Blapple juice tastes most strongly of blueberry? (ratios 5:3 for Mixture A and 4:4 for Mixture B)
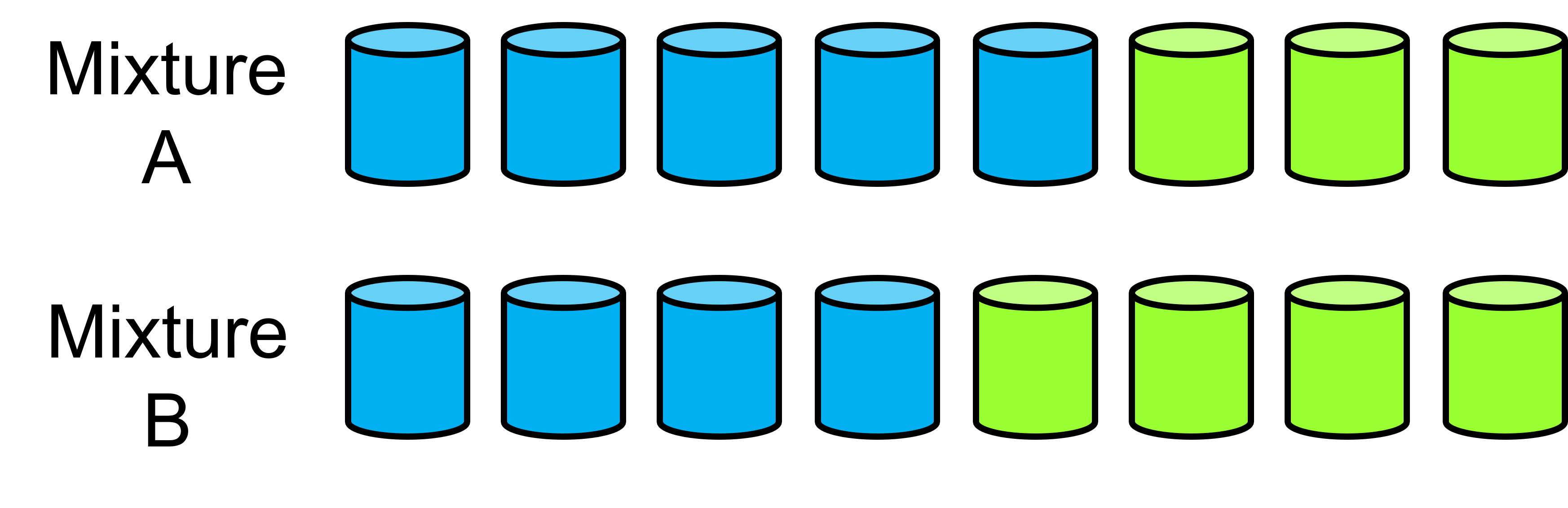
Explain how you know.
Signs of fluency and understanding:
Recognises that the number of units in the whole is the same (8 units). Therefore, Mixture A has the strongest flavour of blueberry. Explains that the fraction of blueberry in Mixture A is five eighths which is larger than the fraction of blueberry in Mixture B (four eighths or one half).
What to notice if your student does not solve the problem fluently:
Believes that Mixture A has a stronger blueberry flavour than Mixture A based on the numbers of units that are blueberry, rather than any reference to fractions. This may suggest that the student is relying on whole numbers. This may interfere with their comparison of ratios that are more complicated.
Supporting activity:
Comparing ratios with a common whole
- Which mixture of Blapple juice tastes most strongly of blueberry? (ratios 4:5 for Mixture A and 4:6 for Mixture B)
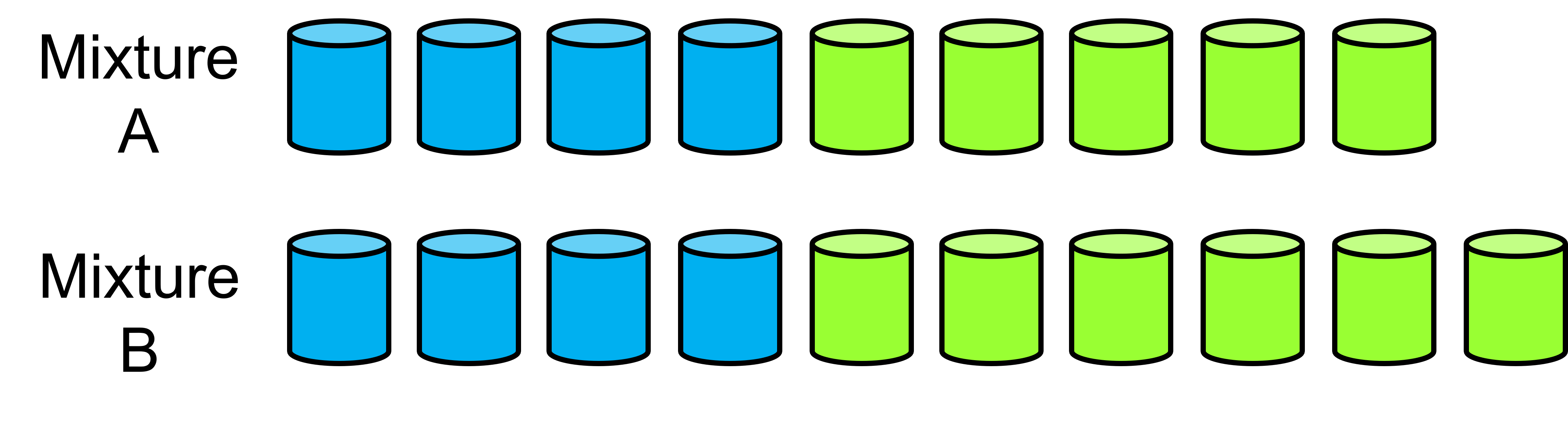
Explain how you know.
Signs of fluency and understanding:
Recognises that the number of blueberry units is the same in both mixtures (4 units). Therefore, Mixture A has the strongest flavour of blueberry because there are less units of apple to ‘balance’ the blueberry. Explains that the fraction of blueberry in Mixture A is four ninths which is a larger number than four tenths, the fraction of blueberry in Mixture B.
What to notice if your student does not solve the problem fluently:
Believes that both mixtures have the same flavour of blueberry because they both have four units of blueberry. This may suggest that the student is relying on whole numbers and not thinking of the part-whole relations as fractions. The student may need practical experience with mixing ratios to support them realise the attribute (strength of flavour) reflects the relationship between the parts and between the parts and the whole.
Believes that Mixture B is not as strong in blueberry flavour because it has six units of apple while Mixture A has only five units of apple. This may also indicate that the student is relying on whole numbers.
Supporting activity:
Comparing ratios with a common part
- Which mixture of Blapple juice tastes most strongly of blueberry? (ratios 3:5 for Mixture A and 2:3 for Mixture B)
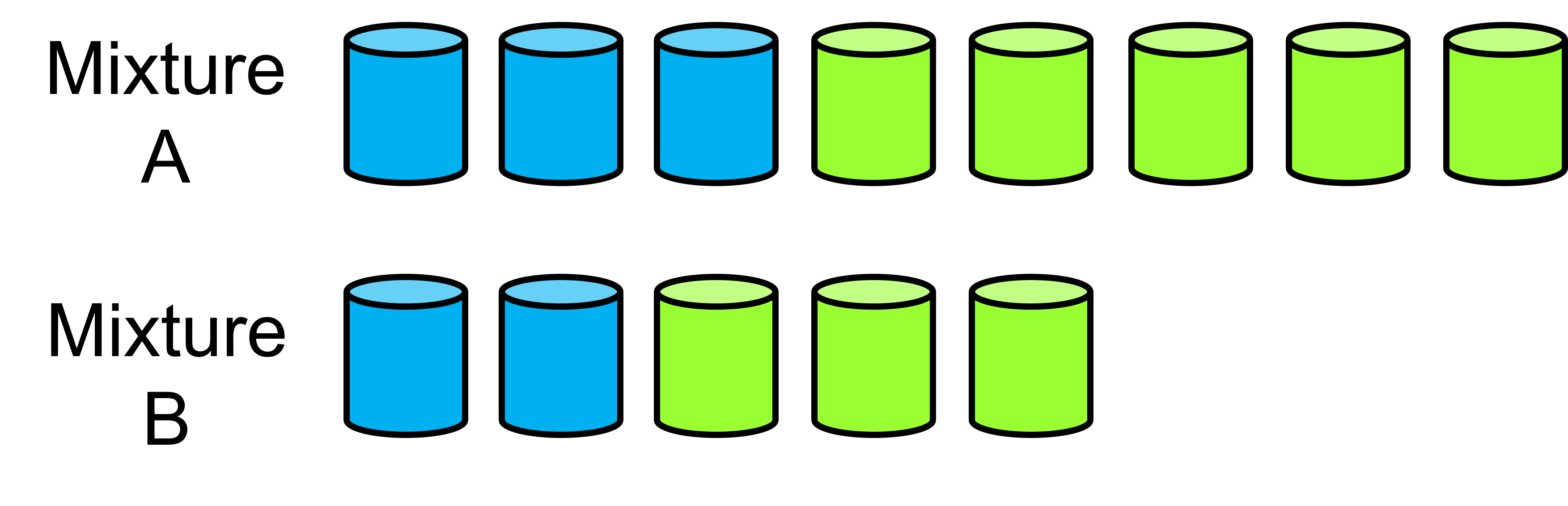
Explain how you know.
Signs of fluency and understanding:
Uses fractions to measure the strength of blueberry flavour in both mixtures. Calculates these fractions as three eighths for Mixture A and two fifths for Mixture B. Compares the fractions as numbers and concludes that Mixture B has a stronger blueberry taste because two fifths is a greater number than three eighths. The student may use decimals or percentages to compare the fractions, e.g. 2/5 = 40% and 3/8 = 37.5%.
What to notice if your student does not solve the problem fluently:
Believes that Mixture A has the strongest blueberry flavour since it has three units of blueberry compared to Mixture B that has only two units. This indicates that the student relies on whole number thinking and compares ratios using only one of the measures. The student needs support in finding the part-whole fractions in ratios.
Attempts to copy the ratios until a common part or whole is found. For example, replicates 2:3 to create 4:6 then 6:9 (Mixture B), and 3:5 to create 6:10 (Mixture A). Concludes that Mixture B is strongest since the number of parts for blueberry is the same, but Mixture B has only nine parts apple, compared to ten parts for Mixture A. This is a legitimate strategy but indicates that the student needs to develop a more efficient strategy that relies more on comparison of fractions.
Supporting activity:
Comparing ratios
Teaching activities
