New Zealand Curriculum: Level 3
Learning Progression Frameworks: Multiplicative thinking, Signpost 6 to Signpost 7
Target students
These activities are intended for students who have some previous experience of equal partitioning, such as finding lines of symmetry in shapes. It is preferable that they are also able to call on and apply their knowledge of addition and multiplication facts.
The following diagnostic questions indicate students’ understanding of, and ability to apply fractions as multipliers operating on other numbers. At this level the multiplicand (second factor) is restricted to whole numbers. The questions are given in order of complexity. If the student answers a question confidently and with understanding proceed to the next question. If not, then use the supporting activities to build and strengthen their fluency and understanding. Allow access to pencils and paper. You may also find it beneficial to support students, especially during the introduction of these types of questions, with sets of objects (e.g. counters), area models (e.g. fraction strips), and/or empty number lines. (show diagnostic questions)
The questions should be presented orally and in a written form so that the student can refer to them.
- Here are 18 counters. You can have one half of them. How many counters will you get?
Write an equation for this problem.
Signs of fluency and understanding:
Identifies nine as one half of 18, using either 2 x 9 = 18 or 9 + 9 = 18.
Records one of these equations: 1/2 x 18 = 9 or 2 x 9 = 18 or 18 ÷ 2 = 9.
May support their calculations with drawn diagrams or by physically grouping materials.
What to notice if your student does not solve the problem fluently:
Tries various numbers to see what works, such as 6 + 6 = 12 and builds on that result. This indicates that while the student may have knowledge of basic number facts, they a lack awareness of how to apply these. It might also demonstrate a lack of awareness of the connection between fractions, addition, and multiplication.
Relies on physically dealing the 18 counters between two people, then counts the result. This indicates a lack of awareness of the connection between fractions, addition, and multiplication, and demonstrates a need to develop further addition and multiplication basic facts knowledge.
Supporting activity:
Half as an operator
- Here are 24 counters. You can have three quarters of them. How many counters will you get?
Write an equation for this problem.
Signs of fluency and understanding:
Understands that three quarters means three of four quarters of equal size that make up the whole set of 24. Finds 1/4 of 24 by dividing 24 by four, or by using the corresponding multiplication fact, 4 x 6 = 24. Multiplies 3 x 6 = 18 to find three quarters.
Records 3/4 x 24 = 18.
What to notice if your student does not solve the problem fluently:
Unable to find three quarters. This may be due to lack of understanding of the fact that 3/4 = 1/4 + 1/4 + 1/4.
Using additive methods to find one quarter of 24, such as 5 + 5 + 5 + 5 = 20 so 6 + 6 + 6 + 6 = 24, and then 6 + 6 + 6 =18. Such strategies place considerable demand on working memory. The student may be unable to complete the strategy even with support of written recording. Use of these strategies may be due to lack of experience in using division and multiplication to find fractional parts.
Errors in calculations that are based on multiplication and division may be due to lack of basic fact knowledge.
Difficulties in recording the equation using a fraction as 3/4 x 24 = 18. This may be due to a lack of awareness that the multiplication symbol can be used to mean ‘of’, and may reflect limited transfer of whole number understanding of operations to the same operations with fractions.
Supporting activity:
Non unit fractions as operators
- Here are 42 counters. You can have five sevenths of them. How many counters will you get?
Write an equation for this problem.
Signs of fluency and understanding:
Understands that five sevenths as five of seven equally sized groups that make the whole set of 42. Finds 1/7 of 42 using division by seven, or a corresponding multiplication fact, 7 x 6 = 42. Multiplies 5 x 6 = 30 to find five sevenths.
Records 5/7 x 42 = 30.
What to notice if your student does not solve the problem fluently:
Unable to find five sevenths. This may be due to lack of understanding of the fact that 5/7 = 1/7 + 1/7 + 1/7 + 1/7 + 1/7
Using additive methods to find one seventh, such as 5 + 5 + 5 + 5 + 5 + 5 + 5 = 35 so 6 + 6 + 6 + 6 + 6 + 6 + 6 = 42. This strategy places considerable demand on working memory. The student may be unable to complete the strategy even with support of written recording. Use of these strategies may be due to lack of experience in using division and multiplication to find fractional parts.
Errors in calculations that are based on multiplication and division may be due to lack of basic fact knowledge.
Difficulties in recording the equation using a fraction as 5/7 x 42 = 30. This may be due to a lack of awareness that the multiplication symbol can be used to mean ‘of’, and may reflect limited transfer of whole number understanding of operations to the same operations with fractions.
Supporting activity:
Complex non-unit fractions as operators
- Here are 36 counters. You can have two-thirds of the counters or six-ninths of the counters. Which fraction gives you the most counters? Explain why.
Write equations for this problem.
Signs of fluency and understanding:
Understands that two thirds and six ninths are equivalent fractions. Therefore the numbers of counters for both fractions are the same. 2/3 x 36 = 6/9 x 36.
Calculates both amounts using multiplication and division, 2/3 x 36 = 24 and 6/9 x 36 = 24, then recognises that the fractions are equivalent.
What to notice if your student does not solve the problem fluently:
Unable to find two thirds of 36 or six ninths of 36. This may be due to lack of understanding of the fact that 2/3 = 1/3 + 1/3 and 6/9 = 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9. This lack of understanding should show in earlier questions. Inability to write equations for the problem should also have occurred in previous problems.
Attempts additive methods to find the fractional parts. The demands on working memory will make such strategies difficult even with support of written recording.
Errors in calculations that are based on multiplication and division may be due to lack of basic fact knowledge.
Inability to recognise 2/3 and 6/9 as equivalent fractions may be due to limited understanding of fractions as numbers.
Difficulties in recording equations using a fraction - 2/3 x 36 = 24 and 6/9 x 36 = 24. This may be due to a lack of awareness that the multiplication symbol can be used to mean ‘of’, and may reflect limited transfer of whole number understanding of operations to the same operations with fractions.
Supporting activity:
Equivalent fractions as operators
- Here is a rectangle of paper. If you get one quarter of one third of the paper, how much of the whole rectangle do you get? Explain how you know.
Write an equation for this problem.
Signs of fluency and understanding:
Recognises that the answer is one twelfth, using 3 x 4 = 12, and records ¼ x 1/3 = 1/12 or 1/3 x 1/4 = 1/12.
Explains that making quarters creates four equal parts and dividing each part into thirds creates 4 x 3 = 12 equal parts, twelfths.
These strategies may be supported by the use of diagrams or physical manipulation of materials (e.g. folded paper - see below).
What to notice if your student does not solve the problem fluently:
Draws a diagram or folds the paper to model the problem. This indicates that the student has yet to develop anticipation of the result (a scheme). The student may also experience difficulties in counting the fractional parts created - indicating a lack of unawareness of how to identify partitioned parts of fractions. The additional cognitive load needed to keep track of the parts of such a model may also make this strategy prohibitive.
Difficulties in recording an equation to represent this situation may indicate limited exposure to using the multiplication symbol to represent ‘of’ when both factors are fractions.
Supporting activity:
Unit fraction of a unit fraction
- Here is a rectangle of paper. Imagine I fold the paper into fifths width-ways and shade four fifths. (Demonstrate if necessary and write down the fractions).
Then I fold the paper into thirds length-ways. I shade two thirds of four fifths. What fraction of the rectangle is double shaded?
Write an equation for this problem.
Signs of fluency and understanding:
Recognises the problem as multiplication and records 2/3 x 4/5 = 8/15. Explains that the answer, 8/15, is two thirds or four fifths of the rectangle.
What to notice if your student does not solve the problem fluently:
Recognises the problem as multiplication and records 2/3 x 4/5 = [ ] but is unable to complete the procedure. That indicates the need for fluency with fraction multiplication algorithms.
Is unsure about the operation to perform on 2/3 and 4/5, and most commonly chooses addition or subtraction. This indicates that the student has not yet made the connection between ‘of’ and multiplication then the factors are fractions.
Draws a diagram to model the problem. This shows the student has yet to develop anticipation of the result (a scheme). Similarly they may fold the paper and shade it to get an answer. May or may not be able to recognise the double shaded area as 8/15 of the rectangle.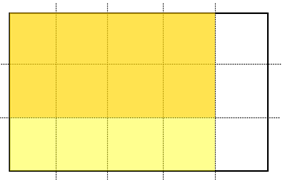
Difficulties in recording an equation to represent this situation may indicate limited exposure to using the multiplication symbol to represent ‘of’ when both factors are fractions.
Supporting activity:
Non-unit fraction of a non-unit fraction
Teaching activities
- Half as an operator
- Non unit fractions as operator
- Complex non-unit fractions as operator
- Equivalent fractions as operator
- Unit fraction of a unit fraction
- Non-unit fraction of a non-unit fraction