New Zealand Curriculum: Level 3
Learning Progression Frameworks: Multiplicative thinking, Signpost 6 to Signpost 7
Target students
These activities are intended for students who have some previous experience with equal partitioning, such as finding lines of symmetry in shapes. It is preferable that they have some knowledge of addition and multiplication facts.
The following diagnostic questions indicate students’ understanding of, and ability to locate fractions in relation to whole numbers and other simple fractions. A number line is used to find out students’ understanding about the size of fractions in relation to other numbers. The questions are given in order of complexity. If the student answers a question confidently and with understanding proceed to the next question. If not, use the supporting activities to build and strengthen their fluency and understanding. Allow access to pencil and paper. (show diagnostic questions)
The questions should be presented orally and in a written form so that the student can refer to them.
- Here is a number line showing zero and one. (Ensure that one is not at the end of the line.)
Mark where these fractions are on the number line and write the fractions underneath the mark. (Say the fractions one at a time rather than write the symbols)
One half, one quarter, one eighth
Signs of fluency and understanding:
Locates the correct position of each fraction by halving the spaces. Shows understanding that all fractions are located with reference to one, and the length between zero and one. Uses correct symbols to name the fractions.
What to notice if your student does not solve the problem fluently:
Locating one half at the half-way point of the line, instead of half-way between zero and one. This may indicate that the student does not yet understand that the size of fractions is determined with reference to one.
Inaccurate placement of the fractions, with limited use of halving, may indicate that the student does not yet understand that fractions of one involve equal parts.
Supporting activities:
Unit fractions
- Here is a number line showing zero and one. (Ensure that one is not at the end of the line.)
Mark where these fractions are on the number line and write the fractions underneath the mark. (Say the fractions one at a time rather than write the symbols)
One half, one third, one quarter, one fifth
Explain why you put the fractions in that order.
If the student replies “Because one third is less than one half, etc.” ask, Why is one third smaller?
Signs of fluency and understanding:
Locates the correct position of each fraction, using equal partitioning of spaces. Shows understanding that all fractions are located with reference to one, the length between zero and one. Uses correct symbols to name the fractions.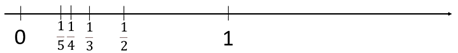
Explains the order of fractions, using an argument like “the more equal parts one is divided into, the smaller the equal parts are. For example, thirds are three equal parts and halves are two equal parts.”
What to notice if your student does not solve the problem fluently:
Inaccurate placement of fractions whilst writing correct fraction symbols. This indicates that the student may need to work on equal partitioning, using length and other physical models.
Difficulty locating and writing any fractions suggests that the student has yet to associate the words for common fractions with symbols or a length model of relative size.
Locating the fractions in opposite order suggests that the student has yet to understand that dividing the same one into more equal parts results in smaller equal parts. It is also likely that the student relies on whole number thinking, concentrating on the denominators (bottom numbers).
Supporting activities:
More unit fractions
- Here is a number line showing zero and one. (Ensure that one is not at the end of the line.)
Mark where these fractions are on the number line and write the fractions underneath the mark. (Say the fractions one at a time rather than write the symbols)
Three quarters, one third, five eighths
Explain why you put the fractions in the positions you did.
Signs of fluency and understanding:
Locates the correct position of each fraction, using equal partitioning of spaces and iteration of unit fractions. For example, three quarters is found by measuring three units of one quarter. Uses correct symbols to name the fractions.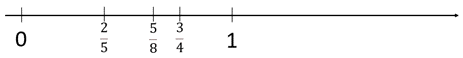
Explains the order of fractions, using a justification like “First I found one fifth then I put two fifths together.”
What to notice if your student does not solve the problem fluently:
Inaccurate but approximately correct placement of fractions whilst writing correct fraction symbols. This indicates that the student may need to work on equal partitioning of length and other physical models.
Difficulty locating and writing any fractions. This suggests that the student has yet to associate the words for non-unit fractions with symbols or a length model of relative size.
Locating the fractions incorrectly by attending to numerators only, 2/5 < 3/4 < 5/8, or denominators only, 3/4 < 2/5 < 5/8. This indicates the student has yet to learn the meaning of the numerators, as a count, and denominator as the size of parts.
Use of ‘gap thinking’ by finding the difference between denominator and numerator, giving an incorrect order of 5/8 = 2/5 < 3/4. This suggests that the student is applying the meaning of numerators and denominators. Gap thinking involves finding the number of parts less than one and is not a reliable strategy unless the size of parts is also considered.
Supporting activity:
Non-unit fractions
- Here is a number line showing zero and one. (Ensure that one is located about one third of the length from zero to the end of the line.)
Mark where these fractions are on the number line and write the fractions underneath the mark. (Say the fractions one at a time rather than write the symbols)
Five fifths, three halves, seven quarters, six thirds, nine eighths
Explain why you put the fractions in the positions you did.
Signs of fluency and understanding:
Locates the correct position of each fraction, using equal partitioning of spaces and iteration of unit fractions. Knows that five fifths equals one, and six thirds equals two. Subsequently, seven quarters is found by measuring seven units of one quarter or by finding one quarter less than two. Uses correct symbols to name the fractions.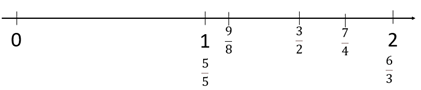
Explains the order of fractions, using a justification like “First I found one fifth then I put two fifths together.”
What to notice if your student does not solve the problem fluently:
Inaccurate but approximately correct placement of fractions whilst writing correct fraction symbols. This indicates that the student may need to work on equal partitioning of length and other physical models.
Difficulty locating and writing any fractions. This suggests that the student has yet to recognise that fractions can be equal or greater than one. It may also indicate a lack of understanding of how to integrate fractions with a number line showing whole numbers.
Inverting fractions is common when they are presented in symbolic form but is less likely to occur in spoken form. For example, treating 7/4 as 4/7 is an indication that the student has incorrectly generalized that the numerator is always less than the numerator. This may be a sign that they view fractions as “x out of y”.
Supporting activity:
Improper fractions
- Here is a number line showing zero and one. (Ensure that one is located about half-way along the length from zero to the end of the line.)
Mark where these fractions are on the number line and write the fractions underneath the mark. (Show the fractions in symbol form)
1/2, 3/4, 4/8, 2/5, 4/10, 9/12
Explain why you put the fractions in the positions you did.
Signs of fluency and understanding:
Locates equivalent fractions in the correct positions, using equal partitioning of spaces and the iteration of unit fractions, and/or relationships to trusted benchmarks like one half and one. For example, recognises that the numerator and denominator in two fifths can be doubled to create four tenths.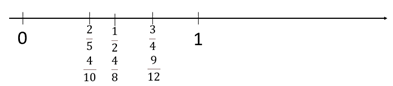
Explains the location of fractions, using a justification like “Three quarters and nine twelfths are equivalent fractions so they go in the same place.”
What to notice if your student does not solve the problem fluently:
Locating equivalent fractions in different positions. This may indicate that the student relies on measurement to locate each fraction individually and does not recognise equivalence.
Partial attempts at locating equivalent fractions, such as one half and four eighths in the same position, whilst providing an incomplete answer. This may be due to an absence of common factor knowledge.
Supporting activity:
Equivalent fractions