New Zealand Curriculum: Level 3
Learning Progression Frameworks: Multiplicative thinking, Signpost 4 to Signpost 5
Target students
These activities are intended for students who understand multiplication as the repeated addition of equal sets, and who have some knowledge of basic multiplication facts.
The following diagnostic questions indicate students’ understanding of, and ability to apply division to situations that involve repeated equal subtraction. The questions are given in order of complexity. If the student answers a question confidently and with understanding proceed to the next question. If not, use the supporting activities to build and strengthen their fluency and understanding. Allow access to pencil and paper but not to a calculator unless stated. (show diagnostic questions)
The questions should be presented orally and in a written form so that the student can refer to them. The questions have been posed using a people (represented by counters) context. This can be changed to other contexts that are engaging to your students, such as Lego™, smarties, novelty counters, or toy vehicles.
- Here are 12 boys and girls. (Show student the 12 counters).
They need to get themselves into pairs. How many pairs will there be?
(Ask for a prediction before letting the student equally share the counters into six sets of two. Physically modelling the situation is not needed if the student responds quickly.)
Signs of fluency and understanding:
Anticipates that 12 people can form six pairs, using basic fact knowledge, such as 6 + 6 = 12 (additive) or 6 x 2 = 12 (Multiplicative).
What to notice if your student does not solve the problem fluently:
Forms pairs, using two counters each time, to establish the number of pairs. This is a sign that the student does not yet anticipate the result. Lack of anticipation may be due to inadequate number fact knowledge. It may also stem from not recognising the opportunity to apply addition or multiplication knowledge. Division as equal subtraction should meet these criteria:
- All the objects are distributed (exhausted)
- The correct size of parts is used (two people in each pair)
- The number of parts is correct (six pairs)
Watch for students to recount or subitise the counters to check the pairs are equal. Recounting indicates a belief that validating equality is an integral part of the equal subtraction process.
Supporting activities:
Anticipating the result of equal subtraction (quotative division)
- Here are 20 people. (Show student the 20 counters).
They get into teams of four people. How many teams do they make?
Write an equation for what you have done. Can you write a division equation?
Signs of fluency and understanding:
Anticipates the number of teams, five, without physical modelling. Uses multiplication or division fact knowledge, such as 5 x 4 = 20 or 20 ÷ 4 = 5.
What to notice if your student does not solve the problem fluently:
One by one forming of four teams, whether physical or imaged. This suggests that the student is unaware that the result can be predicted. They may also lack the number fact knowledge required make the prediction.
Students' additive methods might include progressively trying addends, such as 4 + 4 + 4 = 12 then 12 + 4 = 16, then 16 + 4 = 20. This creates additional memory load, as students must keep track of the number of fours that are created. These methods indicate the student has yet to connect multiplication with equal addition, and/or lacks multiplication facts to apply.
Supporting activities:
Using multiplication facts to anticipate equal subtraction (quotative division)
- Here are 18 people. (Show student the 18 counters).
A car can take 3 people. How many cars do you need to take all the people to the show?
(Ask for a prediction then let the student use materials to form sets of three, if needed. Do not physically share if the response is fluent and correct)
Write a division equation for what you have done.
Signs of fluency and understanding:
Anticipates the number of equal sets of three fluently without physical modelling. Uses multiplication or division fact knowledge, such as 6 x 3 = 18 or 18 ÷ 3 = 6. Represents the operation as 18 ÷ 3 = 6.
What to notice if your student does not solve the problem fluently:
Repeatedly creating sets of three, whether physical or imaged. This suggests that the student is unaware that the result can be predicted using number facts. They may also lack the number fact knowledge required make the prediction.
Students' additive methods might include progressively adding threes and may include a trusted fact, such as 3 + 3 + 3 = 9, then building up until all 18 people are used. These methods indicate the student has yet to fully connect multiplication with equal addition. They may also lack the required multiplication facts to apply, in this case multiples of three.
Inability to write a division fact may indicate that the student does not connect repeated equal subtraction with division.
Supporting activities:
Using division facts to anticipate the result of repeated subtraction
- There are 54 players. They get into teams of six for a volleyball tournament. How many teams do they make?
(Avoid modelling the problem physically. Look for students to use mental or written strategies)
Write a division equation for this problem.
Signs of fluency and understanding:
Anticipates the number of equal teams using mental or written strategies. Uses multiplication or division fact knowledge, such as 9 x 6 = 54 or 54 ÷ 6 = 9. Represents the operation as 54 ÷ 6 = 9.
Anticipates the number of teams fluently by deriving from a known multiplication or division fact, such as 10 x 6 = 60 so 9 x 6 = 54.
What to notice if your student does not solve the problem fluently:
Students' additive methods might include progressively adding sixes until the target of 54 is reached, such as 6 + 6 = 12 (2 teams), 12 + 12 = 24 (4 teams), 24 + 24 = 48 (8 teams), 48 + 6 = 54 (9 teams). This creates additional memory load, as students must keep track of the number of sixes that are created. Additive methods indicate that the student relies on addition fact knowledge. They may also be unaware of, or unable to apply the connections between multiplication and equal addition.
Partial multiplication strategies might include using a known fact, such as 5 x 6 = 30 then building on additively. The heavy load on working memory makes these strategies prohibitive unless written recording is used.
Inability to write a division equation may indicate that the student needs opportunities to use the division sign to model repeated subtraction (quotative division) situations.
Supporting activities:
Creating facts to solve quotative division problems
- There are 120 people to take to the kapa haka festival. Each minibus takes 8 people. How many minibuses are needed?
(Avoid modelling the problem physically. Look for students to use mental or written strategies.)
Write a division equation for this problem.
Signs of fluency and understanding:
Uses an efficient place value based, multiplicative strategy to anticipate the number of minibuses needed (15). This might include:
- Applying the distributive property for multiplication, such as 8 x 10 = 80, 5 x 8 = 40, therefore 15 x 8 = 120.
- Applying proportional adjustment, such as 30 x 4 = 120 so 15 x 8 = 120 (this is a less likely strategy).
If the student uses a written algorithm, ask place value related questions to find out if they understand the meaning of the symbols, such as “Tell me where the ‘four’ came from and what it means.”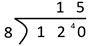
What to notice if your student does not solve the problem fluently:
Students' additive methods might include progressively adding eights such as 8 + 8 = 16 then 16 + 8 = 24, …etc. until 120 is reached. This indicates that the student relies on addition fact knowledge. They may also be unaware of, or currently unable to apply, the connections between multiplication and equal addition.
Partial multiplicative strategies might include the use of a known multiplication fact, in this case 10 x 8 = 80, followed by repeated addition until the target is reached.
Without the use of written recording, these additive and partial multiplicative strategies place additional load on working memory.
Inability to write a division equation indicates that the student needs opportunities to use the division sign to model repeated subtraction (quotative division) situations.
Supporting activities:
Apply place value to quotative division
Teaching activities
- Anticipating the result of equal subtraction (quotative division)
- Using multiplication facts to anticipate equal subtraction (quotative division)
- Using division facts to anticipate the result of repeated subtraction
- Creating facts to solve quotative division problems
- Applying place value to quotative division