Purpose:
You can help your child to use physical materials to represent multiplication equations.
What you need:
- A collection of shells (or leaves)
- Pencil and paper
- Written multiplication and division equations (PDF, 22KB)
What to do:
Play this game with your child.
For example:
 2 x 5 = 10 2 rows/groups of 5 = 10 |
 4 x 3 = 12 4 rows/groups of 3 = 12 |
 5 x 4 = 20 5 rows/groups of 4 = 20 |
Questions and further challenges
Consider this. One person has made:

This represents 4 x 3 = 12 because 4 groups, or rows of three, is 12 shells altogether.
What if this card is turned over? 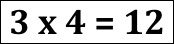
Discuss that you can look at this arrangement (array) from the side and see 3 x 4 = 12

(This is called the commutative property of multiplication but your child is not expected to know this.)
Decide whether you are happy to accept both equations 4 x 3 = 12 and 3 x 4 = 12 and discuss why.
As you play the game, add a further challenge. If a player has an array and an equation that match, they are required to also write a division problem that the shell arrangement also shows.
For example:

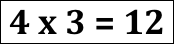
This person would record 12 ÷ 4 = 3 and explain “When I divide 12 shells into 4 equal groups, there are three in each group.”
What to expect your child to do:
- Correctly read multiplication equations.
- Understand and be able to represent a multiplication equation with materials.
- Write a division equation to correctly represent an array of shells.
He Kupu Māori:
|
whakarea |
multiplication |
|
ōrite |
equal |
|
whakawehe |
division |
Download a file of this activity:
PDF (538KB)