The purpose of this unit is to engage students in applying their understanding of measurement and algebra in investigating a physical system.
- Solve problems involving the conservation of mechanical energy.
- Find elastic potential energy using graphs.
- Determine the nature of the relationship between physical quantities (height and elastic stored energy) using a graph.
- Use a physical property, elastic potential energy, to find an unknown quantity.
Students will apply their understanding of measurement and algebraic skills through investigating the conservation of mechanical energy in the context of catapults.
The SI units of measurement have been used throughout this unit ensure validity of the physical relationships used in calculations. Students may be more comfortable measuring with derived units such as mm or cm, but should be encouraged to convert these measurements into SI units, such as the m, to ensure clear and accurate mathematical communication.
This cross-curricular, context-based unit aims to deliver mathematics learning, whilst encouraging differentiated, student-centred learning.
The learning opportunities in this unit can be further differentiated by providing or removing support to students, and by varying the task requirements. Ways to differentiate include:
- roaming and supporting students in a variety of groupings to ensure they understand the task at hand, the skills needed to succeed, and can apply these skills in a suitable process
- varying the amount of structured scaffolding and guided teaching you provide to students when investigating new tasks
- providing opportunities for students to create their own problems related to a relevant context
- providing extended opportunities for students to revise and apply learning from throughout the unit
- modelling the application of ideas at every stage of the unit
- strategically organising students into pairs and small groups in order to encourage peer learning, scaffolding, and extension
- allowing access to calculators to decrease the cognitive load required in each stage of the unit
- working alongside individual students (or groups of students) who require further support with specific areas of knowledge or activities.
With student interest engaged, mathematical challenges often seem more approachable than when presented in isolation. Therefore, you might find it appropriate to adapt the contexts presented in this unit.
Structure
The first session is an introductory activity that is aimed to spark the imagination of students, to introduce the need for a particular idea or technique in mathematics that would enable them to explore deeper into that context. It is expected that rich discussion may be had around the context and around the nature of the mathematics involved.
Following the introductory session, each subsequent session in the unit is composed of four sections: Introducing Ideas, Building Ideas, Reinforcing Ideas, and Extending Ideas.
Introducing Ideas: It is recommended that you allow approximately 10 minutes for students to work on these problems, either as a whole class, in groups, pairs, or as individuals. Following this, gather the students together to review the problem and to discuss ideas, issues and mathematical techniques that they noticed during the process. It may be helpful to summarise key outcomes of the discussion at this point.
Building Ideas, Reinforcing Ideas, and Extending Ideas: Exploration of these stages can be differentiated on the basis of individual learning needs, as demonstrated in the previous stage of each session. Some students may have managed the focus activity easily and be ready to attempt the reinforcing ideas or even the extending ideas activity straight away. These could be attempted individually or in groups or pairs, depending on students’ readiness for the activity concerned. The students remaining with the teacher could begin to work through the building ideas activity together, peeling off to complete this activity and/or to attempt the reinforcing ideas activity when they feel they have ‘got it’.
It is expected that once all the students have peeled off into independent or group work of the appropriate selection of building, reinforcing and extending activities, the teacher is freed up to check back with the ‘early peelers’ and to circulate as needed.
Importantly, students should have multiple opportunities to, throughout and at the conclusion of each session, compare, check, and discuss their ideas with peers and the teacher, and to reflect upon their ideas and developed understandings. These reflections can be demonstrated using a variety of means (e.g. written, digital note, survey, sticky notes, diagrams, marked work, videoed demonstration) and can be used to inform your planning for subsequent sessions.
The relevance of this learning can also be enhanced with the inclusion of key vocabulary from your students' home languages. For example, te reo Māori kupu such as koki (angle), teitei (altitude, height, high, tall), rahi (quantity), āhua (shape), tere whaiahu (velocity), kauwhata (graph), raraunga (data), papatipu (mass), and pānga rārangi (linear relationship) could be introduced in this unit and used throughout other mathematical learning.
Introductory Activity
The aim of this activity, which presents an opportunity to practise mathematical skills and knowledge in a science context, is to motivate students towards the context and to inform teachers of students' understandings.
- Have students investigate, using a rubber band, an eraser and a protractor, the path of a projectile launched from a slingshot. To replicate a slingshot, stretch a rubber band stretched between a splayed thumb and forefinger.
- What is the optimum firing angle of a slingshot to achieve the maximum height of the projectile?
- What is the optimum firing angle of a slingshot to achieve the maximum horizontal distance of the projectile?
As students work, observe their management of quantities. Use these observations to gauge your students' positions on the measurement sense learning progression.
- Discuss, drawing attention to the following points:
- Describe the shape of the path of the projectile.
- What factors other than the launch angle affected the distance the projectile would cover?
Session One
This session focuses on problem solving involving quantities that are defined by a physical property; the conservation of mechanical energy.
Introducing Ideas
- Introduce the following problem to students: A projectile is drawn back in slingshot, with elastic potential energy of 40 J.
- List and quantify the energy transformation present at the launch of the projectile.
Discuss, drawing attention to the following points:
- What are the types of energy present?
- Is mechanical energy conserved?
- Will there be further energy transformations during the flight of the projectile?
Building Ideas
Introduce the following context to students: A projectile is drawn back in a slingshot. The projectile is launched horizontally.
Provide time for students to do the following:
- Sketch the shape of the path of the projectile.
- Assuming there is no friction present, describe the energy forms present when the projectile falls to the height it was launched at.
Reinforcing Ideas
- Introduce the following context to students: A projectile is drawn back in a slingshot. The projectile is launched at an angle of 45° to the horizontal.
Provide time for students to do the following:
- Sketch the shape of the path of the projectile.
- Assuming there is no friction present, describe the energy forms present at the top of the path.
- Assuming there is no friction present, describe the energy forms present when the projectile falls to the height it was launched at.
Extending Ideas
- Introduce the following context to students: A projectile is drawn back in a slingshot, with elastic potential energy of 40 J. The projectile is launched at an angle of 45° to the horizontal.
- Provide time for students to label the diagram below. They should show how the initial velocity of the projectile has a horizontal speed equal to its vertical speed. Once it has been launched, assuming there is no friction present, the horizontal speed is constant. It is the vertical speed that changes because of the force due to gravity.
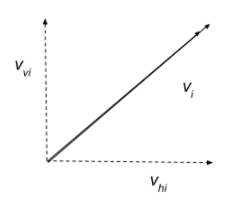
Provide time for students to do the following:
Use the conservation of energy to quantify the energy form(s) present at the top of the path.
Use the conservation of energy to quantify the energy form(s) present when the falling projectile is at the height at which it was launched.
Session Two
Introducing Ideas
- Introduce the following context to students: To find the amount of elastic potential energy that can be stored in a stretch rubber band, measure the extension (in m) of the band when various weights (in N) are hung from the band.
- Record your results in a table. You should have data for at least four different weights.
Discuss, drawing attention to the following points:
- How did you know the number of N of each mass? How does this differ from mass (in g or kg)?
- How did you measure the extension of the band?
- Does this relationship appear to be linear or non-linear?
- Would the point (0, 0) lie on the line/curve of this graph?
Building Ideas
Provide time for students to work through the following tasks:
- Graph the data collected in your investigation to find the relationship between weight (N) and extension (m) of the rubber band:
- Draw a set of positive axes occupying at least half a page of quad paper.
- Choose a suitable scale for the weight (N) that will use as much of the vertical axis as possible. Label that axis and mark on the scale in N.
- Choose a suitable scale for the extension (m) that will use as much of the horizontal axis as possible. Label that axis and mark on the scale in N.
- Plot the data you collected.
- Rule the line of best fit for your data.
- Describe the relationship shown by this graph.
Reinforcing Ideas
- Explain to students: The area under the Force (N) vs Extension (m) graph, from 0 m to a given extension, x gives the elastic potential energy stored when the spring or elastic is stretched by x.
Provide time for students to work through the following tasks:
- Construct a graph of the data from your investigation.
- Give the relationship shown by this graph
- The unit of energy is the joule, J. What is the equivalent to J in terms of the newton, N and the metre, m.
- Find the Elastic Potential Energy, in J, stored in the rubber band at the maximum extension.
Extending Ideas
Introduce the following context to students: The area under the Weight Force (N) vs Extension (m) graph, from 0 m to a given extension, x gives the elastic stored when the spring or elastic is stretched by x m.
Provide time for students to work through the following tasks, based on a graph of the results of their investigation:
- Write a general rule for the Elastic Potential Energy, Ee, stored in the rubber band in terms of the weight force suspended, F, and the amount of extension, x.
- Write a rule for the Elastic Potential Energy, Ee, stored in this rubber band in terms of only the amount of extension, x.
Session Three
Introducing Ideas
- Together, place a small projectile in a rubber band slingshot. Extend the rubber band by 5 cm. Launch the projectile vertically and estimate the height the projectile reaches. Repeat sufficient times to find an average height.
Discuss, drawing attention to the following points:
- How did you ensure accuracy in your measurement of the extension of the rubber band?
- How did you ensure accuracy in your measurement of the height reached by the projectile?
- How might you know that you had made a sufficient number of repeats for this investigation? (hint: The differences between mode, mean and/or median could be considered.)
Building Ideas
Introduce the following context to students: Gravitational potential energy, Ep in J, is calculated from the rule, Ep = mgh, where m is mass (in kg), h is height (in m) and g = 10 ms-2.
Provide time for students to work through the following tasks:
- Measure the mass of the small projectile that you are using in your investigation.
- Use the results of your investigation to find the gravitational potential energy gained by the projectile when the slingshot was extended by 5 cm.
- Estimate the elastic potential stored by the slingshot when it was extended by 5 cm.
Reinforcing Ideas
Introduce the following context to students: Gravitational potential energy, Ep in J, is calculated from the rule, Ep = mgh, where m is mass (in kg), h is height (in m) and g = 10 ms-2.
Provide time for students to work through the following tasks:
- Investigate to find the height the projectile reaches when the rubber band is extended by 10 cm and the slingshot is aimed vertically.
- Use the results of your investigation, and the mass of the projectile, to find the gravitational potential energy gained by the projectile when the slingshot was extended by 10 cm.
- Estimate the elastic potential stored by the slingshot when it was extended by 10 cm.
Extending Ideas
Introduce the following context to students: Gravitational potential energy, Ep in J, is calculated from the rule, Ep = mgh, where m is mass (in kg), h is height (in m) and g = 10 ms-2. The mass of the projectile can be measured with a mass balance.
Provide time for students to work through the following tasks:
- Find the height reached by a projectile launched from a vertical slingshot, with the rubber band extended 3 cm, 6 cm and 9 cm.
- Find the gravitational potential energy gained by a projectile launched from a vertical slingshot, with the rubber band extended 9 cm.
- Find the elastic stored energy provided by a projectile launched from a vertical slingshot, with the rubber band extended 9 cm.
- Is the relationship between the elastic stored energy in the slingshot and the height reached by the projectile a linear or a non-linear relationship? Justify your answer.
Session Four
- Together, measure, as accurately as possible, the maximum height a projectile will go when launched by a rubber band slingshot extended 2 cm, 4 cm, 6 cm, 10 cm.
- Do these data indicate a linear or a non linear relationship between extension and maximum height reached?
Discuss, drawing attention to the following points:
- How did you organise the recording/display of your data?
- How did the way you organised your data assist your conclusion about whether or not the relationship is linear?
Building Ideas
Provide time for students to graph the data collected in their investigations, following the process described below, and to find the relationship between height reached (m) and extension (m) of the rubber band.
- Draw a set of positive axes occupying at least half a page of quad paper.
- Choose a suitable scale for the height reached (m) that will use as much of the horizontal axis as possible. Label that axis and mark on the scale in decimal values of m.
- Choose a suitable scale for the extension (m) that will use as much of the horizontal axis as possible. Label that axis and mark on the scale in decimal values of m.
- Plot the data you collected.
- Is the relationship shown linear?
Reinforcing Ideas
Provide time for students to work through the following tasks:
- Construct a graph of height reached (m) of the projectile against extension (m) of the rubber band.
- Draw in the curve of best fit for your data.
- Describe the relationship shown by this graph as linear or non-linear.
Extending Ideas
Provide time for students to graph their data and describe the relationship shown by their graph (i.e. as linear or non-linear).
Provide time for students to work through the following tasks:
- Use your graph to predict the height a projectile will reach when the rubber band is extended by 8 cm.
- Test your prediction.
- Comment on the similarities/differences between your predicted and tested heights.
Session Five
Introducing Ideas
Introduce the following context to students: The elastic potential energy of a rubber band slingshot depends on the extension of the rubber band by the rule: Ee = ½ kx2.
- What shape will the graph of elastic potential energy against extension form? (nb k is a constant for a given spring or rubber band).
Discuss, drawing attention to the following points:
- Could you answer this question by inspection of the rule? What clues did it give about the shape of the graph?
- Could you answer this question by testing various values of x? Would you need to assign a value for k?
Building Ideas
Introduce the following context to students: The elastic potential energy stored by extending a slingshot of extension, x, is described by the equation Ee = ½ kx2.
Provide time for students to work through the following tasks:
- Find the elastic potential energy that is stored in a slingshot of k = 40 N/m extended by 0.075 m.
- Find the elastic potential energy that is stored in a slingshot of k = 40 N/m extended by 0.15 m.
- What was the effect on the amount of elastic potential energy of doubling the extension of a slingshot?
Reinforcing Ideas
Introduce the following contexts to students:
The elastic potential energy stored by extending a slingshot of extension, x, is described by the equation Ee = ½ kx2.
The gravitational potential energy gained by the projectile at the top of its path is described by the equation Ep = mgh.
Provide time for students to work through the following tasks:
- Use the conservation of energy to find an expression for h, the height the projectile will reach, in terms of k, x, m and g.
- Given that the quantities k and m are constant for this investigation and g is always a constant value, comment on the shape of the graph of h against x.
- Use your expression for h to find the height a 0.05 kg projectile will reach if launched from a slingshot of k = 30 Nm-1 that has been extended by 0.12 m. Use g = 10 ms-2.
Extending Ideas
Introduce the following contexts to students:
The elastic potential energy stored by extending a slingshot of extension, x, is described by the equation Ee = ½ kx2.
The gravitational potential energy gained by the projectile at the top of its path is described by the equation Ep = mgh.
Provide time for students to find what the effect would be on the height that a projectile reaches, if the extension of a given slingshot is doubled? Support them to justify their answers.
Dear parents and whānau,
We have recently applied our understanding of measurement and algebra in investigating a physical system. Ask your child to share their learning with you.