Purpose:
You can help your child to make common solid (three-dimensional) shapes and make paper/cardboard patterns for these, and to correctly identify prisms.
What you need:
- Play dough - click for recipe (PDF, 325KB)
- A plastic knife, or ‘safe’ kitchen knife
- Spare paper or cardboard
- Pencil, ruler and eraser
- Scissors
- Cellotape or glue
What to do:
-
Have your child use the dough to make and name a cube, a cylinder, a sphere, a cuboid (long cube or rectangular prism), a square based pyramid, a cone and a triangular prism.
-
Have your child talk to you about the distinguishing features of each shape, for example "The square based pyramid has 5 vertices (corners where 3 edges meet), 8 edges (where 2 ‘sides’ or faces meet), and 5 faces of which one is a square and 4 are triangles."
-
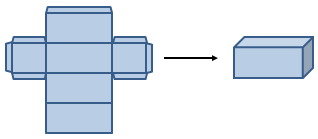
Have your child chose some of the shapes with straight edges, and using paper or card, make and cut a pattern for this shape. They should include tabs on their pattern so the shape can be folded and glued to make a three dimensional model. For example:
Have your child put their play dough shapes in the fridge while they cut out and glue/tape their paper/cardboard shapes together. Chilling the dough shapes will make them firmer and this will make the next task more successful. -
Now say, “I want you to slice at least twice through each play dough shape. But before you do, I want you to predict which shapes will have slices that are all the same size and shape, and which ones will have slices that are different sizes or shapes.”
-
Have them make their prediction and then have them slice through their play dough shapes to see if their predictions are correct.
NB. When a prism is sliced through, its slices are the same size shape, like this:
If you slice through a shape that is not a prism, eg, a pyramid, the slices will change shape and size.
So, a prism is a solid object that has two identical ends and all flat sides. The cross section is the same all along its length. -
Talk together about what has happened and together agree which shapes are prisms.
What to expect your child to do:
- Make and name common solid three-dimensional shapes.
- Make paper or cardboard patterns (nets) for common three-dimensional shapes.
- Identify features of prisms.
He Kupu Māori:
| play dough | poikere |
| shape | āhua |
| round | porotaka |
| straight | torotika |
| sharp, pointy | koi, whakakoikoi |
| curvy, bendy | kōpiko |
| flat | papatahi |
| cone | koeko |
| cube | mataono rite |
| corner, vertice | kokonga |
| edge | tapa |
| surface/face | mata |
| cone | koeko |
| cylinder | rango |
| sphere | poi |
| rectangular prism | poro tapawhā hāngai |
| pyramid | koeko tapawhā rite |
| triangular prism | poro tapatoru |
| net (of a 3 dimensional shape) | raumata |
He Whakawhitinga Kōrero:
- Hangaia tētahi mataono rite ki te poikere. (Make a cube from the play dough.)
- He aha ngā ingoa pāngarau mō ēnei āhua? (What are the maths names for these shapes?)
- Whakamāramatia mai te āhua o te koeko tapawhā rite. (Explain to me the shape of the cone.)
- He tapawhā rite te pūtake o tēnei āhua. E whā atu anō ngā mata, he tapatoru te āhua. Ka tūtaki ēnei mata ki te tihi o te koeko. (The base of this shape is a square. There are four other faces which are triangular. They meet at the point or apex of the pyramid.)
- E hia ngā kokonga o te …? (How many corners has the … got?)
- He torotika, he kōpiko rānei ngā tapa? (Are the edges straight or curved?)
- He ōrite te āhua me te rahi o ngā mata katoa. (The shape and size of all the faces are the same.)
- E rua ngā mata porowhita. (There are two circular faces.)
- Ka whakamahi tāua i te kāri mārō hei hanga i tētahi poro tapawhā hāngai. He papatahi te kāri, engari ka whētuia hei hanga i te poro. He rite ki te pouaka. Ka kīia tēnei he raumata. Koia nei te raumata hei hanga poro tapawhā hāngai. (Together we’re going to use some cardboard to make a rectangular prism. The carboard is flat but we can fold it to make the prism. It’ll be like a box. This is called a net. This is a net for making a rectangular prism.)
- Me pēhea te hanga raumata hei mahi i tētahi poro tapatoru? (How can we make a net to build a triangular prism?)
- E rua ngā pito o te poro tapatoru, he tapatoru te āhua. He tapawhā hāngai ngā mata e toru e hono ana i ēnei pito. (There are two ends of the triangular prism which are triangular shaped. The three faces which join these ends are a rectangular shape.)
- Mēnā ka tapahia te [poro tapatoru] ki konei, ka pēhea te āhua o te mata tapahi ka hua mai? (If we cut the triangular prism here, what will be the shape of the sliced surface?)
- Mēnā ka tapahia ki konei, ka ōrite anō te āhua o te mata tapahi, ka rerekē rānei? (If it is sliced here, will the sliced surface be the same or different?)
Download a file of this activity:
PDF (293KB)