This unit provides an opportunity for students to explore an integrated mathematics and science context: chemical reactions involving acids and bases. Within this, students develop their use of rates and ratios through exploration of linear relationships using tables and graphs. Students also develop their understanding of multiplicative thinking, and patterns and relationships in this context.
SI units of measure are used to provide concrete reinforcement of the knowledge and skills used in rates and ratios, and of the application of the gradient of a linear relationship to solve problems.
- use rates, ratios, and reasoning with linear proportions to solve a problem.
- make connections between representations of linear data in tables and graphs.
This unit provides an opportunity for students to solve problems using proportions described as a ratio or decimal value, and to solve problems involving rates. Within this, students will develop and apply their understanding of the multiplicative relationship between different rates and measures, scaling up or down as is appropriate to the situation given.
Students will also recognise a pattern, from a table and/or a graph and describe it as being linear (or not). They will plot a linear relationship on an appropriate set of axes and describe the key features of the graph, and will be encouraged to generalise the pattern, forming a rule from which predictions can be made and tested.
Note that the context of neutralising acids and bases does not yield the exact linear relationships hinted at in this unit, but does so approximately when only strong acids and bases are used. It can be argued that students will gain a better understanding of chemical processes overall, if they can first look for clear patterns in such constrained settings.
The practical work outlined in the introductory activity requires solutions and equipment that should be available in secondary school laboratories. You should have access to the expertise of a science teacher and the necessary resources to successfully deliver this unit of practical work.
This cross-curricular, context-based unit aims to deliver mathematics learning, whilst encouraging differentiated, student-centred learning.
The learning opportunities in this unit can be further differentiated by providing or removing support to students, and by varying the task requirements. Ways to differentiate include:
- roaming and supporting students in a variety of groupings to ensure they understand the task at hand, the skills needed to succeed, and can apply these skills in a suitable process
- varying the amount of structured scaffolding and guided teaching you provide to students when investigating new tasks
- providing opportunities for students to create their own problems
- providing extended opportunities for students to revise and apply learning from throughout the unit
- modelling the application of ideas at every stage of the unit
- strategically organising students into pairs and small groups in order to encourage peer learning, scaffolding, and extension
- working alongside individual students (or groups of students) who require further support with specific areas of knowledge or activities (e.g. forming solutions).
Note that this unit is focussed on exploring rates, ratios, and linear relationships in an integrated mathematics and science context: chemical reactions involving acids and bases. As such, it is not set in a real world context. You may wish to explore real world applications of this context in teaching sessions following the unit.
Structure
The first session is an introductory activity that is aimed to spark the imagination of students, to introduce the need for a particular idea or technique in mathematics that would enable them to explore deeper into that context. It is expected that rich discussion may be had around the context and around the nature of the mathematics involved.
Following the introductory session, each subsequent session in the unit is composed of four sections: Introducing Ideas, Building Ideas, Reinforcing Ideas, and Extending Ideas. Note that sessions one, two, three, and six have the same focus (on students using rates, ratios, and reasoning with linear proportions to solve a problem), as do sessions four and five (on students relating a linear pattern, shown in a table, to a graph displaying the same data).
Introducing Ideas: It is recommended that you allow approximately 10 minutes for students to work on these problems, either as a whole class, in groups, pairs, or as individuals. Following this, gather the students together to review the problem and to discuss ideas, issues and mathematical techniques that they noticed during the process. It may be helpful to summarise key outcomes of the discussion at this point.
Building Ideas, Reinforcing Ideas, and Extending Ideas: Exploration of these stages can be differentiated on the basis of individual learning needs, as demonstrated in the previous stage of each session. Some students may have managed the focus activity easily and be ready to attempt the reinforcing ideas or even the extending ideas activity straight away. These could be attempted individually or in groups or pairs, depending on students’ readiness for the activity concerned. The students remaining with the teacher could begin to work through the building ideas activity together, peeling off to complete this activity and/or to attempt the reinforcing ideas activity when they feel they have ‘got it’.
It is expected that once all the students have peeled off into independent or group work of the appropriate selection of building, reinforcing and extending activities, the teacher is freed up to check back with the ‘early peelers’ and to circulate as needed.
Importantly, students should have multiple opportunities to, throughout and at the conclusion of each session, compare, check, and discuss their ideas with peers and the teacher, and to reflect upon their ideas and developed understandings. These reflections can be demonstrated using a variety of means (e.g. written, digital note, survey, sticky notes, diagrams, marked work, videoed demonstration) and can be used to inform your planning for subsequent sessions.
The relevance of this learning can also be enhanced with the inclusion of key vocabulary from your students' home languages. For example, te reo Māori kupu such as pāpātanga (rate), ōwehenga (ratio), and pānga rārangi (linear relationship) might be introduced in this unit and then used throughout other mathematical learning.
- a rack of 5 test tubes
- droppers or pipettes
- universal indicator
- a universal indicator colour chart giving the whole number pH scale 1-14
- HCl (0.1 molL-1) and NaOH (0.1 molL-1) solutions, in beakers or bottles
- copies of the graphs featured throughout the unit
- table templates (optional - your students might construct these themselves).
Session One
The aim of this session to motivate students towards the context and to inform teachers of students' understandings. Although this activity has a science focus, mathematical skills and knowledge are needed to measure, record and process data appropriately. This activity should be carried out in an area that has washable surfaces and a sink for cleaning up spills. The equipment that should be used by each group of students is:
 a rack of 5 test tubes
a rack of 5 test tubes- droppers or pipettes
- universal indicator
- a universal indicator colour chart giving the whole number pH scale 1-14
- HCl (0.1 molL-1) and NaOH (0.1 molL-1) solutions, in beakers or bottles.
If the equipment is available, this could be carried out as a titration, with the acid and base each in a burette. The results will not be linear, rather they will show a titration curve. The universal indicator results should be close to the values expected from calculation (1, 2, 7, 12, 13 respectively).
- Provide students with the acid HCl (0.1 molL-1) and the base NAOH (0.1 molL-1). Support them to form each of the following solutions in a test tube, following the process specified below:
- Place the test tubes with these solutions in the order specified.
- When this process is complete, add one drop of Universal Indicator to each test tube to measure the pH of the solution formed.
- Record all your results in a table.
- Graph the pH of the solution against the proportion of NaOH used to form that solution.
- Support students to make up 5 mL solutions in test tubes, formed in ratio of HCl:NaOH as follows:
- 3:1
- 3:2
- 1:1
- 2:3
- 1:3
As students work, observe their management of ratios (scaling up to form a multiple of 5 parts) and their capacity for finding and expressing a proportion. Use these observations to locate your students on the Patterns and Relationships learning progression. You should also observe the approach students take to recording data in a table, and the appropriateness and accuracy of their graphing.
Discuss, drawing attention to the following points:
- How was the problem of measuring a 5 mL solution based on a ratio of 4 (3:1) or 2 (1:1) parts resolved?
- What was the shape of the graph of proportion of NaOH solution vs pH? (If linear, the students will have ‘curved’ their axes, so this issue will need to be addressed).
- Ask the students: “If we only made three solutions, the 3:2, 1:1, and 2:3, what type of relationship would we think we had”, as an opening to discussion of when we can be certain of a relationship being linear and talk about some non-linear relationships having a linear section.
- Use the fact that pH stands for ‘power of the concentration H+ as a starter for discussion around standard form and the shape of a graph of an exponential relationship.
Session Two
Introducing Ideas
- Together, plan how to make up solutions of NaOH of concentrations of 0.25 molL-1, 0.2 molL-1, and 0.1 molL-1, given a solution of NaOH at 0.5 molL-1, and any amount of distilled water.
Discuss, drawing attention to the following points:
- How do we understand the measurement molL-1 as a concentration?
- How does this compare with gL-1?
- Which measurement would be simpler to use mathematically?
- Why might chemists prefer to use this than gL-1?
Building Ideas
Provide time for students to work through the following questions:
How many mol of NaOH are needed to make a solution, in 1L of distilled water, at a concentration of 0.1 molL-1?
How many mol of NaCl (table salt) are needed to make a solution, in 1L of distilled water, at a concentration of 0.1 molL-1?
- How many mol of HCl are needed to make a solution, in 1L of distilled water, at a concentration of 0.1 molL-1?
Reinforcing Ideas
Provide time for students to work through the following questions:
How many mol of NaCl (table salt) are needed to make a solution, in 0.5L of distilled water, at a concentration of 0.1 molL-1?
How many mol of NaCl (table salt) are needed to make a solution, in 0.5L of distilled water, at a concentration of 0.2 molL-1?
How many mol of NaCl (table salt) are needed to make a solution, in 0.25L of distilled water, at a concentration of 0.1 molL-1?
- How many mol of NaCl (table salt) are needed to make a solution, in 0.25L of distilled water, at a concentration of 0.2 molL-1?
Extending Ideas
Provide time for students to work through the following tasks:
- How many grams of NaCl (table salt) are needed to make a solution, in 1L of distilled water, at a concentration of 0.1 molL-1?
- Convert the concentrations of NaCl at 0.25 molL-1, 0.2 molL-1 and 0.1 molL-1, into gL-1.
- Find a rule to generalise the conversion of any concentration of NaCl given in molL-1 to gL-1. Would this conversion work for any substance, or just NaCl?
Session Three
Introducing Ideas
- Encourage students to set their working out in a table. You might need to model this for some students.
- Pose the following context to students: For a solution of NaOH and HCl to be neutral (pH = 7) there needs to be an equal amount of substance (number of moles) of each.
- How much is NaOH is needed in order to neutralise 1 mL of HCl of concentration 0.1 molL-1 if the concentration of NaOH is 0.1 molL-1?, 0.2 molL-1?, or 0.25 molL-1?
Discuss, drawing attention to the following points:
- Did students solve this problem by considering the concentrations of each reactant? Did they consider what scaling is needed for the NaOH to have the same amount of substance (number of mol) as the HCl?
- How did they students proportional reasoning to solve this problem?
- What were the advantages of setting their working out in a table?
Building Ideas
- Provide time for students to calculate the number of moles of a substance present in:
- 1 L of substance at a concentration of 0.1 molL-1.
- 0.2 L of substance at a concentration of 0.1 molL-1.
- 10 mL of substance at a concentration of 0.1 molL-1.
Reinforcing Ideas
- Provide time for students to calculate the number of moles of a substance present in:
- 2 mL of substance at a concentration of 0.1 molL-1.
- 2 mL of substance at a concentration of 0.2 molL-1.
- 10 mL of substance at a concentration of 0.2 molL-1.
- Provide time for students to calculate the volume of a solution if it has:
- a concentration of 0.1 molL-1 with 1 mol of substance in the solution.
- a concentration of 0.1 molL-1 with 0.1 mol of substance in the solution.
- a concentration of 0.2 molL-1 with 0.1 mol of substance in the solution.
Extending Ideas
- Provide time for students to calculate the number of moles of a substance present in:
- 2 mL of substance at a concentration of 0.1 molL-1.
- 5 mL of substance at a concentration of 0.2 molL-1.
- 10 mL of substance at a concentration of 0.05 molL-1.
- Have students give a general rule for finding the number of moles of a substance present in a given volume of a known concentration.
- Provide time for students to calculate the volume of a solution if it has:
- a concentration of 0.1 molL-1 with 0.1 mol of substance in the solution.
- a concentration of 0.1 molL-1 with 0.2 mol of substance in the solution.
- a concentration of 0.2 molL-1 with 0.25 mol of substance in the solution.
- Have students consider whether they could have used the rule that they found in task 2 to answer task 3?
Session Four
Introducing Ideas
- Provide time for students to look at this graph of volume of HCl added (vertical axis) against volume of 0.1 molL-1 NaOH (horizontal axis) to form a neutral solution (all volumes are in mL).
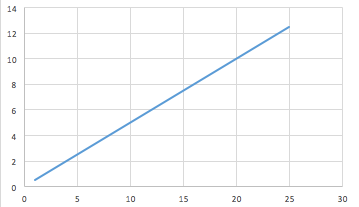
- Have students describe the shape and trend of this graph.
- What is the concentration of the HCl?
Discuss, drawing attention to the following points:
- What is the shape of the relationship shown in the graph?
- What is the gradient of the graph? What is the unit of measure of the gradient?
Building Ideas
Provide time for students to work through the following tasks:
Locate the position on the graph where 10 mL of HCl was added to neutralise the NaOH. We are going to work out the concentration of the HCl from this point.
What is the volume of NaOH that was neutralised by 10 mL of HCl?
The concentration of NaOH is 0.1 molL-1. How many moles of NaOH is present in the volume at that point on the graph?
How many moles of HCl are present at that point on the graph?
How many moles of HCl are present in 10 mL of the HCl solution?
How many moles of HCl are present in 1 L of the HCl solution?
What is the concentration of the HCl solution?
Reinforcing Ideas
- Ask students to consider how the graph would change if:
- the concentration of HCl was doubled?
- the concentration of HCl was halved?
- the concentration of NaOH was doubled?
- the concentration of NaOH was halved?
Extending Ideas
- Provide time for students to give a general rule for the graph of volume HCl vs volume NaOH shown in the starter activity.
- Ask students to consider how the general rule would change if:
- the concentration of HCl was doubled?
- the concentration of HCl was halved?
- the concentration of NaOH was doubled?
- the concentration of NaOH was halved?
Session Five
Introducing Ideas
- Present the following graph to students. This graphs shows the volume of H2SO4 added (vertical axis) against volume of 0.1 molL-1 NaOH (horizontal axis) to form a neutral solution (all volumes are in mL).
Note that there are two H+ ions in H2SO4, but only one OH- ion in NaOH.
H2SO4 neutralises NaOH in approximately the ratio of 1:2 H2SO4:NaOH molecules.
- Encourage the understanding pH as the power of H+ ions.

- Have students describe the shape and trend of this graph. What is the concentration of the H2SO4?
- Discuss, drawing attention to the following points:
- What is the shape of the relationship shown in the graph?
- What is the gradient of the graph?
- What is the unit of measure of the gradient?
Building Ideas
Provide time for students to work through the following tasks:
locate the position on the graph where 10 mL of H2SO4 was added to neutralise the NaOH. We are going to work out the concentration of the H2SO4from this point.
What is the volume of NaOH that was neutralised by 10 mL of H2SO4?
The concentration of NaOH is 0.1 molL-1. How many moles of NaOH is present in the volume at that point on the graph?
How many moles of H2SO4 are present at that point on the graph?
How many moles of H2SO4 are present in 10 mL of the H2SO4 solution?
How many moles of H2SO4 are present in 1 L of the H2SO4 solution?
- What is the concentration of the H2SO4 solution?
Reinforcing Ideas
- Ask students to consider how the graph would change if:
- the concentration of H2SO4 was doubled?
- the concentration of H2SO4 was halved?
- the concentration of NaOH was doubled?
- the concentration of NaOH was halved?
Extending Ideas
- Provide time for students to give a general rule for the graph of volume H2SO4 vs volume NaOH shown in the starter activity.
- Ask students to consider how the general rule would change if:
- the concentration of H2SO4 was doubled?
- the concentration of H2SO4 was halved?
- the concentration of NaOH was doubled?
- the concentration of NaOH was halved?
Session Six
Note that, to simplify idea of neutralisation, only strong acids and strong bases have been used in these examples (e.g. H2SO4 neutralises NaOH in approximately the ratio of 1:2 H2SO4:NaOH molecules).
Introducing Ideas
- Pose the following task to students:
Given 2 mL of each of the following acid solutions;
- 0.1 molL-1 HCl
- 0.2 molL-1 HCl
- 0.1 molL-1 H2SO4
- 0.2 molL-1 H2SO4
What volume of 0.1 molL-1 NaOH would be needed to neutralise the acid?
Discuss, drawing attention to the following points:
How did you solve these problems?
Were you using proportional reasoning?
What pattern or relationship did you notice when solving these problems?
Building Ideas
Provide time for students to work through the following questions:
- What volume of 0.1 molL-1 NaOH would be needed to neutralise 1 mL of 0.1 molL-1 HCl?
- What volume of 0.1 molL-1 NaOH would be needed to neutralise 2 mL of 0.1 molL-1 HCl?
- What volume of 0.2 molL-1 NaOH would be needed to neutralise 1 mL of 0.1 molL-1 HCl?
- What volume of 0.2 molL-1 NaOH would be needed to neutralise 2 mL of 0.1 molL-1 HCl?
Reinforcing ideas
- Pose the following task to students:
Given 5 mL of each of the following acid solutions;
- 0.1 molL-1 HCl
- 0.2 molL-1 HCl
- 0.1 molL-1 H2SO4
- 0.2 molL-1 H2SO4
What volume of 0.2 molL-1 NaOH would be needed to neutralise the acid?
Extending ideas
Pose the following task to students:
- Given 5 mL of each of the following acid solutions;
- 0.2 molL-1 HCl
- 0.05 molL-1 HCl
- 0.25 molL-1 H2SO4
- 0.01 molL-1 H2SO4
What volume of 0.1 molL-1 Ca(OH)2 would be needed to neutralise the acid?
Discuss, drawing attention to the following points:
How would your answers change if Al(OH)3 was used instead of Ca(OH)2?
nb – For the purpose of simplification of the idea of neutralisation, assume that:
HCl neutralises Ca(OH)2 in approximately the ratio of 2:1 HCl:Ca(OH)2, and
HCl neutralises Al(OH)3 in approximately the ratio of 3:1 HCl:Al(OH)3.
Dear parents and whānau,
Recently we have been exploring the mathematics involved in chemical reactions involving acids and bases. Ask your child to share their learning with you.