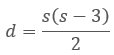The purpose of this activity is to engage students in recognising non-linear patterns, in this case a quadratic relationship. Students might use tables, graphs and equations to represent the relationship between sides of a polygon and the number of diagonals for the polygon.
This activity assumes the students have experience in the following areas:
- Representing linear functions using tables and graphs.
- Working with names and properties of polygons.
- Using finite differences in tables of values to classify linear or non-linear functions.
The problem is sufficiently open ended to allow the students freedom of choice in their approach. It may be scaffolded with guidance that leads to a solution, and/or the students might be given the opportunity to solve the problem independently.
The example responses at the end of the resource give an indication of the kind of response to expect from students who approach the problem in particular ways.
Mathematically speaking, a diagonal of a polygon is a line connecting any two opposite vertices (corners). For example, a pentagon has five diagonals.
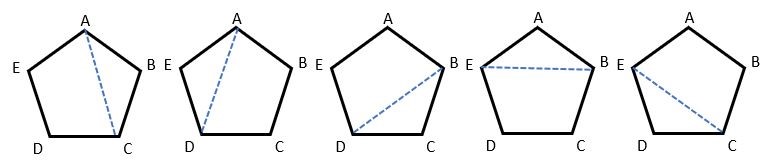
Note that diagonal AC is the same as diagonal CA.
If a pentagon has five diagonals, how many diagonals do polygons with other numbers of sides have?
Is there a pattern for the number of diagonals that allow you to predict the number of diagonals for a hectogon (100 sides)?
The following prompts illustrate how this activity can be structured around the phases of the Mathematics Investigation Cycle.
Make sense
Introduce the problem. Allow students time to read it and discuss in pairs or small groups.
- Do I understand the situation and the words? (Students may need support to understand the meaning of diagonals)
- How do I expect the number of diagonals to increase as I increase the number of sides?
- Does this look/sound like a problem I have worked on before?
- Do I expect there to be a pattern?
- What will my solution look like? (The solution will be general rule the gives the number of diagonals derived from the value of n. The rule might be expressed as an equation.)
Plan approach
Discuss ideas about how to solve the problem. Emphasise that, in the planning phase, you want students to say how they would solve the problem, not to actually solve it.
- What strategies will be useful to solve a problem like this? (A table or graph will be helpful in organising the data. Drawing diagrams of diagonals for given polygons will be helpful?
- Which polygons would be the easiest ones to start with?
- How will I look for a relationship between the number of sides and number of diagonals of polygons?
- What tools (digital or physical) could help my investigation?
Take action
Allow students time to work through their strategy and find a solution to the problem.
- Have I shown my workings in a step-by-step way?
- Is my recording systematically organised?
- Have I looked for efficient ways to find the number of diagonals, possibly without drawing?
- Have I identified any relationships?
- How can I express the relationships I found using words and symbols?
- Does my rule work for polygons that I haven’t checked?
- How do my results look different or different to others? Why could this be?
- Do others have better ways to solve the problem?
Convince yourself and others
Allow students time to check their answers and then either have them pair share with other groups or ask for volunteers to share their solution with the class.
- Is my working clear for someone else to follow?
- Did I try enough cases (polygons) to be confident in my rule?
- How would I convince someone else I am correct?
- Is my rule expressed in a mathematical way? Can my rule be reversed to find the number of sides for a given number of diagonals?
- Would my strategy work in a different situation?
- Is there some mathematics I need to learn to solve similar problems?
- What have I noticed that seems to work all the time in these types of problem?
- Do I have words and symbols to name the type of function I found?
Examples of work
Work sample 1
The student uses patterns in the numbers within a table to find a general rule.
In this approach students are likely to privilege arithmetic reasoning by creating a table of values for polygons of different numbers of sides.
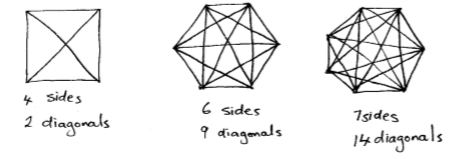
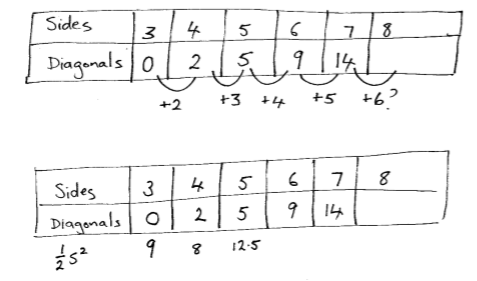
They may then calculate differences between terms and note a pattern in the growth of those differences. Noting the differences will allow students to predict the number of diagonals for other polygons with more sides.
Experience with simple quadratic patterns may help students see that the second order difference of one is half that which occurs with square numbers. They may try investigating halves of squares to find the relation though this approach is complex.
You might suggest doubling the number of diagonals to look for a pattern since each diagonal connects two corners, e.g. AC is the same as CA. That allows for opposite directions and makes pattern spotting much easier. Looking for factors that produce double the number of diagonals is a fruitful approach.
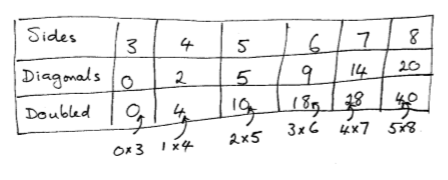
Students may spot that the factors of double the diagonal totals are always three less than the side number multiplied by itself. If that product is halved it gives the general rule for diagonals. Let d represent the number of diagonals and s represent the number of sides.
Work sample 2
The student uses the spatial situation to generalise the number of diagonals emanating from each vertex and extend that idea to generalise the total number of vertices.
A figural (spatial) approach is potentially very fruitful for this task. Starting with the simple case of the pentagon students might notice that from each vertex two diagonals can be drawn.
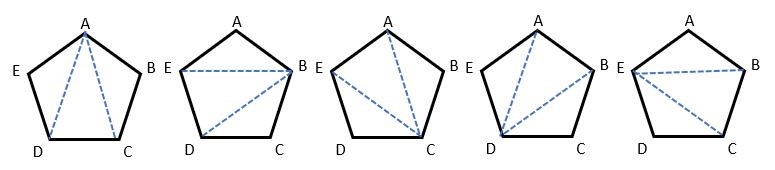
That makes a total of 5 x 2 = 10 diagonals but that includes double ups. Since each diagonal is drawn twice dividing by two gives the actual number. In general for any n-gon, n-3 diagonals can be drawn from each vertex since diagonals cannot be drawn to the vertex itself or to its two adjacent vertices. Therefore, for any n-gon, the number of diagonal from each vertex is n(n-3). Since the diagonals will be double counted the product must be divided by two. That yields the general formula: