New Zealand Curriculum: Level 2
Learning Progression Frameworks: Measurement Sense, Signpost 2 to Signpost 4
Target students
These activities are intended for students who can compare the lengths of objects by direct comparison, that is, by bringing the objects together. They may be able to use an informal unit of length such as a counter or cube, and count all the units to establish a measure, making statements such as “my book is 12 cubes long.”
Students should be able to count on or back, or use early part-whole thinking to find the total of two sets (addition) or the result of removing objects from a set (subtraction).
The following diagnostic questions indicate students’ understanding of, and ability to compare the areas of flat spaces, particularly rectangles. Allow access to pencil and paper and to a calculator if needed. (show diagnostic questions)
The questions should be presented orally and in a written form so that the student can refer to them. The questions have been posed using a pancake and waffle context but can be changed to other contexts that are engaging and culturally relevant to your students.
- Here are two pancakes.
Which pancake is the biggest?
Which pancake would take the most bites to eat?
(Use page 2 of the Copymaster to print, laminate and cut out the pancakes. Use A and B.)
Signs of fluency and understanding:
Uses visual comparison or overlaps the pancakes physically to establish that A has more area than B.
What to notice if they don’t solve the problem fluently:
Attends to length, rather than area and chooses B over A. This may indicate that the student needs experience with differentiating area from length.
Supporting activity:
Comparing areas
- Here are three more pancakes
Please put the pancakes in order from smallest to biggest.
(Add pancakes C, D, E to A and B from above).
Signs of fluency and understanding:
Orders the five pancakes by visually comparing or overlaying one pancake on top of the other. Tests pancakes for area two at a time and controls the order relationships. Clearly shows A has greater area than B and E and that C is smallest. May consider that B and D are approximately equal so any order of these three pancakes is accepted.
What to notice if they don’t solve the problem fluently:
Attends to length rather than area and chooses B is greater than A. This indicates the student needs experience with differentiating area from length.
Unable to see that B and D are approximately the same area by imaging shifting parts of the areas to create a matching shape. This may indicate that the student needs experiences with altering shape while conserving area.
Has difficulty organising the five pancakes in order using pair comparison. This may indicate that the student needs support in seriating more than two objects.
Supporting activity:
Ordering areas
- Each pancake has one bite taken out of it. The bites are the same size.
Which pancake takes the most bites to eat?

Allow the student to draw ‘bites’ on the pancakes if necessary.
Signs of fluency and understanding:
Consistently 'eats' each pancake with bites of the same size. Covers each whole pancake with no obvious gaps or overlaps. Counts the bites to decide which pancake takes the most bites.
What to notice if they don’t solve the problem fluently:
May not maintain a consistent bite size.
May not cover each pancake without gaps or overlaps.
Both behaviours indicate that the student needs more experience using a self-chosen unit to compare areas of object.
Supporting activity:
Using an informal unit for area
- Which waffle is the biggest, the circle or the square?
Explain how you know using the markings.

Signs of fluency and understanding:
Counts the number of squares in each waffle, allowing for complete and partial units. Concludes that the square is larger because it has 16 complete squares. The circle also has 16 squares but some of those squares are incomplete.
May argue that the square and circle are equal in area because the curved parts of the circle might ‘fill in’ the partial squares.
The key idea is that the square units are counted in some way. Most students will use counting or repeated addition though advanced students may use multiplication, i.e., 4 x 4 = 16.
What to notice if they don’t solve the problem fluently:
Unable to use the squares to make a judgment about comparative area of the shapes. This may indicate that the student needs experience in filling flat spaces with identical units.
May confuse the two attributes, area, and perimeter, when providing answers. For example, “The circle is bigger because it is further around.” This may indicate that the student needs support distinguishing the two attributes, perimeter is a length and area is flat space.
May have difficulty using partial units and either ignore them or be unsure of how to allow for half units in determining area. This may indicate that the student needs experience in finding areas of shapes that include partial units.
Supporting activity:
Using units and partial units to measure area
- What is the area of each waffle in square centimetres?
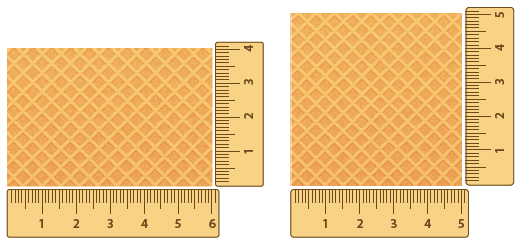
Make a calculator available if the student needs it.
Signs of fluency and understanding:
Measure the side lengths using the rulers provided in the picture.
Correctly image the array of square centimetres and calculate the area. Use repeated addition or multiplication to find the area; 6 x 4 = 24 cm2 and 5 x 5 = 25 cm2.
What to notice if they don’t solve the problem fluently:
May be unsure about how to find area in square centimetres, although they may still measure the side lengths correctly. This may indicate that the student needs opportunities to fill spaces with arrays of squares and to use multiplication to find areas.
Supporting activity:
Measuring areas using square centimetres
Teaching activities


