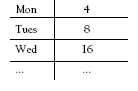See the notes for Bean Counters (page 21) on the reasons for students having and using a broad range of multiplicative strategies.
For this activity, students need to be already familiar with the following multiplicative strategies:
• Place value partitioning: partitioning a number (using place value), multiplying the parts separately, and then adding the products.
5 x 48 = (5 x 40) + (5 x 8)
= 200 + 40
= 240
(see Sticking Together, pages 10–11)
• Using tidy numbers and compensating: working out 5 x 50 instead of 5 x 48 because 50 is a tidy number and easy to multiply. But then we have to compensate because we have got 5 groups of 2 more than we need, so we subtract them again.
5 x 48 = (5 x 50) – (5 x 2)
= 250 – 10
= 240
(see Bean Counters, pages 8–9)
• Doubling and halving (making proportional adjustments): doubling one factor and halving the other gives you the same answer and may make the calculation easier.
5 x 48 = 10 x 24
= 240
(see Face the Facts in Multiplicative Thinking, Figure It Out, Levels 2–3, page 6).

This activity is suited to a guided teaching session with a group because there are lots of opportunities for discussion. Introduce the activity by getting your students to solve Mr Mannering’s problem before they look at how the students in the book solve it. Discuss the different strategies your group used and use this discussion as an opportunity to remind the students of the meaning of the terms “place value”, “tidy numbers”, and “doubling and halving”.
The aim of this activity is to help the students learn to make wise decisions about which strategy to use in a particular situation. In order to do this, they need to be able to look at a problem before they solve it and identify features that would prompt them to use one strategy rather than another.
Promote generalisations by asking questions such as:

• Look at the problem before you start working it out; which strategy do you think would be most efficient here?

• What is it about this problem that makes you want to use that strategy?

• List all the problems in the activity and group them according to the strategy you thought was most efficient for each problem. (It may be valid to have some problems in two groups if both strategies are equally efficient for those problems.)

• What do all the problems in each group have in common?

Useful responses will include these ideas:

Doubling and halving: This strategy is useful if it can change the calculation into a known fact or one that is easy to work out, such as 10 times. At least one of the factors should be even so that halving it gives us a whole number.
Tidy numbers and compensating: One of the factors has to be close to a tidy number so there isn’t too much compensating to do.
Place value partitioning: This strategy suits a wide range of problems, but it can be difficult to keep track of if there’s a lot of renaming to do when you’re adding up the parts. It’s easier to use if the digits are small.

Extension

Students could create a flow diagram that shows what they would look for when confronted with a problem and how their strategy decision-making process might progress. They could start by asking “Is the answer to this problem a known fact?” and then ask questions such as “Is the problem 5 times or 50 times something?” If the answer is yes, “Use doubling and halving to create a 10 times or 100 times problem and solve it”; if the answer is no, “Would doubling and halving the problem turn it into a known fact?” and so on.
 

Answers to Activities

1. a. i. Manua
ii. Sophie
iii. Larry
b. Answers may vary. Manua’s method involved the simplest calculations and was very efficient in this case.
2. a. i. (5 x 100) – (5 x 2) = 500 – 10 = 490
ii. (5 x 90) + (5 x 8) = 450 + 40 = 490
iii. 5 x 98 = 10 x 49 = 490
b. Answers may vary. Sophie’s method involved the simplest calculations and was very efficient.
3. a. Discussion and choice of methods will vary.
i. This would be a good problem for using doubling and halving, because doubling
5 times makes it into 10 times, which is easy to calculate, and the other factor
is an even number, which is easy to divide. The other two methods would
also work well but involve slightly more calculations (using tidy numbers and
place value).
ii. This would be a good problem for using place value to break up the 43. Using
tidy numbers is also possible, but 43 is not very close to a tidy number so the
calculation is a little harder. Doubling and halving is not useful in this case:
both numbers are odd, so it doesn’t help to halve one of them.
iii. This would be a good problem for using tidy numbers because the 79 is very
close to a tidy number. Doubling and halving won’t help. 79 could be broken
up using place value, but the calculations will be more difficult than calculations
using a tidy number.
b. Discussion about the most efficient method will vary. Possible working for each problem is:
i. Tidy numbers
5 x 26 = 
5 x 26 = (5 x 30) – (5 x 4)
= 150 – 20
= 130
Place value
5 x 26 = (5 x 20) + (5 x 6)
= 100 + 30
= 130
Doubling and halving
5 x 26 = 10 x 13
= 130
ii. Tidy numbers
43 x 7 = 
43 x 7 = (50 x 7) – (7 x 7)
= 350 – 49
= 301
Place value
43 x 7 = (40 x 7) + (3 x 7)
= 280 + 21
= 301
Doubling and halving
43 x 7 = 86 x 3.5 = 301 or 21.5 x 14 = 301 so 43 x 7 = 301. (In both cases, this
strategy makes the calculation harder, not easier.)
iii. Tidy numbers
6 x 79 = 
6 x 79 = (6 x 80) – (6 x 1)
= 480 – 6
= 474
Place value
6 x 79 = (6 x 70) + (6 x 9)
= 420 + 54
= 474
Doubling and halving
6 x 79 = 12 x 39.5
= 474
(This strategy makes the calculation harder, not easier.)
4. a. Problems will vary.
i. The problem should have one number that is close to a tidy number to make
it easy to solve.
ii. This strategy suits many problems, but it’s the easiest to use if one number in the
problem is a single-digit number and there isn’t much renaming involved.
iii. This strategy suits 5 times or 50 times problems because these numbers double
to make 10 times or 100 times, which are easy to calculate with. Other problems suit
this strategy if they can be changed into known facts, for example:
4 x 16 = 8 x 8 = 64.
b. Practical activity. See points in 4a.

Game

This activity is based on an ancient Chinese game in which players had to make given totals by using four single-digit numbers and the four operations. Thirty-one is a good target as there are many ways in which students can reach this score. Students could use a tally sheet to record who has the highest score in each round.
After students have played the game several times, the target number can be changed. Students may wish to describe why it is easier to get a target of 31 than a target of 13. Similarly, they can be given a target total such as 27 and asked to write as many four-digit combinations for it as they can.
For example:

Where students use different types of calculators, particularly scientific and four-function, the issue of order for operations may arise. For example, given 4 + 6 x 3 – 5 = , a scientific calculator will get 17 whereas a four-function calculator will get 25. Four-function calculators perform calculations in the order of keying, that is, 4 + 6 = 10, then 10 x 3 = 30, and then 30 – 5 = 25.
A scientific calculator uses the convention for operations, that is, multiplication and division are calculated before addition and subtraction. With 4 + 6 x 3 – 5 = , the 6 x 3 = 18 is performed first, and then 4 is added and 5 subtracted: 18 + 4 – 5 = 17.

Activity

Students will need to approach this systematically. A table would be useful.

Answers to Activity

Game

Game of addition, subtraction, multiplication, and division
Activity

64 plums

The following prompts illustrate how this activity can be structured around the phases of the Mathematics Investigation Cycle.

Make sense

Introduce the problem. Allow students time to read it and discuss in pairs or small groups.

• Do I understand the situation and the words? (Students may not be familiar with saving in a piggy bank.)
• What are the important words and symbols? (Knowing that 1 year has 12 months is important.)
• What will my solution look like? (The solution will give the total amount saved by Bill, supported by calculations.)

Plan approach

Discuss ideas about how to solve the problem. Emphasise that, in the planning phase, you want students to say how they would solve the problem, not to actually solve it.

• What are the maths skills I need to work this out? (Students should recognise the need to understand years and months, and that multiplication will be applied.)
• How could I show this problem using numbers, pictures, graphs, tables, or materials?
• What could the solution be? What is a sensible estimate?
• What tools (digital or physical) could help my investigation?

Take action

Allow students time to work through their strategy and find a solution to the problem.

• Is my strategy working? Is there a more efficient way to solve the problem? (Note the preferencing of multiplication instead of repeated addition.)
• Have I recorded my ideas in a way that helps me to see patterns? (Sequences of equations that are systematic will reveal patterns involving multiplication.)
• Are there any patterns?
• How might I describe the pattern? 
• Does my answer seem correct? Is it close to my estimation?
• How could I make sure that I haven’t missed anything?
• Does my solution answer the question?
• Is there another possible way to solve it?

Convince yourself and others

Allow students time to check their answers and then either have them pair share with other groups or ask for volunteers to share their solution with the class.

• What is the solution? It my solution clear?
• Is my working clear for someone else to follow?
• How would I convince someone else I am correct? Have I justified what I did?
• Could I have solved the problem in a more efficient way?
• Is my strategy suitable for other problems? What kinds of problems is it suitable for?
• What maths have I used to solve the problem, including knowledge and strategy?

Examples of work

Work sample 1

The student combines additive and multiplicative thinking to solve the problem.

Click on the image to enlarge it. Click again to close. 

Work sample 2

The student applies the distributive property of whole numbers under multiplication to solve the problem. They round the multiplier and adjust the product correctly.

Click on the image to enlarge it. Click again to close. 

Session 1

1. Begin with a growth problem (see PowerPoint 1: Eggs and chickens).
   There are 12 eggs in one dozen.
   How many eggs are in eight dozen?
   What ways can you find to solve this problem?
   Which way is the most efficient? (takes the least effort)
    
2. Let your students work in small groups to answer the question. Provide place value materials such as connecting cubes, place value blocks, or iceblock sticks and rubber bands for students to access if they wish. Real empty egg cartons are very handy for later.  Encourage students to rehearse the strategy they used so they are ready to share it with the whole class. After an appropriate time, bring the class together for discussion. Have eight egg cartons with cubes or counters as ‘make-believe’ eggs available to show what happens to the quantities.
   
   Some students may use additive thinking. An example might be:
   12 + 12 = 24 (That’s two cartons), 24 + 24 = 48 (That’s four cartons), 48 + 48 = 96 (Possibly using 50 + 50 = 100, that’s eight cartons).
   
   You might record the strategy using multiplication, like this:
   2 x 12 = 24 → 4 x 12 = 48 → 8 x 12 = 96
   
   Repeated doubling can be a useful strategy for multiplying by 4, 8, and 16.
   
   Additive thinking gets the job done but it is an inefficient process. Look for multiplicative strategies to highlight and share. These strategies might include:
   12 is made up of ten and two. 8 x 10 = 80 (That’s the tens) and 8 x 2 = 16 (That’s the twos). 80 + 16 = 96.
   
   Or (less likely):
   10 x 12 = 120 (That’s two dozen too much) 2 x 12 = 24 (That’s two dozen)
   120 – 24 = 96
   
   Both strategies use the distributive property which means one factor is ‘distributed’. In this case 12 is distributed into 10 and 2, and 10 is distributed into 8 and 2.
    
3. Use the egg carton model to show how each strategy works, including the repeated doubling. PowerPoint 1 can be used if you do not have the physical model of egg cartons. Pose this problem for the students to solve in small groups of two or three (See PowerPoint One). Let students have access to materials if they need them.
   There are 15 rashers of bacon in each pack.
   How many rashers are in six packs?
   What different ways can you find to solve this?
    
4. Look for students to:
   • Apply multiplicative strategies rather than additive ones.
   • Recognise which strategies are the most efficient.
   • Record their strategies using equations or other written working.
   • Show how their written recording can be represented with physical materials.
      
5. After a suitable time, bring the class together to share ideas. Look for students to think critically about how a multiplier of 6, rather than 8, changes their use of strategies. Six does not lend itself to doubling only strategies though doubling then multiplying by three, or vice versa, works.
   
   Good examples of using the distributive property are:
   15 = 10 + 5, 6 x 10 = 60 and 6 x 5 = 30. Therefore, 6 x 15 = 60 + 30 = 90.
   6 = 5 + 1, 5 x 15 = 50 + 25 = 75 and 1 x 15 =15. Therefore, 6 x 15 = 75 + 15 = 90.
   
   An example of using the associative property is:
   6 = 2 x 3, 2 x 15 = 30, 3 x 30 = 90. Therefore, 6 x 15 = 90.
    
6. Ask students to show what each strategy looks like with materials. Place value-based models are particularly good for this problem. If time permits take each problem (Eggs and Bacon) and change the numbers. For example, you might create a tray of 24 eggs. How many eggs are in three trays?

Session Two

1. Remind your students of problems they solved the session before. You might show them some examples as a reminder.
   What was the same about these problems? What was different?
    
2. Students should note that while the stories and numbers were different there was a common structure to the problems they solved. That structure involved a collection or set of some kind, like a packet, and a multiplier that gave how many of the collections were considered. Take one problem and ask your students:
   Where is the collection or set in this problem?
   Where is the multiplier?
    
3. Provide a different problem and ask the same questions. You might use:
   Eighteen hens lay four eggs each in one week.
   How many eggs is that in total?
   
   Be aware that students might think that the multiplier is always less than the size of the equal collections. Share some strategies for solving 18 x 4 = 72.
    
4. Pose this challenge which involves computational thinking.
   Imagine you trained a robot to solve problems like these ones. Make up a set of instructions for the robot. What actions should the robot take? Put the actions in order.
    
5. Let your students work in small teams to devise a set of instructions. Look for them to:
   • Define the equal collections and multiplier as factors, with some criteria
   • Record the factors and steps symbolically
   • Follow a sequence of instructions that work to give the correct product
      
6. The aim of the follow-up discussion is to create an algorithm, a set of steps that will reliably produce the answer. Act out some instructions that students provide with the example problem. Have place value materials available to check what is going on with quantities as the steps are followed.
   
   You might end up with a sequence that looks like this:
   Step 1: Find the number of things in the equal collections, call that number [c]
   Step 2: Find the number of equal collections, call that number [n]
   Step 3: Multiply [n] and [c] by:
   • Breaking up [c] into the number of tens [a] and ones [b]
   • Multiplying both [a] and [b] by n
   • Add the two answers, n x a and n x b, together
      
7. Challenge your students to adapt their algorithm to solve this problem in small groups (see Copymaster 3):
   There are 144 eggs on each pallet.
   You have 4 pallets. How many eggs is that altogether?
    
8. Provide place value materials to support students to work out the product. Look for students to:
   • correctly establish 144 as the multiplicand - the size of the equal collections
   • correctly identify 4 as the multiplier
   • recognise that 144 contains hundreds as well as tens and ones
   • multiply hundreds, tens and ones separately then add the partial products.
      
9. Ask how the set of procedures needs to be changed to accommodate the new problem. Do students recognise the two steps that need minor change?
   
   Be open to other ways that students might solve 4 x 144, particularly repeated doubling, i.e. 2 x 144 = 288, 2 x 288 = 576. You might try writing an algorithm for the doubling strategy. That will require a first step of deciding whether, or not, the numbers are suitable.
    
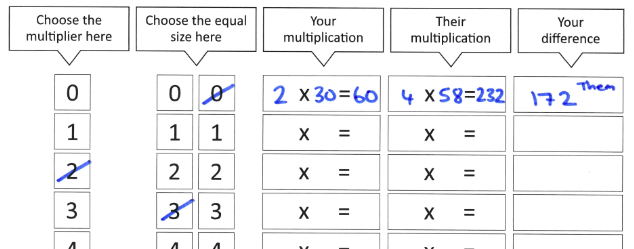
10. Finish the session with Copymaster 1 that is a paper game for practising multiplication of a two-digit number by a single digit number. Some students may need a calculator to support their participation.
    
    The rules are:
    Players play in pairs. Each person has their own sheet of paper (Copymaster 1)
    1. At the same time they choose two factors by crossing off digits. The first factor is single digit and the second factor has two digits. Players do no know what digits their opponent is choosing.
    2. Players multiply their factors and record the product on the game sheet.
    3. Both players compare their products. The player with the largest product wins the round. They get the difference between their product and their opponent’s product.
    4. The player with the highest total of differences wins.
       
       Here is an example of a partly completed scoresheet.
       

Session Three

In this session students transfer the strategies they developed for multiplication to problems involving division. Understanding that asking themselves the question, “How many x’s fit in y?” structures division problems and supports students’ fluency in calculation. By connecting division to multiplication students learn to apply their multiplication strategies and connect multiplication and division as inverse operations.

1. Begin with this division problem:
   Henrietta gathers 52 eggs one morning.
   How many half-dozen cartons (six-packs) can she fill?
    
2. You may need to clarify with the students that a half-dozen carton holds six eggs. Let the students explore the problem in small teams, using materials for support, if needed. Ask your students to record their strategies to share with the class. Do your students…?
   • Use additive thinking to ‘build up’ to a solution, e.g. 6 + 6 = 12, 12 + 12 = 24, 24 + 24 = 48, leaves 4 eggs to make 52.
   • Use multiplicative ‘build up’ strategies, e.g. 5 x 6 = 30 so 6 x 6 = 36 … 8 x 6 = 48.
   • Use the distributive property of multiplication, e.g. 10 x 6 = 60 (too many eggs) so 9 x 6 = 54 and 8 x 6 = 48, therefore 8 six-packs are possible with 4 eggs remaining.
   • Apply basic facts knowledge, e.g. 8 x 6 = 48 and 9 x 6 = 54 and 52 lies between the two products.
   • Pay attention to how students handle the remainder of 4 eggs. 
     How much of a six-pack are four eggs? (two-thirds)
      
3. Gather the class to share strategies. Choose teams that use strategies representative of the points above. Discuss efficiency. Which strategies require the least work?
    
4. Introduce division equations in the context of the eggs problem.
   52 ÷ 6 = 8 r4
    
5. Make the meaning of the symbols explicit , i.e., equals as a sign of balance, division as meaning “measured in units of”, 52 as the dividend (total items to be measured), 6 (unit of measure), 8 (number of equal units that fitted), and r4 as the ‘leftovers’ or remainder. You might discuss other ways that the remainder might be recorded, i.e. ⁴/₆ of a carton, 0.66… of a carton.
    
6. Pose the following ‘bits missing’ problem. Let the students make up the missing data in the problem, i.e., number of eggs collected, and size of the carton.
   Henrietta gathers __ eggs one morning.
   How many __ cartons can she fill?
    
7. Encourage the students to solve more than one problem with a focus on this question:
   How do your strategies change as the numbers in the problem change?
   
   Observe how students approach the task. Challenge students who ‘play safe’ to try more difficult numbers.
   What numbers do you think would make the problem more challenging?
   Why do the problems become more difficult with those numbers?
   What strategies do you use with more challenging problems?
    
8. After a suitable time gather the class together to process their problems. Categorise the problems as easy, medium and hard.
   What makes a problem easy? (small numbers, no remainder, access to basic facts)
   What makes a problem hard? (bigger numbers, remainders, tricky divisors such as three or seven, or outside the range of basic facts)
    
9. Choose one hard problem and ask the students to solve it. Discuss what knowledge might be handy for solving it?
   How will we use that knowledge?
    
10. Make a list of strategies such as distributing the dividend, rounding up to a tidy number, halving, etc.

Session Four

1. Recap the previous session using examples of the problems that students created. Record the problems using division equations, e.g. 72 ÷ 4 = 18. Ask students to be explicit about what the symbols represent in the equation.
   What is the same about these problems? (all the problems are about measurement, i.e. How many x’s fit into y?)
    
2. Tell the students that they will solve a different type of division. Pose this problem:
   Three hens laid 48 eggs altogether over two weeks.
   Each hen laid the same number of eggs.
   How many eggs did each hen lay?
    
3. Let students solve the problem in small teams. Allow them to use materials if needed. Encourage students to record their strategies for sharing later. Look for students to:
   • Recognise that the problem involves sharing the eggs into three equal sets.
     Note that the problem semantics suggest multiplication, i.e. 3 x □ = 48.
   • Use efficient build up strategies that involve multiplication, e.g. 3 x 10 = 30 (18 eggs left), 3 x 5 = 15 (3 eggs left), 3 x 1 = 3, so each hen lays 10 + 5 + 1 = 16 eggs.
   • Possibly use place value with tidy numbers, e.g. 60 eggs would mean 20 eggs each, 48 is 12 eggs less so each hen gets 4 eggs less than 20.
      
4. Gather the class to share strategies. Look for a team of students that work the problem out as “How many threes are in 48?” If no students do that then introduce the idea as your strategy.
   Can someone explain how that works? The problem is about sharing not measuring.
    
5. You may need to act the problem out with materials, like cubes, to support students see the connection between the two forms of division. Deal out ‘eggs’ to three students acting as ‘hens’, pausing each time around is complete.
   How many eggs have I shared so far?
   
   Students should notice that three eggs are used up each time a round of dealing is complete.
   Why are three eggs used up each time?
    
6. Provide your students with Copymaster 2 which contains variations on the first problem. They can solve the problems individually or in small teams. Encourage them to use their multiplication facts and ask, “How many x’s are in y?” thinking.

Session Five

In this session students explore an open-ended problem that allows them to demonstrate their multiplication and division strategies. The problem requires them to impose or find some information, i.e., the number of hens, how many eggs hens lay per week, and the size of the trays. Invite them to research online if they need to and use their knowledge of everyday context, e.g., trays that eggs commonly come in.

1. Use Copymaster 4 to introduce the problem and allow students to work on the task independently. Insist that they show their working clearly so someone else can see their reasoning.
   On Happy Chook poultry farm there are about 80 free range hens.
   Each Saturday all the eggs for the week are sold at the Farmers’ Market.
   How many trays are needed each week?
    
2. After a suitable time put the students in pairs to compare their work. Ask some reflection questions such as:
   Was there enough information to solve the problem?
   If not, where did you get your information?
   Were your strategies efficient?
   How might you have solved your problem differently?
    
3. Gather the work samples as evidence of your students’ current thinking about multiplication and division.