Getting Started

In this session we use loops of string or elastic to form shapes according to given requirements. We then convince others that our shape meets the requirements.

1. Put students into groups of 4. Consider organising these groups to contain students of mixed abilities and mathematial confidence levels. Give each group a length of string or elastic - approximately 2 to 3 metres long. Have them tie the ends of the string in order to make a loop.
2. Pose the following task:
   Use the members of your group and the loop of string to make a shape that has four equal sides.
3. Allow the students to experiment. Provide questions that focus on the symmetry of the shape and the ‘squareness’ of the corners. For example:
   How did you find each of the equal length sides?
   Using the string, how might you show any lines of reflective (line) symmetry?
   How might you show whether the corners are right angles (without using a protractor)?
   Convince another team member that your shape is correct.
4. Let students share their shapes before gathering the class.
   What is the mathematical name for your shape? 
   Most groups will create squares, but some groups may create rhombi (rhombuses).
   What properties must a shape have to be a square? (Four equal sides, four right angles, two pairs of parallel sides)
   Are there other shapes that have four equal sides? 
   What are those shapes called? (Rhombi)
   What are the properties of a rhombus? (“Four equal sides” is the only defining property. Note: Opposite angles are equal so there are two pairs of equal angles.)
   Is a square a kind of rhombus? (Yes. It has four equal sides).
5. You might draw a large Venn Diagram on the floor or whiteboard to illustrate the set and subset relationship of rhombi and squares. Ask students to draw squares and rhombi to add to the diagram. This could also be done on a PowerPoint - and students could complete the Venn Diagram in pairs. Make sure that they realise that the squares, inside the smaller circle, are also counted as rhombi, since they are also inside the larger circle.
   
   Turn various shapes so they appear differently, and ask:
   Is this still a square/rhombus? Why? (Orientation does not effect the properties of the shape.)
6. Now challenge the groups to use the loop of string to complete this task:
   Use the members of your group and the loop of string to make a shape that has four sides, two of which are parallel.
   You may need to define parallel first before groups start work. Look up a definition online. Railway tracks are a good metaphor.
7. After a suitable time, groups can share their shapes and justify that the shape they created meets the criteria. Most groups are likely to make parallelograms or rectangles, but some may form trapezia. Each class of shape is correct.
8. Define each class of shapes, first by asking students about the properties they see, then providing them with a definition.
   • Parallelogram: Quadrilateral with opposite sides that are parallel
   • Rectangle: Quadrilateral with four right angles
   • Trapezium: Quadrilateral with only one pair of opposite sides that are parallel.
     Note: In the US, a trapezium refers to a quadrilateral with no parallel sides, and some definitions of trapezium refer to at least one pair of parallel sides, therefore including parallelograms.
9. Is a rectangle a special parallelogram?  (Yes, all rectangles have two pairs of parallel sides, so they are all types of parallelograms).
   Is a trapezium also a type of parallelogram? (A trapezium has only one pair of parallel sides, so it is not a parallelogram).
10. Use your loop of string to make the following triangles:
    • a triangle that has no sides that are the same (scalene)
    • a triangle that has only 2 sides the same (isosceles)
    • an equilateral triangle.
11. After making each type of triangle, the group must prove that the necessary conditions are met. Though the conditions involve side length it is important to focus attention on angles. Use 90⁰ (a right angle) as a benchmark. Most triangles that students create have angles less than 90⁰.
12. Can you form a triangle with an angle greater than ninety degrees? Try. (Yes, e.g. 120⁰, 35⁰, 25⁰)
    What is true about the interior angles of an equilateral triangle? (Equal angles)
    Can a triangle have one right angle? (Yes) Make a triangle like that.
    Can a triangle have two right angles? (No)
13. Ask the students to create a set of criteria for their own shape. The shape can have up to eight sides and there can be up to four criteria. Each group needs to provide a model answer to their teacher, with awareness that more than one class of shape might be possible.
14. Gather as a class. Ask groups to provide their criteria while the other groups construct the shape with string or elastic. Shapes could be compared and further explored with the use of a digital tool. Search for “shape manipulatives online” to find an appropriate site.

Session 2

Over the next few sessions, students create Te Whānau Taparau (The Polygon Family) by transforming a circle. You could introduce the key ideas in this session using the book The Greedy Triangle, by Marilyn Burns. This session introduces a significant amount of te reo māori vocabulary. Always accompany these terms by their English translations and pictures/materials to support students’ understanding of the new terms.

The Circle

1. This is a story about a shape from the porowhita (circle) whānau who wanted to be part of the taparau (polygon) whānau. He was a special porowhita because he was able to transform himself into other shapes by folding and unfolding. However, he needed the help of a mathematician who knew some things about geometry ... that person is you!
2. Either give the students a set of porowhita, or give the students a piece of A4 paper and ask them to make the largest possible circle using drawing compasses. Discuss how the students worked out the biggest circle. If compasses are not available simply trace around a circular plate or lid.
3. Discuss the attributes of a circle.
   What makes a circle different from polygonal shapes, for example the triangle (tapatoru), square (tapawhā) or the parallelogram (whakarara)?
4. Students should note that polygons have straight sides. In fact, a polygon is a 2-dimensional shape that is bounded by three or more straight sides.
5. Is a circle a type of polygon? (No. A circle is bounded by a curved ‘side’.)
   What are some names that are used to describe parts of a circle?
6. Focus the students on:
   • diameter (rangiwhitu), radius (putoro) and circumference (pae)
   • the relationship between te rangiwhitu and te putoro. The radius equals half the diameter.
7. It is important for students to consider the idea of a circle as a locus, an infinite set of points that meet a condition or set of conditions. Take your students outside with skipping ropes and chalk. Challenge them in teams of three or four.
   Use your rope and chalk to create a perfect circle.
8. Students are likely to try many different techniques, but the most successful method is to emulate a "tethered pony". One student fixes an end of the rope to spot (the centre), while another walks around them with the rope kept taut. That student traces their path with chalk.
9. The defining property of a circle is that it is a set of points the same distance from the centre. The length of the rope is the radius of the circle.
   The relationship between pae and rangiwhitu is an extension or extra investigation, usually reserved for later levels. Pi (3.14…) is the ratio of circumference to diameter, that is the circumference equals the diameter multiplied by pi.
10. Return to the class and challenge your students to:
    Find the centre of your paper circle. What methods can you find?
11. Folding the circle in half in two different orientations creates an intersection of diameters. The point of intersection is the centre.

The circle becomes an equilateral triangle

1. We now continue the activity to transform the circle:

   Porowhita looked in the mirror one day and decided he was getting bored of being a circle. Porowhita decided that he wanted to look just like tapatoru rite. He needs your help.
   Using the circles (provided or made), fold Porowhita to make the biggest possible tapatoru rite (equilateral triangle). You may need to experiment with different ways of folding to get the largest one possible.

2. Develop a method that you will use in order to check that the shape you have made satisfies the requirements needed for a tapatoru rite (equilateral triangle), and that it is the largest equilateral triangle possible.
3. If this task is too challenging for the students, you may need to give a hint (refer to the diagram) or show one that has already been made, to convince students that it can be done.
    

4. Focus the follow-up discussion on the rotational and reflective symmetry of the triangle.
   How many lines of reflective symmetry does the triangle have?
   Where are the lines located?

   Does the triangle have rotational (turn) symmetry?
   Why must the internal angles be equal for the shape to have rotational symmetry?

5. What other types of triangle can be folded from a circle?
   What happens if you do not fold into the centre of the circle?
   Is a right-angled triangle possible? (One side to the triangle must be the diameter)
6. It would be worthwhile getting the students to develop methods to check for other tapatoru rite (equilateral triangle), and in so doing, develop the relationship between length of the sides and size of the angles.

Session 3

Triangle to trapezium

1. So, Porowhita (circle) not only changes his shape, but also changes his name to Tapatoru rite (equilateral triangle). At the end of the week Tapatoru rite feels cramped - he can't roll around like he used to when he was a porowhita (circle). His aching sides and corners needed to be massaged in order to get rid of some of his pain. While lying on his puku reading the Geometers’ Weekly magazine, he spots his favourite sports hero, Jonah Trapz who is ‘built like a taparara’ (trapezium). Immediately, Tapatoru rite wishes he could transform himself into a taparara. But he needs your help.

2. As a possible way of introducing students to a trapezium, have them explore attributes of various trapezoidal shapes. Have them compare these with non-trapezoidal shapes including quadrilaterals that are parallelograms, rectangles, squares and others that are ‘nearly’ trapezoidal in shape. One approach is illustrated as follows:  
   Here is Hannah's work. She has sorted some quadrilateral shapes into two different categories: trapezia and not trapezia.

   Trapezia	Not Trapezia

   Hannah states that her sorting procedure is based on the relationship between one pair of sides. If just one pair of sides is parallel, then it’s a trapezium. The other pair of sides cannot be parallel.
   Do the parallel sides have to be different lengths? Why? (If the side lengths are equal then the other pair of sides will be parallel. The quadrilateral will be a parallelogram not a trapezium)

3. Ask the students to explore Hannah’s table of shapes and explain her sorting procedure.
   Ask questions that encourage the students to focus on quadrilaterals that have one pair of parallel sides. Some students might observe that a trapezium often looks like a triangle with the top cut off leaving an edge that is parallel to the side opposite.
4. Tapatoru rite (equilateral triangle) wants to look like his sports hero Jonah Trapz.
   Explore how you might fold Tapatoru rite (equilateral triangle) to make a taparara (trapezium). 
   The trapezium will contain three equilateral triangles within it, that are the same size.

5. Let students work on the challenge in pairs.
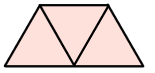
   The following diagram illustrates the change to a trapezium.
   

   Using the taparara (trapezium) that you have made:

   • How would you check that a pair of sides is parallel?
   • How would you use your understanding about the equilateral triangle to help you make a convincing argument for a pair of parallel sides?
   • How would you check that each of the smaller tapatoru rite are of equal size and shape, that is they are congruent?

Trapezium to rhombus

1. To go with his new shape, Tapatoru rite (equilateral triangle) changes his name to Taparara (trapezium). One day, he attempts to enter the Rhombus Exhibition at the Geometrical Museum - rhombi are one of Taparara’s favourite shapes. He is stopped at the door and told that only whakarara shapes (parallelograms) may go in. Taparara really wants to get in, so he decides to change shape. He doesn’t want to be just any whakarara, he wants to be a whakarara rite (rhombus). He needs your help.
2. Ask the students to fold Taparara to make a whakarara rite (rhombus). The following diagram illustrates the change from a trapezium to a rhombus:
   
3. Using the whakarara rite (rhombus) made ask:
   • How would you check that the sides are parallel?
   • How would you check that all the sides are of equal length?
   • What might the relationship be between the angle measure of the smaller corner and the angle measure of the larger corner? (Since the triangles are equilateral, the large interior angles of the rhombus are 60⁰ + 60⁰ = 120⁰)

4. Of course, Taparara changes his identity and name and becomes known as Whakarara rite (rhombus). Some of his friends call him Rhombus.

   Write two sentences that describe Whakarara rite’s appearance.
   What fraction of the original tapatoru rite (equilateral triangle) is Whakarara rite? (One half)

Session 4

Rhombus to a triangular pyramid

1. Once in the Geometrical Museum, Whakarara rite (rhombus) meets up with some of his friends, Tapawhā rite (square) and her sister Tapawhā hāngai (oblong).
2. At this point the students should do some personal research and write a report, using diagrams if needed, that illustrate the difference between the rhombus (whakarara rite), the square (tapawhā rite), and the oblong (tapawhā hāngai).
   Note that an oblong is a rectangle that is not a square. It has two pairs of parallel sides of different lengths, and four right angles.
3. Whakarara rite gets so excited by all the different diamond-like shapes that he folds into a particular diamond shape in ahu-toru (that is in 3 dimensions) called a koeko tapatoru (a triangular pyramid or tetrahedron). If you have a set of polyhedra, you will find a collection of pyramids. If not, locate a picture of one online).
4. By folding the whakarara rite (rhombus) out and in, turn him into a koeko tapatoru (tetrahedron).
5. The following diagram illustrates the change to a triangular pyramid.
    
   Koeko tapatoru is not a taparau (polygon) because he is no longer flat. He is three dimensional (ahu-toru).
6. How would you describe his appearance now?
   You might introduce some simple language of polyhedra, such as faces (flat surfaces), edges, and vertices (corners).

Triangular prism to hexagon

1. Koeko tapatoru (tetrahedron) stays like this for only a short time before changing back into a whakarara rite (rhombus). A little while later, Whakarara rite stops in at his favourite food place called Geo Flatworld Takeaways to get a kai of tapaono rite (regular hexagonal shape) chips.
2. Whakarara rite wants to fold into a tapaono rite (regular hexagon).
   Find a way of folding to make a tapaono rite that is made out of six equilateral triangles (e ono, tapa toru rite).
3. The following diagram illustrates the change to a tapaono rite.
    
4. Ask the students to check that it is a regular hexagon:
   Are all the sides equal? How do you know?
   Are all the angles equal? How do you know?
   What rotational and reflection symmetry does a tapaono rite have? (Six lines of reflective symmetry and rotational symmetry of order six)

Session 5

In the final session we reflect on the shapes that we have explored during the week.

1. At home Tapaono rite (regular hexagon) feels tired after a long day. He sits on the floor, closes his weary eyes, curls up into the frustum of a triangular pyramid and dreams about all the different shapes he was able to make ... with your expert help of course!
2. Tell the students that a frustum of any solid shape is made by making a cut parallel to the base and removing the top of the solid. Show them the example of the cone.
    
3. Get the students to explore how they might ‘curl’ their tapaono rite (regular hexagon) up so that they can make such a frustum.
4. Pose the following problems:
   Name the different shapes of the faces of your frustum.
   Make some statements about some of the attributes of the shapes that go to make up the frustum.
   If Tapaono rite (regular hexagon) had sides of length two, how long were the sides of the open top and the base of the frustum?

Teaching notes:

The following diagram illustrates how to change a hexagon into the frustum of a triangular pyramid.

Fold B to O, then A to O, then C to O to make a triangle shape. Lift the flaps so D and E touch, F and G touch and H and I touch.

The open top has sides of length two because these sides are the same as Tapaono rite’s sides. The base sides are of length three. You can find this by measuring. (If you are clever you can use right angled triangles to work it out without measuring.)

Session One

Begin each session in this unit with an exercise about in deriving from basic facts. Use a Slavonic Abacus to show how many different facts can be found from a given basic fact. Preferably use a physical abacus though virtual forms of the abacus are available online.

1. Model the multiples of five, or another basic fact that is appropriate to the knowledge of your students. Choose one set of multiplication basic facts to focus on throughout the session. The abacus below shows 6 x 5 = 30.
   
2. Begin with the first factor being even and relate the answers to multiples of ten.
   For example: 
   Why are the answers to 6 x 5 and 3 x 10 the same?
   Students might notice that two fives make one ten, which explains the doubling and halving effect. Otherwise, draw attention to the halving of 6, and the doubling of 5. Using proportional adjustments, such as doubling and halving or thirding and trebling, can make it easier to solve multiplication problems.
3. Make a sequential list of the even multiples of five (or of the other basic facts family you have chosen):
   2 x 5 = 10
   4 x 5 = 20
   6 x 5 = 30, etc.
   What does 0 x 5 equal? What does 10 x 5 equal? 12 x 5 equals?
4. Invite students to give facts that lie “between” the listed facts, e.g. 3 x 5 = 15 and lies between 2 x 5 and 4 x 5.
   You might encourage your students to remember the products if they do not already know them. Recite the facts in order, 1 x 5 =5, 2 x 5 = 10, 3 x 5 = 15, …etc. Erase two facts randomly each time and see if your students can recall the facts. Move to calling out particular facts for them to provide the product, e.g. “Seven multiplied by five.”
   Students could also be provided with whiteboards and asked to write down the facts individually or with a partner.
5. Start with a given fact, e.g. 6 x 5 = 30.
   If we know six multiplied by five equals 30, what other facts could we work out?
   Some examples might be:
                   
   5 x 5 = 25                                    7 x 5 = 35                                 6 x 4 = 24
                   
   6 x 6 = 36                                   6 x 7 = 42                                 12 x 5 = 60
   
   For each derived fact, show clearly how 6 x 5 is altered by moving beads on the abacus (as shown above).
    
6. Give students another known fact, e.g. 8 x 5 = 40.
   Tell them to create a spider’s web of facts that can be found using 8 x 5. Ask them to make as many connections as they can.
   For example:
   
   Share the students’ ideas and create a large whole class spider’s web of connections.
7. Move to the main investigation of the lesson (PowerPoint 1, Slide One)
   Mere has 60 kumara seedlings.
   She wants to space the plants out in straight rows.
   How many rows can she make? 
   How many seedlings will go in each row?
8. Let your students investigate the problem in pairs. Allow access to calculators for students who need extra support. Encourage recording of their solutions.
   How many different answers can you find?
9. Roam as your students work. Look for them to identify the problem as finding factors that multiply to a product of 60.
   Can you find all the possible answers?
10. Gather the class after an appropriate time. Aim to create a systematic list of possible ways Mere might plant her kumaras. There is no stipulation in the problem that the same number of seedlings are in each row. 
    Solutions like 12 + 8 + 12 + 8 + 12 + 8 and 7 + 5 + 6 + 6 + 8 + 4 + 9 + 3 + 10 + 2 are acceptable (the addends are the number of seedlings in each row). These strategies usually have a system involved. For example, the last set of addends seems to be based on 12 (7 + 5, 6 + 6, etc.). Concentrate on solutions in which the numbers of plants in a row are equal. As students offer solutions organise your recording like this:
    
11. Ask: Are there answers ‘in between’ the solutions we have?
    Students might try out three rows, four rows, seven rows etc. to see if that number of rows will work. A calculator might prove useful to find missing solutions. You could discuss simple divisibility rules, e.g. the digits of numbers divisible by three always add to a multiple of three, 54 ÷ 3 = 18 (divisible) and 5 + 4 = 9 (a multiple of three).
12. What operation will you key in?
    Division is efficient while multiplication requires a bit of trial and error, e.g. 60 ÷ 8 = 7.5 which is preferable to 8 x 6 = 48, 8 x 7 = 56, 8 x 8 = 64,… Aim to get a full set of factors for 60. Note that each pair of factors, such as 5 x 12, gives two solutions to Mere’s problem, e.g. 5 rows of 12 plants or 12 rows of 5 plants.
13. Slide Two of PowerPoint 1 extends the problem:
    After Mere has planted her 60 seedlings Uncle Rewa gives her 12 more.
    “That works out okay,” she says, “I’ll just put more plants in each row.”
    Which of the previous solutions will still work if 12 plants are added?
14. Let students work on the amended problem. 
    Do they recognise for a solution to be built on, at least one existing factor must be a factor of 12? 
    For example, 2 rows of 30 plants cannot be changed to “3 rows of …” but it can be changed to 2 rows of 36 plants. 5 rows of 12 plants can be changed to 6 rows of 12 plants.
    Come up with a list of solutions; 1 row of 72, 2 rows of 36, …, 6 rows of 12.
    Are there any ways to plant 72 kumara seedlings in equal rows that are not on our list?
    Students might identify 8 rows of 9 and 9 rows of 8 but these options cannot be created from the solutions for 60 plants without transplanting.
15. Ask students to reflect on important words they have encountered, particularly "factor", and "product". They could write a definition for each word in their book, or you could add the class-created definition to the PowerPoint. Also ask them to take a specific equation, such as 4 x 15 = 60 and explain the meaning of the symbols x and = with a partner. Pair up students with different levels of mathematical knowledge to encourage tuakana-teina. 

Session Two

1. In the introduction of the lesson use the Slavonic Abacus to connect the “ _ multiplied by ten” facts to the “_ multiplied by nine” facts. For example:
                  
   6 x 10 = 60                            so           6 x 9 = 54 (Six less)
    
2. Develop a set of “nine times” facts, e.g. four times nine equals 36 (4 x 9 = 36). Look for patterns in the list of facts.
   Can you find patterns in the set of nine times facts?
   1 x 9 = 9
   2 x 9 = 18
   3 x 9 = 29
   …
   9 x 9 = 81
   10 x 9 = 90
   Students might notice these patterns:
   In the products the tens digits go up by one while the ones digits go down by one.
   The multiplier is always one less than the tens digit in the product, e.g. In 8 x 9 = 72, 7 is one less than 8.
   The digits in the product always add to nine, e.g. 4 x 9 = 36, 3 + 6 = 9.
3. Encourage students to think about why the patterns happen.
4. Work towards memorising the times nine facts by reciting them, creating flash cards and practising. There are many sites on the internet for practising basic facts and you can use the basic facts tool on e-ako maths as well. 
5. Move on to the main problem of the lesson (Slide Three of PowerPoint 1). Is worthwhile to act out the problem with the students first. Use counters, cubes, or other objects to be cookies, with different colours used for each flavour.
6. Ask the students to solve the problem in small groups of two or three. It is important that they record their mathematical thinking, both to support their work and as an artefact that can be shared with other students. As you roam look for your students to:
   • Recognise and honour all the conditions of the problem, e.g. all plates the same, all cookies exhausted.
   • Use multiplication facts to support them trial possible compositions for the plates. Note that access to a multiplication facts chart, or calculator might be needed to give access for some students.
   • Realise that common factors of 24, 36 and 48 are important to the problem.
   • Work beyond a single solution to consider all the possible solutions. Note that students should decide which of possible plate compositions will be the most useful for selling at a fundraising event.
7. After a suitable time, gather the class to share ideas. Discuss useful strategies and connect those strategies to important vocabulary such as factor, and multiple. Relate the action of sharing equally to division. For example:
   Will eight plates work? Why? Why not?
   24 ÷ 8 = 3, 36 ÷ 8 = 4 r4 or 4 ½, 48 ÷ 8 = 6. Therefore, eight plates will only work if some cookies are not used or are cut into halves. One strategy breaks a condition and the other will ruin the presentation of each plate.
8. Discuss: How can we find the number of plates that might work?
   Two plates will work because 24, 36 and 48 divide equally by two. Each plate might be too big to sell.
   Three plates will work because 24, 36 and 48 divide equally by three. Each plate might be too big to sell.

9. Discuss:What is a good strategy to see if a certain number of plates will work?
   Will five plates work?Why? Why not?
   Five plates will not work as 24, 36, and 48 are not divisible by five (not in the five times table).
   Will six plates work?  What about seven plates? Etc.
   Some students might list all the factors of 24, 36, and 48 to see what numbers of plates might work. You might give the students the start of the table and ask them to complete it.

   Number of Plates

   1

   2

   3

   4

   5

   6

   7

   8

   9

   10

   11

   12

   24 raisin

   ●

   ●

   ●

   ●

   ●

   ●

   ●

   48 oatmeal

   ●

   ●

   ●

   ●

   ●

   ●

   ●

   36 chocolate

   ●

   ●

   ●

   ●

   ●

   ●

   ●

10. Discuss: Should we stop at 12 plates? Are there other numbers of plates that might work?
    If we use six plates, how many of each cookie is on each plate?
    If we use twelve plates, how many of each cookie is on each plate?
    Can we work this out from the six plate answer? How?
11. Make a collective decision about the best answer, given the context.
    Six plates with 4 raisin, 8 oatmeal, and 6 chocolate cookies is probably the most practical.
12. You might vary the cookie problem by changing the numbers. For example, 25 raisin cookies, 35 oatmeal cookies, and 45 chocolate cookies.
13. Introduce the hiking and cycling problem on Slide Four of PowerPoint 1. Act out what is meant by rates of 3 kilometres per hour and 7 kilometres per hour. Students will be familiar with cars travelling at 100 or 50 kilometres per hour. Use car travel as a helpful context.
14. Let students attempt the problem individually or in small groups. Roam the room and look for:
    • Do they use the rate as the unit of measurement? For example, the walking time can be calculated by 25 ÷ 3 = 8 r1 or 8 1/3 hours.
    • Do they see similarities between the cookie problem and the walking/hiking problem?
15. Gather the class and discuss solution strategies. You might use a double number line to organise the information in the problem.
    A double number line of Nico’s hike looks like this:
    
16. Build up the first few time and distance pairs, (1,3), (2,6), (3,9),...
    Is there an easier way to predict the amount of time Nico will take?
    Students might see that multiplying the time, in hours, by three gives the distance that Nico hikes, in kilometres. 8 x 3 =24 so it takes Nico over eight hours. Some students might be able to get more precise. 
    If Nico hikes 3 kilometres each hour,how long will it take him to hike 1 kilometre? (1/3 of an hour or 20 minutes)
17. A double number line for Kat’s cycle looks like this:
    
    Build up the time and distance pairs in a similar way, (1,7), (2,14), (3,21),... Can students see that multiplying the time, in hours, by seven gives the distance, in kilometres?
    Can they be more precise than saying that “Kat takes over 8 hours to cycle 48 kilometres”? (two kilometres takes her 2/7 of an hour. That’s less than one third and equals about 17 minutes.)
18. You might change the conditions of the Nico and Kat problem to make it easier or harder, and to see if students have generalised how to solve simple rate problems. For example:
    Niko is hiking a 30 kilometre track. 
    He can walk at about 4 kilometres per hour, including rest stops. 
    Kat is cycling a 45 kilometre trail . 
    She rides at about 6 kilometres per hour, including rest stops.

Session Three

1. The introduction of this lesson involves repeated doubling to connect multiplying by two, four and eight. Start simply with 2 x 3 then 4 x 3 then 8 x 3.
                  
   2 x 3 = 6                                      4 x 3 = 12                                  8 x 3 = 24             
   
   What patterns can you see?
   Students should notice that the product doubles as the multiplier doubles.
   What multiplication fact would come next? 
   (16 x 3 = 48. You might need two abacuses to show that)
    
2. Introduce another example such as 2 x 6 (six multiplied by two) then 4 x 6 then 8 x 6. Ask students to find the total number of beads each time:
                      
   2 x 6 =12                                        4 x 6 = 24                                   8 x 6 = 48
   What patterns can you see?
    
3. Give students some examples to solve without the abacus model. For example:
   2 x 4 = 8, so 4 x 4 = ____, so 8 x 4 = ____, so 16 x 4 = ____
   2 x 8 = ____, so 4 x 8 = ____, so 8 x 8 = ____, so 16 x 8 = 
   7 x 2 = ____, so 7 x 4 = ____, so 7 x 8 = ____, so 7 x 16 =
   2 x 11 = ____, so 4 x 11 = ____, so 8 x 11 = ____, so 16 x 11 =
4. Introduce the game Dicey Times to your students using slides 5 and 6 for PowerPoint 1. The aim of the game is to place the dice numbers in the circles to maximise the score. The points for each circle come from how many of the numbers in a row, diagonal  or column are multiples of the dice number.
5. Copymaster 1 provides the grid shown in PowerPoint 1 and another simpler set on the first page. The second page provides blank grids for you to enter new numbers or for the students to create their own grid.
   Note that a simplified form of the game is available using this Figure It Out task: Dicey Dabble.
6. As students play the game a few times look to see that they:
   • Recognise that strategic choice about where to locate the dice number improves their chance of winning.
   • Scanning each row, column and diagonal for common multiples helps locate the best spot for a given dice number.
   • Notice that a dice number of 1 gives 4 points whichever row, column or diagonal it is located on.
   • Some numbers, like 17 and 23, are multiples of only one. They are prime numbers. Locating a dice number of 1 is the only way to get points from these numbers in the grid.
7. Gather the class and use slide seven of PowerPoint 1 to play a virtual game together. Discuss the best circle to locate each dice numbers and why that circle is best. Try to bring out the teaching points above.

Session Four

1. Begin the session with deriving the “multiplied by six” and “multiplied by seven” facts from the “multiplied by five” facts. The pattern involves the distributive property of whole numbers under multiplication.
   Use this example first:
                 
   4 x 5 = 20                                 4 x 6 =                                      4 x 7 =
    
2. Use 8 x 5 next:
               
   8 x 5 = 40                                  8 x 6 =                                      8 x 7 =
    
3. Provide students with three different “multiplied by five” facts and ask them to draw a spider web of related facts. For example, the web for 6 x 5 = 30 might have arms of 6 x 6 = 36, 6 x 7 = 42, 6 x 4 = 24, 3 x 10 = 30, 6 x 50 = 300,  6 x 8 = 48, 5 x 6 = 30, etc.
4. After students create their webs, pair them with another student to compare their facts.
   Can you make your spider web even larger?
5. Use Slide 7 of PowerPoint 1 to discuss four different sports. You may need to hunt for short clips online if students are not familiar with how the games are played.
   Suppose we decide to run a sports day. 
   Each sport is on at a particular time of the day. 
   No other sport is played at that time. It is too hard to organise.
   We want as few players as possible that are reserves at any time. Everyone must be in a team.
   What is the ideal number of entries (people) for the sports day?
   Explain your answer.
6. Let your students work in small teams to solve the problem. Encourage them to record their thinking so they can explain their solution to the whole class.
7. Roam the room as teams work looking for the following:
   • Use of multiples to find the best numbers of players for each sport.
   • Scanning for common multiples to find a number of players that works well for many sports.
   • Recognition that multiples of 4 are in multiples of 8, and multiples of 5 are in multiples of 10.
8. The last point simplifies the problem a lot as students need to find a number of players that is a multiple of 8 and 10. The smallest number that fits is 40 players though students may suggest numbers like 80 that also work. In fact, any multiple of 40 will work.
9. Gather the class to discuss students’ strategies, highlighting the points above. Introduce Slide 8 to add more complexity. All the sports on Slide Seven are still being played but introduce Petanque (3 players per team), Volleyball (6 players per team), and Softball (9 players per team). 
   How many players will we need at the Sports Day if we include these sports as well?
   This task is very challenging but students will have some idea of how to approach it from the earlier problem. Make calculators available as the focus is on thinking with multiples, not  on calculation.
10. Let students work in small teams again. Roam to room and look for students to:
    • Recognise the need for common multiples.
    • Recognise that the number of players must be a multiple of 40 (from the previous sports).
    • Realise that numbers of players for softball (multiples of 9) will also work for Petanque (multiples of 3). Even multiples of 9 also are multiples of 6.
      The easiest solution is to multiply 40 by nine. 360 is divisible by 8, 10 and 9, which is required for there to be no reserves at any time.

Session Five

1. Use the final session as an opportunity for students to demonstrate their growing multiplicative thinking. Ask them to choose from the following tasks from the Figure It Out series. 
   • The Hundreds Board Hunt from Multiplicative Thinking, Level 3.
   • Multiples and Factors, from Multiplicative Thinking, Level 3.
   • Fun Rides, from Number, Level 3.
   • Busking Blues, from Number, Level 3
   • , Book Two.
   • That Old?, from Number, Level 3, B
   • , Book Three. Easy Nines, from Number, Level 3, Book Three.
   • Movie Maths, from Number, Level 3ook Two.
   •  
2. Use the opportunity to roam the room and assess students’ achievement of the learning outcomes.

Session 1: Sugar Boxes

In this session we design boxes to hold 64 sugar cubes.

Resources

• Multilink cubes
• Rulers: 30cm and one metre

1. The Sweet-tooth Company has hired you to design rectangular boxes to hold 64 cubes. Each cube has edges of 2 cm, just like multilink cubes. What sizes of boxes could they have? Sketch rough plans for boxes that can hold 64 sugar cubes, showing the length, width, and height of each box. Consider sketching a design as a class, and then giving students opportunities to draw their own.
2. How many different boxes could be made? How could this be worked out without having to build each shape with cubes?

Possible boxes include:
2cm x 2cm x 128cm for 64 cubes in a single row
4cm x 2cm x 64cm for 2 rows of 32 cubes
8cm x 4cm x 16cm for 2 layers, each with 4 rows of 8 cubes

Session 2: Toothpaste boxes

In this session we explore the size of commercial boxes and construct a rectangular box (cuboid) of a given size.

Resources

• Small cardboard boxes from home of different sizes (e.g. toothpaste, cocoa, spice, small woven harakeke (flax) containers)
• Place-value blocks
• Centimetre squared paper
• Scissors, tape, glue
• 30cm rulers

1. How many cubic centimetres (small place-value block cubes) can fit exactly into each box? (There must be no gaps or over-filling.)
   The students may choose to work this out by filling each box with place-value cubes, but is there an easier way?
2. You are told that a packet can hold 1000 small place value blocks cubes, which is 1000 cubic centimetres, or 1 litre. How big might the packet be? Make the packet from centimetre square paper.

Session 3: Box capacity

In this session we find the capacity of boxes in millilitres and cubic centimetres. The task in this session could be introduced as the teacher modelling to the whole class. Then, students could work in pairs or small groups to estimate and measure the capacity of the different containers. Students could record their estimates and measurements on mini whiteboards or in a table.

Resources

• Boxes from session 2
• Small plastic bags
• Capacity measures

1. Use the boxes from session two. Find out how much water, in millilitres, each packet can hold. This can be done in the following way. Push a small plastic bag snugly into the packet (make sure it does not have holes!). Pour water into the bag until the top of the packet is reached. Pull the bag gently out of the packet. Estimate the capacity of the container. Pour the water into a measuring container to measure the capacity.
   Compare the estimates and measurements - consider why they are different or similar
2. Compare the capacity of each box, in millilitres, with its volume in cubic centimetres. What do you notice? Is there a pattern that is the same for each box?

Session 4: The metre cube

In this session we find the number of place-value blocks that fill a metre cube. This task could be completed as a whole class introduction to the size of a metre cube. To reinforce learning, students could estimate how many metre cubes might fit in different classrooms or spaces around the school.

Resources

• Metre rulers
• Place value blocks
• Newspaper
• Tape, scissors

1. Using a metre ruler, rolled up newspaper, and tape make the skeleton of a cube with edges of one metre. This is a cubic metre.
2. How many large place-value block cubes (1000 cm³ or 1 litre) would fill the metre cube?
3. How many flats, longs and small cubes would fill the cubic metre?

Session 5: Air space

In this session we investigate the capacity of the classroom.

Resources

• Cubic metres from session four

1. Use the newspaper cubic metres that you made in session four to help you in this activity.
2. Your classroom needs a new air-conditioning unit to keep the class warm in winter and cool in summer. It is important to find out how many cubic metres of air space there is in your classroom so that the correct unit can be bought. Work out the air space of your classroom in cubic metres and write a short report to your principal explaining how you worked it out. As an extension activity you might work out the air space of the hall. How many times would your classroom fit into the hall?

Session 1

In this session students use the clues provided to find out the prices of items on a menu. The clues involve applying addition and subtraction with unknowns.

1. Show your students Copymaster 1, ideally on an interactive whiteboard or other large screen.
   Here is the menu from the Cafeteria at Kiwi School. 
   What is a cafeteria?
   What is meant by daily specials on this menu? (A cycle of options available on days of the week)
   Explain what is meant by Regular Daily Items? (Items that are always on sale, no matter the day of the week)
   Ensure that students know what is meant by snacks and drinks.
    
2. Invite students to imagine they are at Kiwi School and need to order their lunch for today. 
   Give them some time to decide on their preferences, using the provided menu, and to record those preferences. During this, links could be made to the Food and Nutrition Area of the Health and Physical Education section in the New Zealand Curriculum.
    
3. Share some choices with the whole class.
   How much will you pay for your lunch today?
   Students may notice that the prices are not visible.
   Luckily we have a set of clues to help us work the prices. Before we start, can someone clarify what a combo is.
   Ensure that students recognise "combo" is short for combination.
   What is a combination?
    
4. Discuss how food sellers use combos to entice customers to buy several items at a discounted price. At this stage, you could make links to food combos that students order in their local community (e.g. two pieces of fish and one scoop of chips). You might discuss why students choose to order combos rather than separate items (e.g. convenience, price)
5. Use PowerPoint 1 to work through the clues. Ensure that students have access to the list of food items (Copymaster 1) during this discussion. Discuss the following points:
   • Clue One: If the cost of two choices is $5.00 what might one choice and three choices cost?
     What are the possible options for one choice and three choices?
     How could we organise those possibilities?
     Ask students to write some possibilities on their copy of the menu, e.g. $1.00 and $2.00, $2.00 and $4.00, $3.00 and $6.00, etc. 
     Which possibilities are unlikely?
     One choice must be cheaper than two choices otherwise people would not buy one choice. 
     Must the prices be whole dollars? What does that mean for the possibilities?
     Since there are a huge range of possibilities it might be better to write a rule, like 2 x, to show the relationship. Watch to see how your students record their rule.
   • Clue Two: Does that tell you the cost of one daily item? How?
     If two daily items cost $5.00 then each item must cost $2.50.
   • Clue Three: How can we work out the cost of one snack and one beverage? 
     $2.50 - $1.00 = $1.50 is the cost of one snack and $2.50 – $0.50 = $2.00 is the cost of one beverage.
   • Clue Four: How can we use this clue to work out the cost of the daily specials?
     3 x $2.00 = $6:00 so the cost of three choices equals $6.00
     What is the cost of one choice?
     Record [ ] x 2 = $6.00 so [ ] = ? ($3.00 - cost of one choice)
      
6. The other slides on PowerPoint 1 give clues to work out the cost of combos. Let your students work through the clues in pairs. You may choose to pair up more knowledgeable students with less knowledgeable to encourage tuakana-teina and collaboration. Look to see that students:
   • Use the menu to organise the data as they work through clues.
   • Calculate accurately and fluently with the money amounts.
   • Accept when unknowns must be reasoned with, even when the value is unknown.
      
7. After a suitable time, bring the class together to share the students’ solutions. Ask students to justify how they got their answers. You may support students by working through the answers to each question as a group. Materials (e.g. laminated or digital number lines) could also be used to model working.
   Combo 1: $6.50                 Combo 2: $7.50                 Combo 3: $8.00                 Combo 4: $3.00
   Remind them to order the lunch they chose and calculate the cost of it.
   Was it cheaper for you to order a Combo?
    
8. Discuss the situations in the task when the actual values were not known.
   For example, Combo 2 and Combo 4 cost a total of $10.50.
   How did you record that clue?
   Students might have drawn arrows connecting the Combos on the menu, or have other strategies. 
   Record: C2 + C4 = 10.5
   What might that equation mean?
   I could record the same relationship as ○ + □ = 10.5
   Which way do you think is better?
   The key point is that the meaning of the symbols needs to be clear. It is good practice mathematically to define what both symbols represent. It may be useful to decide on specific symbols to use, as a group. 
   How might you record the clues, “One snack costs $1.00 less than one daily item, and one beverage costs 50 cents less than one daily item”?
   Students might invent notation like; s = d - 1 and b = d – 0.5 or use ‘empty’ shapes instead of the letters.

Session Two

In this session students explore "change" and "start" unknown addition and subtraction problems. They should record their solution strategies as equations with specific unknowns, and should recognise when either addition or subtraction can be used to solve a problem.

1. The staff at Kiwi School Cafeteria think that some prices need to go up because the cost of the food has increased. They also think that some prices should go down as students and teachers are not buying some items.
    
2. Here are some examples:
   The new price of regular daily items is $3.40.
   What was the old price?
   What is the price increase?
   Let students solve the problem in pairs before sharing their strategies as a whole class.
   Use words, equations, and empty number lines to record their strategies.
   By change unknown addition:
   “$2.50 add what equals $3.40?”
   2.50 + [ ] = 3.40
   
   Students are likely to find the change in incremental jumps, like this, with $3.00 used as a benchmark.
   
   If no students use subtraction to solve the problem, you might model a solution as:
   “$3.40 subtract $2.50 equals what?”
   3.40 - 2.50 = [ ] 
   
   Which strategy is the most efficient for the problem? (Addition is much easier).
   Encourage students to justify why they think one strategy is more efficient.
    
3. Pose price drop problems like:
   The new price of Combo 2 is $6.80.
   What was the old price?
   What is the price decrease?
   This problem is a change unknown subtraction problem that can be represented as:
   “$7.50 subtract what equals $6.80”
   7.50 - [ ] = 6.80
   
   Students are likely to use incremental jumps to find the missing number (subtrahend).
   
   Could the problem be solved using addition?
   The use of change unknown addition looks like this:
   “$6.80 add what equals $7.50?”
   6.80 + [ ] = 7.50
   
    
4. Provide your students with Copymaster 2 that contains a range of problems for them to represent and solve. You could supplement these with problems that reflect the context of your classroom. For example, links could be made to food being sold at the Hokitika Wild Foods Festival, or the Moana Nui Festival. More knowledgeable students could also design their own questions to present to the class. 
    
5. After an appropriate time, gather the class to share solutions. 
   Highlight the use of equations and empty number lines as recording strategies.

Answers to Copymaster questions:

1. 1.50 - [ ] = 0.90 or 0.90 + [ ] = 1.50. The price has decreased by $0.60.
2. 2.00 - [ ] = 1.30 or 1.30 + [ ] = 2.00. The price has decreased by $0.70.
3. Answers will vary but 0.80 + 1.40 = 2.20 so $2.00 is a good new price for Combo 4.
4. The price increases are one choice ($0.70), two choices ($1.40), and three choices ($2.10). There is a consistent increase of $0.70 per choice.
5. The old price of the combo had a discount of $1.50.
   Adding the new prices and applying that discount gives:
   3.70 + 3.40 + 0.90 + 1.30 – 1.50 = $7.80
   Other answers are possible.
6. The equation is [ ] - 0.80 = 2.50 or 2.50 + 0.80 = [ ]. The previous price for one pie was $3.30.

Session Three

In this session students represent change and start unknown problems with multiplication and division. They do so in the context of the Kiwi School Cafeteria used in the previous two lessons. The focus in this session is more on making sensible decisions about the operations to perform than on strategies for calculation. ‘Unfriendly’ amounts are used for the prices and students are required to choose appropriate operations to solve the problems.

1. Begin with the Cafeteria Manager’s problem. Give your students Copymaster 3 which has the menu with updated prices.
   The Manager sees that Room 7 ordered $17.00 worth of Regular Daily item 1, the stuffed potato. The class monitor has not written how many potatoes are ordered. 
   How can the manager work out how many potatoes to send to Room 7?
   What information do we need to solve this problem? (The price of Regular Daily Items is $3.40 each)
   What operation do we need to perform?
   Students might realise that they need to answer “$3.40 multiplied by what number equals $17.00?”
   How can this problem be written as an equation? ([ ] x 3.40 = 17.00)
   Is there another operation that might be used? 
   What would the equation for that operation be? (17 ÷ [ ] = 3.40 ($17.00 shared into how many equal amounts equals $3.40?) or  17.00 ÷ 3.40 = [ ]($17.00 measured in amounts of $3.40 gives how many amounts?))
   The second option for division gives a direct answer of five items. Let students use a calculator to find their answer then use five as the unknown in the other two equations.
   5 x 3.40 = 17.00 (The calculator will not show whole number amounts with a decimal point)
   17 ÷ 5 = 3.40
    
2. Point out that the manager faced even harder problems when monitors did not record the orders correctly.
   One day a single order came in from Room 2.  The total amount was $25.90 and the form said “7x”. The manager knew that each student had ordered the same kind of item but what was it?
   What does 7x mean on the order? (Seven, of the same item, are ordered)
   What equations could we use to record the problem?
   How could the manager work out what kind of item was ordered?
   7 x [ ] = 25.90          25.90 ÷ 7 = [ ] 
   Use the equations to find out what kind of items were ordered.
   Students might use the multiplication equation but that involves a trial and error process until the correct amount is found, e.g. 7 x 4.00 = 28.00, 7 x 3.00 = 21.00, etc. The division equation gives a direct answer. Substitute the answer back into the unknown in the multiplication equation to verify that both equations give the same result for the unknown, $3.70.
   What type of item is this order for? (One Choice Daily Specials)
    
3. Some problems for the manager are when the total cost is missing.
   For example: 
   Room 12 sends in an order for 9 students who want to buy Combo 2 at $7.80 each.
   The manager checks to see that the money inside the class envelope is correct.
   How much money should there be?
   Students will probably recognise that this is a result unknown multiplication problem.
   What equations can you write to represent this problem?
   9 x 7.80 = [ ]
   How could we write the same problem as division?
   [ ] ÷ 7.80 = 9 or [ ] ÷ 9 = 7.80
   Discuss what each equation means, e.g. “The unknown total amount shared among the nine orders equals $7.80 for each order?”
   Which way to record the problem is the most sensible? 
   Clearly the multiplication gives a direct answer, of $70.20.
    
4. Give students Copymaster 4 to share among a group of three students.
   • Students cut up the cards and put the six order cards in separate places.
   • Students assign the equation to the order card that matches it.
   • Students choose six different cards and record the problem that the equation solves, e.g. The order for Room 3 totals $115.20. Each pairing of Daily Specials items costs $6.40. How many two-special items are ordered?
      
5. Discuss the responses to part c. 
   Can students explain the use of numbers and operation in the problem they write?
   In particular, observe that they understand the difference between sharing and measurement division.

Session Four

In this session students explore situations in which more than one operation is involved, and they learn to discriminate between additive and multiplicative situations. To allow for more flexibility the context is changed from a canteen to a fruit and vegetable store. At this stage, the context could be changed to further reflect the cultural diversity of your students. For example, students could remake Copymaster 5 with foods of their choice, and use the provided questions to plan a menu for a shared celebration involving kai. An investigation into traditional hākari (feasts) could ignite interest in this learning. In te ao Māori, different times of the year (e.g. the kūmara harvest in March) were celebrated with different hākari. To extend more knowledgeable students, hardcopy (or online) supermarket pamphlets could be used to provide more complex numbers for the different food items.

1. Give students a copy of Copymaster 5 to share in pairs. Pose this problem:
   Imagine you go to Pip’s Fruit and Vege Shop with $20.00 in total to spend. You must buy at least two different foods. 
   What will you buy? 
   How will you calculate the total cost?
   What change will you get?
    
2. Allow the pairs sufficient time to create an answer. You might provide a calculator for some students as the emphasis is on choice of operation rather than calculation strategies. For other students, the task provides an excellent opportunity for the mental calculation they are likely to use in real life.
    
3. Share students’ answers in this way:
   Record the operations you performed to get your total cost. We will try to figure out what you bought.
   For example, a pair of students might record 1.5 x 2.79 + 3 x 1.99 + 2.4 x 3.70 = $19.04.
   Students might work out that they bought 1.5kg of bananas, 3 avocados, and 2.4 kg of apples.
    
4. After a period of sharing, pose more demanding problems that involve several operations. Here are some possibilities with answers:
   Tim and Iti spent a total of $17.50. 
   They bought 3.5 kg of mandarins and an amount of onions.
   How many kilograms of onions did they buy? 
   An equation might look like this:
   3.5 x 2.65 + [ ] x 2.75 = 17.50
   How can we work out the amount that Tim and Iti spent on onions? (Subtract 17.50 – (3.5 x 2.65) = 8.23 (rounded))
   What operation will tell us how many kilograms of onions they bought? (8.3 ÷ 2.75 = 2.99)
   Tim and Iti bought about 3kg of onions.
    
5. Petra and Josefa bought 2.3 kg of beans and 5 kg of potatoes. How much more did the beans cost than the potatoes?
   An equation might look like this:
   2.3 x 4.50 - 5 x 1.35 = [ ]
   Notice that a difference is found by subtraction or adding on.
   5 x 1.35 + [ ] = 2.3 x 4.50
   In this case subtraction gives direct access to the difference of $3.60.
    
6. Lana and Tyrese bought 4 kilograms of fruit. 
   They bought 2 kilograms each of two different fruit. The total cost was $13.10. 
   What fruit did they buy? 
   An equation might look like this:
   2 x [ ] + 2 x ( ) = 13.10
   How can we find the total cost of 1 kilogram of each fruit? (divide by two)
   [ ] + ( ) = 6.55
   What two fruit prices match $6.55 per kilogram? 
   Students might realise that one price will need to have 5 in the hundredths place while the other must have 0 in the hundredths place. Only kiwifruit and plums will work.
    
7. Ask your students to pose their own multi-operation problems for another pair to solve. The problems they create might be collected into a book of problems about Pip’s Shop.
    
8. Roam as students create their problems.
   How adventurous are they in combining the operations? (Do they stay in safe territory with addition and subtraction, or multiplication and division?)
   Do they provide a solution to their problem showing the steps as equations?
    
9. After students spend an appropriate time creating problems change the focus to which operation to use. Copymaster 6 has several problems designed to see if students can make appropriate decisions about the operation/s to use.
    
10. Allow students sufficient time to solve the problems in pairs then discuss the solutions as a class. Drawing diagrams and acting out the problems may support some students to develop solutions. Below are notes on each problem:
    1. The difference in price is constant thought students are not told what that amount is. In February kiwifruit cost 12 ÷ 3 = $4 per kilogram while apples cost 9 ÷ 3 = $3 per kilogram. The price difference is always $1 per kilogram.
       In May apples cost $15 ÷ 3 = $5 per kilogram. Therefore, the price of kiwifruit is $5 + $1 = $6 per kilogram.
    2. The basket costs $8.00 but the cost of the fruit equals (17 – 8) ÷ 3 = $3 per kilogram. A fruit basket with 5 kilograms of fruits will cost 5 x 3 + 8 = $23.
    3. Each kilogram of mandarin costs 11 ÷ 4 = $2.75. 10 x 2.75 = $27.50 is the cost of 10 kilograms.
    4. This is a constant problem. Every person takes 2 minutes to eat an orange. 24 people who begin eating at the same time will take the same amount of time, 2 minutes, to eat one orange each.
    5. There is not enough information to solve this problem but there are two possible answers.
       If Nashi pears cost more than plums, then mangoes cost 2.50 + 1.75 = $4.25 per kilogram than plums.
       If plums cost more than Nashi pears, then mangoes cost 2.50 - 1.75 = $0.75 per kilogram than plums.
    6. If the amount of both nectarines and peaches is halved, then the difference is also halved.
       3.60 ÷ 2 = $1.80.

Getting Started

1. Fold a circle in half and cut pieces out of it in any way you like. Ask the students to anticipate the pattern that the opened-up shape might have. Write down any mathematical vocabulary that might arise, in particular, terms like symmetry, or reflection. Open the cut circle to confirm the students’ predictions. The shape has reflective or line symmetry along the fold line. 
   
   What pattern can you see in the shape?
   How did the way we made the shape affect the symmetry it has?
   You may want to show how the whole shape is visible if the mirror is located along the fold line. 
   Mirror symmetry and fold symmetry have the same meaning with 2-dimensional shapes.
2. Ask: Why is reflective symmetry sometimes called mirror symmetry, fold symmetry, and flip symmetry?
   It is important for students to see that one half of the shape maps onto the other half by folding and flipping actions. Each alternative term can be demonstrated. Holding a mirror along the fold line enables students to see an image of the whole shape even when one half is masked. Similarly, the amended (cut) circle can be refolded in half and traced around. Then flip the paper over the fold line and trace around it again. The traced figure will be that of the whole amended circle.
3. Ask students to make their own shape by folding a circle in half and cutting out pieces (they must not cut all the way along the fold line). This will enable them to conjecture that all such shapes have at least one line of reflective symmetry (some may have two depending on the cuts). The symmetric shapes may be displayed on a chart.
4. Move onto folding a circle into quarters (in half then in half again) and cutting pieces out. 
   
   Before opening up the circle ask:
   What pattern do you expect the shape to have?
5. Confirm that the two fold lines are lines of reflective symmetry.
   Is there another type of pattern in this shape?
   Students may not recognise that the cutout shape has rotational symmetry as well. Trace around the shape on a whiteboard. Turn the shape one half turn (180⁰) to show that the shape maps onto itself.
   The shape has half turn symmetry. How many times will it map onto itself in a full turn?
   Students should predict order 2 rotational symmetry. That means the shape maps onto itself twice, in a full turn.
6. Ask students to create their own pattern using quarter folds of a circle. Ask them to compare their shape with that of a partner. 
   How are the shapes the same? How are they different?
   Do both shapes have the same symmetry?
   Most students will realise that there are two lines of reflective symmetry (the fold lines) but the half turn rotational symmetry is harder to spot.
7. Ask your students to anticipate then investigate what symmetry the circle shape will have if folded in eighths or sixths before cutting. Sixths can be created by folding the circle in half and then looping the half into thirds (see diagram below). (The circle folded into eighths will have at least four lines of reflection symmetry and rotational symmetry of order 4; with sixths the symmetry is six lines and order 3). Ask the students if they can see a pattern in the "least number" of lines and orders.
   
    
8. Challenge the students to use paper circles to create a shape that has rotational symmetry of order 3 but no lines of reflective symmetry. Next ask them to produce a shape that has rotational symmetry of order 4 but with no lines of reflective symmetry. Then ask for a shape that has rotational symmetry of order 5 with no lines of reflective symmetry, etc.

Session Two: Car logos

1. Begin by showing a short film clip of a car from a popular brand.
   What make of car was that?
   How do you know?
2. Investigate the logos found on motor vehicles by looking at cars in the school car park, magazine advertisements or images from the internet. PowerPoint 1 provides some common car logos. Car advertisements in magazines can also be cut out and used. Most manufacturers use symmetry of some kind in designing their logos. For example, Audi uses four intersecting circles in a line. This pattern has one line of reflection symmetry. This logo is created by translating (shifting) one circle three times.
   
3. Discuss the symmetry of each logo and compile a list of car manufacturing companies for future reference. (You may need to omit the manufacturer’s name from some of the logos to get any symmetry. For instance, removing ‘Ford’ from its logo gives an elliptical shape that has two lines of symmetry.) It is just as important to identify logos that are non-examples of symmetry. For example, the logos for Volvo and Jaguar, and Peugeot have no symmetry, even when the company name is removed.
   
4. Provide the students with drawing instruments such as rulers, protractors, drawing compasses, or jar lids, and tell them to recreate the car logos they saw in the car park, online or in magazines. Have the images available for them to refer to, if needed. At times it may be necessary to bring the class together to discuss construction skills. For example, for a logo involving rotational symmetry of order 3, a protractor will be useful. Since there are 360° in a full turn, one third of that is 120°, which gives the angle measured at the centre for dividing a circle in thirds. Construction skills like drawing a right angle by using a protractor or compass construction may be modelled if necessary.

Session Three: Logos in the media

1. As homework (see Homelink) ask the students to find other examples of logos. Obviously not all logos have symmetry. Sporting goods manufacturers are good examples of this. Nike uses a “swish” that was designed to embody movement. Adidas uses three stripes etc. Examples will illustrate to the students that logos have to be both aesthetically pleasing (i.e. often symmetric) and suggestive of the nature of the company. Share the logos students bring along and group them by symmetry discussing what message is suggested by the logo image. This has strong links to visual language in the English curriculum. For example, the Canterbury Clothing Company has a logo of three translating, overlapping C’s with a kiwi inside them that give the impression of a single ball moving from left to right.
   
2. Set up a matrix for classifying the logos. Create a chart by pasting logos in the appropriate cell. The Canterbury logo belongs in the bottom right cell as it has no reflective or rotational symmetry. It does have translation symmetry.
   
   The Starbucks logo belongs in the bottom left cell as it has reflective symmetry but no rotational symmetry.

3. Set up the following scenario for the students: 
   You work for an advertising company as a logo designer. There are five new companies that need new logos. They have stipulated that the logo must have some symmetry but must also suggest what goods and services they provide. (If you wish, they may also be required to come up with a slogan that captures the message, e.g. "Just do it".)
   Here are the companies:
   • Sweeties - a company that makes sugar-free lollies that taste great and don’t ruin people’s teeth.
   • Gadgets - who make neat construction gadgets (gears, blocks, wheels, etc.), so people can create their own toys.
   • Mana - an after-school club that supports students in learning te reo Māori.
   • Duds - makers of cool clothes especially for primary school children.
   • Hapori māra - a community organisation that specialises in planting native trees
   • Brainbuilders - the people who provide one-on-one tutoring service for students. You get one-on-one help so you are in a class of your own!
4. Give the students sufficient time to design logos for one or more of the companies. They will need to present the logo in a short report to each company that shows what symmetries are involved and how the design suggests the goods or services the company provides. You may decide to set up a voting system for the class to decide on a winning logo for each company. 

Session Four

1. Provide your students with paper copies of logos (Copymaster 1). Display the logos and ask the students to collaborate (mahi tahi) with a partner and write down the symmetry that each design has (this is useful for assessment purposes). Get pairs to have a korero about what they have written with another pair group, then bring the class together for a collective discussion.
2. For each logo get students to demonstrate what symmetry the design has by using a mirror, or folding and flipping, and by tracing and rotating. Make a list of symmetries for each design.
3. Tell the students to look at their first list and add any information they may have missed. If they do this in a new colour you will have evidence of their initial independent understanding and their new shared understanding.
4. If time permits explore how a simple graphic programme, like PowerPoint, can be used to create simple design elements. By copying the element, reflecting or rotating it, then grouping elements together, complex symmetric design can be created.