Purpose
This is a level 3 algebra activity from the Figure It Out series.
A PDF of the student activity is included.
Student Activity

Click on the image to enlarge it. Click again to close. Download PDF (150 KB)
Specific Learning Outcomes
explore patterns in numbers
Required Resource Materials
FIO, Levels 3-4, Basic Facts, Staircases Capers, page 19
photocopy of the staircases
Activity
In this activity, the students are looking for patterns in numbers. They will need to try several squares, crosses, or staircases before they can be sure that they have found the correct pattern.
Students could use a calculator to speed up their operations, but discourage them from using a calculator for simple operations.
Investigation
As the students investigate different patterns, you could ask the following questions to extend their thinking:
“Will it always work?”
“Would it work on a bigger shape?”
“What other patterns can you make?”
“Can you find out anything about the numbers on diagonal lines?”
“What will happen if you multiply the numbers?”
“What happens for vertical and horizontal lines?”
“Why does it work?”
For example:
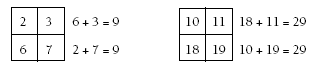
Students may also enjoy investigating patterns of numbers in other situations, for example, in calendar months or hundreds squares. Do the same patterns work?
Here is one pattern that compares 3 x 3 grids on the staircases and on a calendar.
Choose a 3 x 3 set of numbers from one of the staircases. For example:
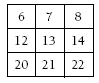
Double the middle number (13 x 2 = 26). Now take any two numbers on the outside of the grid that are directly opposite each other (vertically, horizontally, or diagonally), for example, 7 and 21. Adding them gives 7 + 21 = 28, which is two more than 26. The same is true for 6 and 22, which give 28 when added. Create a new 3 x 3 grid from the staircase and check if the rule holds.
If you do this with a calendar, it gets even more interesting. For example, a grid from the calendar for May 2001 will look like this:
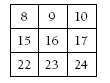
The middle number is 16, and 16 x 2 = 32. Pick a pair of opposite numbers, say 15 and 17. 15 + 17 = 32. Another pair is 10 + 22 = 32.
Use a calendar and check if this rule holds true for any 3 x 3 grid that you pick.
Answers to Activity
1. In each rectangle, pairs of numbers in opposite corners of the rectangle are equal.
2. In each cross, the sum of the two horizontal numbers added is 2 less than the sum of the two vertical numbers added.
3. The sum of the three corner numbers is always 2 more than the sum of the other three numbers in the staircase.
Investigation
Answers will vary and will include different shapes.
For example:
• triangles, such as
• alphabet letters, for example, Z
• multiplying opposite corners
• comparing a 3 x 3 set of numbers on one of the staircases to 3 x 3 grids on a calendar.
Adding and Subtracting Fractions
Identify highest common factors and least common multiples.
Solve problems that involve adding and subtracting fractions.
Number Framework Stage 8
The fact that many students struggle to understand how to add and subtract fractions. The basic notion required is that when fractions have different denominators, they must be renamed to have a common denominator.
Using Number Properties
Problem: “Mele wants to find 1/2 + 1/6. Why can’t the fractions be added directly?” (Answer: Halves and sixths are unlike.)
“How will Mele proceed?”
(Answer: She will convert 1/2 to 3/6, so 1/2 + 1/6 = 3/6 + 1/6 = 4/6.)
Examples: Work out 1/2 – 1/6, 1/8 + 1/2, 7/8 – 1/2, 11/12 – 5/6, 2/3 – 5/12 …
Problem: “Mele wants to work out 8/9 – 5/6 . How will Mele get around the problem of unlike denominators?” (Answer: Mele must find a way to convert both fractions to have a common name.)
List the equivalent names for and on the board.
(Answer: 8/9 = 16/18 = 24/27 = 32/36 = 40/45 = 48/48 ...
5/6 = 10/12 = 15/18 = 20/24 = 25/30 = 30/36 = 35/42 = 40/48 = 45/54 ...)
Discuss which denominators appear in both lists. (Answer: 18, 36, 54 ...)
Discuss why 8/9 = 16/18 and 5/6 = 15/18 are the best fractions to use to rename and 8/9 and 5/6 why 8/9 – 5/6 = 1/18.
Examples : Worksheet (Material Master 8–26).
Understanding Number Properties:
Make up an addition problem for fractions with unlike denominators and then solve it.
Properties of operations
In this unit students work out their own generalisations of the properties of number operations through their exploration of addition, subtraction, multiplication and division.
Patterns are used in the curriculum for several reasons: to develop facility with numbers and calculations, to work on generalisations, and to explore the properties of number operations (which is the focus of this unit). It is important to develop a strong arithmetic basis for interpreting algebraic expressions. This enables students to carry out algebraic manipulations with understanding. For example, the distributive law:
(a + b) x c = a x c + b x c
The distributive law is used constantly in algebraic manipulation, and is a formal statement of a property of addition and multiplication. It states that adding two numbers and then multiplying the answer by 3 (for instance), gives the same answer as if both the numbers were first multiplied by three and then added together. Similarly, students already intuitively know the algebraic equivalence below:
a - (b + 1) = (a - b) – 1
This can be seen in situations such as “if I take 101 away from a number, I get one less than if I take 100 away from it”. At this level, the properties are not expressed with letters, but are illustrated with examples, as the intention is to build up a strong intuition for how the four operations behave.
The questions in this unit are present in algorithm form. However, you should value and build on whatever strategies your students are confident using to add, subtract, divide, and mutiply whole numbers.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
The context for this unit can be adapted to suit the interests and experiences of your students. For example, you might use the context of native animals or native marine life for the problems. Consider how you might make links to a context that is relevant to the learning interests and cultural backgrounds of your students, or to learning from another curriculum area.
Te reo Māori vocabulary terms such as tāpiri (addition), tango (subtraction), whakarea (multiplication), and whakawehe (division) and the te reo Māori words for numbers could be used in this unit and throughout other mathematical learning.
Session 1: Biscuits
Here the students try to find general rules relating to a subtraction problem disguised as a problem involving eating biscuits. Reframe the context of this problem as appropriate.
When you know that 20 – 6 = 14, what other subtractions do you immediately know the answer to?
It might be useful to construct a table of students’ suggestions that may include:
Session 2: Subtraction
In this session, students explore and test properties of subtraction.
Ask a student to come and write a complicated subtraction on the board and work out the answer. For example:
Ask students to suggest other subtractions they can now do easily, using this answer. They might suggest that the top line can be increased (e.g. by 1, 2, 100, 1000, see below), or decreased (e.g. by 30, see below) giving corresponding increases and decreases in the answers. Such examples can be done mentally and checked with a calculator or written algorithm.
Ask the students to suggest other things that we can easily work out using the answer to this subtraction and to explain their reasoning.
Examples: if both numbers are increased by the same amount, the answer is not changed, if both numbers are doubled or halved, the answer would be doubled, if both are multiplied by ten, the answer is multiplied by ten.
Session 3: Multiplication
This session follows the same steps as the above session on subtraction, with a stronger emphasis on checking a variety of numerical examples.
Session 4: Division
This session follows exactly the same steps as the above sessions on subtraction and multiplication.
Session 5: Addition and consolidation
Here the students work by themselves on addition problems. This session is an attempt to bring together the ideas of the previous sessions.
What did you find?
Why did it work?
Will it always work?
Are there any rules that are the same?
Are there any rules that are different?
Dear parents and whānau,
Today in maths we worked out these questions for you to do. See how quickly you can do them. Can you see any patterns?
Take two
This problem solving activity has an algebra focus.
Play the strategy game "take two".
With a partner take turns, removing one or two counters each turn.
The person to remove the last counter is the winner.
Can you find a game strategy so that the first player always win?
Is this a fair game? [In a fair game, each player has an equal chance of winning.]
This is an open problem presented as a game that involves decisions and fairness. Students learn that if it is fair, then it doesn’t matter who starts and each player is equally likely to win. If the game is not fair, then a decision must be made about who will win, the first player or the second player. By playing a number of games students have the opportunity to begin to see a pattern, and to identify a strategy.
The Problem
Play the strategy game "take two".
Place five counters in a row. With a partner take turns, removing one or two counters each turn. The person to remove the last counter is the winner.
Teaching Sequence
What have you noticed in playing this game?
If you are the first player how many counters should you take? Why?
How can you record this pattern?
Extension
Change the number of counters to 7 or any other number you prefer.
Solution
This is an opportunity to work backwards. The person who takes the last counter or the last two counters is the winner (Person A.) Person B, who goes just before this will have had three counters in front of them. (If they had had two, they would have taken away the two and have won. If they had had four, they would have taken away one and left three and so put themselves in the winning position or have taken away two and left two – a losing position.)
So three is a losing position. The next highest losing position is six. This is because if person B sees six counters then B can only take one or two counters away to reduce the pile to five or four. Then person A can take two or one counters to reduce the pile to three and put B in a losing position.
There were five counters originally. The first person who plays is the only one who can get the pile down to three and put the second person in a losing position. So the first player can always win. So the game is not fair.
It’s worth noting that the first player will also win if there are four counters. The first player takes one counter and reduces the pile to three. This is a losing position for the second player.
But six counters in the original pile means a winning game for the second player. No matter what the first player does, the second player reduces the pile to three and wins from there.
In general, if the number of counters originally was a multiple of three, the first person will lose if the second player knows how to play the game. On the other hand if the number of counters is not a multiple of three, then the first player wins by reducing the pile to a multiple of three and making sure that each time they play the pile is reduced to a smaller multiple of three.
We show the first person’s strategy for an 11 counter game in the table below.
Staircase Capers
This is a level 3 algebra activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (150 KB)
explore patterns in numbers
photocopy of the staircases
In this activity, the students are looking for patterns in numbers. They will need to try several squares, crosses, or staircases before they can be sure that they have found the correct pattern.
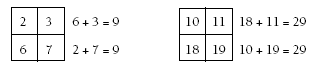

Students could use a calculator to speed up their operations, but discourage them from using a calculator for simple operations.
Investigation
As the students investigate different patterns, you could ask the following questions to extend their thinking:
“Will it always work?”
“Would it work on a bigger shape?”
“What other patterns can you make?”
“Can you find out anything about the numbers on diagonal lines?”
“What will happen if you multiply the numbers?”
“What happens for vertical and horizontal lines?”
“Why does it work?”
For example:
Students may also enjoy investigating patterns of numbers in other situations, for example, in calendar months or hundreds squares. Do the same patterns work?
Here is one pattern that compares 3 x 3 grids on the staircases and on a calendar.
Choose a 3 x 3 set of numbers from one of the staircases. For example:
Double the middle number (13 x 2 = 26). Now take any two numbers on the outside of the grid that are directly opposite each other (vertically, horizontally, or diagonally), for example, 7 and 21. Adding them gives 7 + 21 = 28, which is two more than 26. The same is true for 6 and 22, which give 28 when added. Create a new 3 x 3 grid from the staircase and check if the rule holds.

If you do this with a calendar, it gets even more interesting. For example, a grid from the calendar for May 2001 will look like this:
The middle number is 16, and 16 x 2 = 32. Pick a pair of opposite numbers, say 15 and 17. 15 + 17 = 32. Another pair is 10 + 22 = 32.
Use a calendar and check if this rule holds true for any 3 x 3 grid that you pick.
Answers to Activity
1. In each rectangle, pairs of numbers in opposite corners of the rectangle are equal.
2. In each cross, the sum of the two horizontal numbers added is 2 less than the sum of the two vertical numbers added.
3. The sum of the three corner numbers is always 2 more than the sum of the other three numbers in the staircase.
Investigation
Answers will vary and will include different shapes.
For example:
• triangles, such as
• alphabet letters, for example, Z
• multiplying opposite corners
• comparing a 3 x 3 set of numbers on one of the staircases to 3 x 3 grids on a calendar.
A Close Game
The purpose of this activity is to engage students in using operations on whole numbers to investigate a given context.
This activity assumes the students have experience in the following areas:
The problem is sufficiently open ended to allow the students freedom of choice in their approach. It may be scaffolded with guidance that leads to a solution, and/or the students might be given the opportunity to solve the problem independently.
The example responses at the end of the resource give an indication of the kind of response to expect from students who approach the problem in particular ways.
In the third Bledisloe Cup match between Australia and the All Blacks, in 2014, the game was won by just one point.
The following prompts illustrate how this activity can be structured around the phases of the Mathematics Investigation Cycle.
Make sense
Introduce the problem. Allow students time to read it and discuss in pairs or small groups.
Plan approach
Discuss ideas about how to solve the problem. Emphasise that, in the planning phase, you want students to say how they would solve the problem, not to actually solve it.
Take action
Allow students time to work through their strategy and find a solution to the problem.
Convince yourself and others
Allow students time to check their answers and then either have them pair share with other groups or ask for volunteers to share their solution with the class.
Examples of work
Work sample 1
The student uses chains of addition to find the total number of points for each team. They compare total number of points for each team under the different scoring schemes.
Click on the image to enlarge it. Click again to close.

Work sample 2
The student combines multiplication, addition and subtraction to find the total number of points for each team. They compare total number of points for each team under the different scoring schemes.
Click on the image to enlarge it. Click again to close.

Properties of operations
In this unit students work out their own generalisations of the properties of number operations through their exploration of addition, subtraction, multiplication and division.
Patterns are used in the curriculum for several reasons: to develop facility with numbers and calculations, to work on generalisations, and to explore the properties of number operations (which is the focus of this unit). It is important to develop a strong arithmetic basis for interpreting algebraic expressions. This enables students to carry out algebraic manipulations with understanding. For example, the distributive law:
(a + b) x c = a x c + b x c
The distributive law is used constantly in algebraic manipulation, and is a formal statement of a property of addition and multiplication. It states that adding two numbers and then multiplying the answer by 3 (for instance), gives the same answer as if both the numbers were first multiplied by three and then added together. Similarly, students already intuitively know the algebraic equivalence below:
a - (b + 1) = (a - b) – 1
This can be seen in situations such as “if I take 101 away from a number, I get one less than if I take 100 away from it”. At this level, the properties are not expressed with letters, but are illustrated with examples, as the intention is to build up a strong intuition for how the four operations behave.
The questions in this unit are present in algorithm form. However, you should value and build on whatever strategies your students are confident using to add, subtract, divide, and mutiply whole numbers.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
The context for this unit can be adapted to suit the interests and experiences of your students. For example, you might use the context of native animals or native marine life for the problems. Consider how you might make links to a context that is relevant to the learning interests and cultural backgrounds of your students, or to learning from another curriculum area.
Te reo Māori vocabulary terms such as tāpiri (addition), tango (subtraction), whakarea (multiplication), and whakawehe (division) and the te reo Māori words for numbers could be used in this unit and throughout other mathematical learning.
Session 1: Biscuits
Here the students try to find general rules relating to a subtraction problem disguised as a problem involving eating biscuits. Reframe the context of this problem as appropriate.
When you know that 20 – 6 = 14, what other subtractions do you immediately know the answer to?
It might be useful to construct a table of students’ suggestions that may include:
Session 2: Subtraction
In this session, students explore and test properties of subtraction.
Ask a student to come and write a complicated subtraction on the board and work out the answer. For example:
Ask students to suggest other subtractions they can now do easily, using this answer. They might suggest that the top line can be increased (e.g. by 1, 2, 100, 1000, see below), or decreased (e.g. by 30, see below) giving corresponding increases and decreases in the answers. Such examples can be done mentally and checked with a calculator or written algorithm.
Ask the students to suggest other things that we can easily work out using the answer to this subtraction and to explain their reasoning.
Examples: if both numbers are increased by the same amount, the answer is not changed, if both numbers are doubled or halved, the answer would be doubled, if both are multiplied by ten, the answer is multiplied by ten.
Session 3: Multiplication
This session follows the same steps as the above session on subtraction, with a stronger emphasis on checking a variety of numerical examples.
Session 4: Division
This session follows exactly the same steps as the above sessions on subtraction and multiplication.
Session 5: Addition and consolidation
Here the students work by themselves on addition problems. This session is an attempt to bring together the ideas of the previous sessions.
What did you find?
Why did it work?
Will it always work?
Are there any rules that are the same?
Are there any rules that are different?
Dear parents and whānau,
Today in maths we worked out these questions for you to do. See how quickly you can do them. Can you see any patterns?
The Sieve of Eratosthenes
Solve problems by finding the prime factors of numbers.
Number Framework Stage 8
Eratosthenes, who lived in Greece from about 276 to 195 BC, invented a system to find prime numbers. It consists of crossing out every second number except 2 on a grid then every third number except 3, and so on. The numbers not crossed out are prime. (A discussion about 1 being a special number in that it is neither prime nor non-prime may be worthwhile.)
Using Materials
Give each student a copy of the grid. Notice the number 1 is shaded to indicate it is special. 2 is prime and ringed. Discuss how to cross out all the multiples of 2. (Answer: For example cross out whole columns at a time.)
Ring 3 and cross out all multiples of 3 (that is 6, 9, 12 ... ). Ring 5 and cross out multiples of 5. Continue until all the prime numbers ≤ 200 are ringed.
Discussion: Why is this called a sieve?
Understanding Number Properties:
Describe how you would determine whether 349 is prime using the Sieve of Eratosthenes. Don’t actually do it. Is the method generally useful? Consider for example, testing whether 179 781 is prime.