The first four sessions of this unit are structured around a number of challenges. The cube challenges involve randomly taking one cube from a bag of coloured cubes. To win the challenge you need to take a cube of a particular colour from the bag. Similarly, the spinner challenges involve one spin on a spinner and are won by landing on a particular colour.
For each challenge:
- Introduce the challenge and discuss with ākonga ideas about whether the challenge is fair, and why.
- Have ākonga play the challenge in pairs, recording how many games they play, and how many of these they win (a tuakana/teina model could work well here).
- Discuss how ākonga ideas about whether the challenge is fair have changed now that they have tried it.
- If the challenge is unfair, ask ākonga to suggest how the rules could be changed to make it fair, and then try the challenge with some of the rules suggested.
- Discuss experiences of playing with the changed rules, and whether ākonga think the challenge is now fair.
When discussing whether each challenge is fair, support ākonga to consider the probability of all possible events in a challenge, ordering them from most likely to least likely and identifying events that have the same likelihood of occurring. Ākonga do not need to know the theoretical probabilities involved. However, they should be able to explain their reasoning.
Session one challenges
Cube Challenge I:
Bag contents: one red and one blue multi-link cube
Choose one cube
To win the challenge: take a red cube
This challenge is fair, because there is an equal likelihood of winning (by selecting a red cube) or losing (by selecting a blue cube).
Cube Challenge II:
Bag contents: one red and two blue multi-link cubes
Choose one cube
To win the challenge: take a red cube
This is not a fair challenge because it is more likely that a blue cube will be taken than a red cube. In fact, players are twice as likely to lose the challenge as to win it.
The challenge will be fair if there are an equal number of red cubes and blue cubes. The easiest way to change the challenge so that you win more often, is to add more red cubes. The more red cubes you add, the more likely you are to win the challenge.
Session two
Cube Challenge III:
Bag contents: one red, one blue and one green multi-link cube
Choose one cube
To win the challenge: take a red cube
This is not a fair challenge. There are three equally likely events: take a red, take a blue, or take a green. In terms of the challenge, players are more likely to lose by taking a blue or a green cube, than they are to win by taking a red cube.
The challenge will be fair if there are an equal number of red cubes and cubes that are not red. The easiest way to change the challenge so that you win more often, is to add more red cubes. The more red cubes you add, the more likely you are to win the challenge.
Cube Challenge IV:
Bag contents: three red and two blue multi-link cubes
Choose one cube
To win the challenge: take a red cube.
This is not a fair challenge. There are two events: take a red, or take a blue, and taking a red is more likely than taking a blue. As far as the challenge is concerned players are more likely to win by taking a red (three out of five times) than they are to lose by taking a blue (two out of five times).
The challenge will be fair if there are an equal number of red cubes and cubes that are not red, so the easiest way to change this into a fair challenge is to add one blue cube.
Session three
Spinner Challenge I:
Spinner:
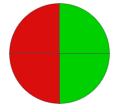
Spin the spinner once
To win the challenge: spinner lands on green
This a fair game as there is an equal likelihood of winning by landing on a green segment, and losing by landing on a red segment.
Spinner Challenge II:
Spinner:
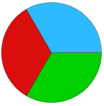
Spin the spinner once
To win the challenge: spinner lands on green
This is not a fair game. There are three equally likely events: land on green, land on red, or land on blue. In terms of the challenge, players are more likely to lose by landing on red or blue, than they are to win by landing on green.
The challenge will be fair if there are an equal number of green segments and segments that are not green. One way to make the challenge fair is to divide the blue segment in half, and colour half of it red, and half of it green.
Session four
Work with Spinner Challenge III and Spinner Challenge IV. For each challenge have ākonga play the game, suggest adaptations to the rules to make the game more fair, and try the new rules out. Discuss their ideas about whether the game is fair and why, throughout.
Spinner Challenge III:
Spinner:
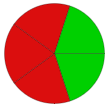
Spin the spinner once.
To win the challenge: spinner lands on green.
This is not a fair challenge. There are two events: land on red, or land on green, and landing on green is less likely than landing on red. As far as the challenge is concerned players are more likely to lose by landing on green (two out of five times) than they are to lose by landing on red (three out of five times).
The challenge will be fair if there are an equal number of green segments and segments that are not green. The easiest way to change this into a fair challenge is to divide one of the red segments in half, and colour half of it green.
Spinner Challenge IV:
Spinner:
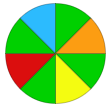
Spin the spinner once.
To win the challenge: spinner lands on green.
This is a fair challenge because there is an equal likelihood of winning (by landing on green) or losing (by landing on a colour other than green).
Session five
- Review a few of the challenges from the week. Discuss the idea of “fairness”. Students might make connections to events that have happened in the playground or during sports games. The key idea to emphasise is that a fair game is a game in which there is an equal chance, or probability, of winning or losing. If the rules of a game change, then the chance of winning or losing (and therefore the fairness of the game) might also change. The picture books Pigs at Odds by Amy Axelrod, It’s Probably Penny by Loreen Leedy, or Bad Luck Brad by Gail Herman could be used to engage students in this discussion.
- Ask ākonga to think about the probability of all possible events in a challenge, ordering them from most likely to least likely and identifying events that have the same likelihood of occurring. Ākonga need not know the theoretical probabilities involved but should be able to explain their reasoning. Words like tōkeke (fair) and tōkeke-kore (unfair) could be introduced here.
- Ask ākonga to work in pairs (a tuakana/teina model could work well here) to make a new challenge using cubes, spinners, or something else that they select. Make specific links to learning from other curriculum areas to support ākonga - the more support they have in an independent task such as this, the more likely they are to succeed. Some ākonga will benefit from working in a small group with the teacher, before going to work independently. Ultimately, ākonga should develop an idea of whether their challenge is fair or not. For extension, ākonga could select fewer or more cubes/segments in their games.
- Have ākonga swap challenges and play them.
- Discuss the challenges faced by ākonga, and have ākonga explain and justify whether or not they think particular challenges are fair.
Robots
In this unit students explore movement and direction concepts in the context of programming a robot to move. They will be developing sets of instructions to accomplish tasks, focusing on the use of right, left, forward, backwards and quarter turns.
At Level 2 the position and orientation element of Geometry builds on work started at Level 1. Students continue to develop the ability to describe position and the direction of movement, and interpret others’ descriptions of position.
The ability to give clear instructions that describe direction and movement clearly is an important skill, which is useful in a wide variety of situations. The context of programming a robot in this unit requires students to think in a logical and systematic way. Finding mistakes, identifying the cause and fixing them will be a feature of the thinking prominent during this unit. This unit also allows skills to be developed that will be useful as students work with computers.
This unit can be differentiated by altering the difficulty of the tasks to make the learning opportunities accessible to a range of learners. For example:
Focus on contexts for giving and following instructions which will appeal to students’ interests and experiences and encourage engagement. Examples may include:
Authentic links could be made to digital technology, and the use of coding programmes. Links could also be made to explanation and procedural writing.
Te reo Māori vocabulary terms such as whakamua (forwards), whakamuri (backwards), mātau (right), maui (left) and kua mutu (end) could be introduced in this unit and used throughout other mathematical learning. Other te reo Māori that could be used for this unit include karehiko (robot) and ngā tohutohu (instuctions).
Getting Started
What is a robot?
What are they used for?
Why are they used?
Can robots think?
Do they have a brain like a human brain?
If not, how do they know what to do?
What sort of instructions do robots need to follow?
What is the name of a person that writes instructions for robots? (programmer)
F means move forward (haere whakamua) one square.
B means move backwards (haere whakamuri) one square.
R means turn to the right (huri whakamatau) 1/4 turn (90°).
L means turn to the left (huri whakamaui) 1/4 turn (90°).
End (kua mutu) means the set of instructions is finished.
If the robot had the cards, F F F F end, what would it do?
What would the instructions, R L R L end, do?
F F F F R F F F F end
What would happen if we changed the L to an R in the set of instructions above?
Where would the robot end up?
Would we end up at the same place if we used the same set of instruction cards but the robot started in a different place?
Where would the robot end up if we started here, but kept the same set of instruction cards?
Starting here, where do you think the robot would end up with this set of instruction cards?
F F F F F B B B B B end
Starting here, where do you think the robot would end up with this set of instruction cards?
Which direction will the robot be facing at the end?
B B B L B B B L B B B L B B B end
Exploring
Over the next 2 or 3 days the students will work in pairs, using the instruction cards to programme the robot to do a series of tasks. The number of tasks and the choice of tasks, need to be worked out by the teacher to ensure all students are challenged and engaged. The tasks do not need to be completed in order, although they do get progressively more difficult going down the page.
The tasks are designed for an 8 x 8 grid with the following headings.
An important part of this unit is developing the students' ability to debug. “Debugging” is the process of finding a mistake, identifying the cause and fixing it. To help students think through the mistake they will make, a counter with an arrow on it to show direction moved over a paper grid may help. Others may need to walk through their instruction cards on the walk-on grid. Working out the set of instructions away from the walk-on grid is important.
Getting the students to place their set of instruction cards onto a ring, a length of string or a pipe cleaner will keep their cards in order when dropped.
Task 1
Start the robot at 7, facing into the grid. Move around the grid and leave at D.
Task 2
Start the robot at 5, facing into the grid. Move around the grid and leave at G. There must be more than one direction cards used, i.e. more than one L or R.
Task 3
Start the robot at F, facing into the grid. Move around the grid and leave at 8. Each type of instruction card, L, R, F, B must be used at least two times.
Task 4
What is the least number of instruction cards needed to start the robot at E, facing into the grid and move around the grid and leave at 6?
Task 5
Start the robot at F, facing into the grid. Move around the grid and leave at 8. Each type of instruction card, L, R, F, B must be used at least two times. For the next two tasks two new instruction cards need to be introduced.
PD means to put down the object the robot is carrying in the square the robot is in. PU means to pick up the object in the square the robot is in. The robot doesn’t move or change directions as it picks up the object.
Task 6
Start the robot at F, facing into the grid. Move around the grid and pick up the object from the diamond and place it at the cross. Leave at F
Task 7
What is the least number of instruction cards needed to start the robot at A, facing into the grid and move around the grid, picking up an object at the star and putting it down at the circle, then leaving the grid at 1?
Task 8
Challenge each other by designing a task for others in your class.
Reflecting
Ask students to think about the things they have learnt this week and discuss. Giving each student a blank piece of paper, ask them to write down one or two important things they have learned, as well as to write down their favourite set of instruction cards. Conclude the week with each team selecting one set of instruction cards, i.e. a completed task, the teacher reads out the instruction task as a student, not the developers, follows the instructions.
Dear family and whānau,
At home this week the homework task is to talk to your family about robots. Find as many situations as you can where robots are used. Think into the future and predict the jobs robots may do in the future or jobs you wish you could programme a robot for.
Number families and relationships
The purpose of this unit of three lessons is to develop an understanding of how the operations of addition and subtraction behave and how they relate to one another.
Algebra is the area of mathematics that uses letters and symbols to represent numbers, points and other objects, as well as the relationships between them. We use these symbols,=, ≠, <, >, and later ≤ and ≥, to express the relationships between amounts themselves, such as 14 = 14, or 14 > 11, and between expressions of amounts that include a number operation, such as 11 + 3 = 14 or 11 + 3 = 16 – 2.
These relationships between the quantities are evident and clearly stated within an equation or expression. This highlights the purpose of an equation or expression, which is to express relationships.
The relationships between the number operations, and the way in which they behave, can be less obvious. Often these operations are part of arithmetic only, as computation is carried out and facts are memorised. However, recognising and understanding the behaviours of, and relationships between, the operations is foundational to success in algebra and arithmetic.
Early on, the relationship between addition and subtraction is explored by connecting the members of a ‘family of facts.’ These ‘fact families’ can be used to facilitate learning of basic facts and to develop a deeper understanding of the relationship between addition and subtraction.
Students often encounter conceptual difficulties in understanding the nature of the operational relationships that exist between three numbers. It is not unusual for students, when asked to write related facts, to write, for example, 3 + 4 = 7, 4 + 3 = 7, 10 – 3 = 7, 10 – 7 = 3. In these statements, equations are correct, but the relationship between 3, 4 and 7 is not understood.
As students encounter more difficult problems, and are required to develop a range of approaches for their solution, having an understanding of the inverse relationship that exists between operations is critical. To ‘just know and understand’ that subtraction ‘undoes’ addition, and that addition ‘undoes’ subtraction becomes very important. For example, it is important to know how and why problems such as 61 – 19 = ☐ can be solved by addition, saying 19 + ☐ = 61, or that the value of n can be found in 12n + 4 = 28, by subtracting 4 from 12n + 4 and from 28. By having a sound understanding of the inverse relationship between addition and subtraction (for example) students are better placed to solve equations by formal means, rather than by simply guessing or following a memorised procedure.
It is important to consider this larger purpose, as we explore ‘families of addition and subtraction facts’. Within this, an equal emphasis must be placed on both operations.
The activities suggested in this series of three lessons can form the basis of independent practice tasks.
Links to the Number Framework
Advanced counting (Stage 4)
Early Additive (Stage 5)
This unit can be differentiated by varying the scaffolding provided or altering the difficulty of the tasks to make the learning opportunities accessible to a range of learners. For example:
Situating the families of facts in familiar additive contexts will appeal to students’ interests and experiences and encourage engagement. Examples may include:
Session 1
SLOs:
Activity 1
Ask students to think of three numbers that they like, between and including 1 and 10. Accept all groups of three numbers, and record them on a class chart.
For example:
1, 2, 3
3, 4, 5
2, 4, 6
4, 7, 10
1, 5, 9
3, 5, 8
Ensure, without pointing this out to the students, that there are some sets that include ‘family of fact’ numbers, For example. eg. 1, 2 ,3, or 3, 5, 8 or 4, 6 10.
Have each pair of students select a set of three numbers for their investigation.
Students take at least four digit cards for each of their chosen numbers, symbol cards, an empty tens frame and counters of two colours.
Pose, “What equations can you make with your numbers? Make a display or record digitally.” (The students with an ‘unrelated’ set of numbers, for example 3, 4, 5 will quickly discover that no equations can be made using all three digits at the same time.)
Discuss their observations, eliciting observations such as, “there are four equations”, “there are two subtraction equations and two addition equations”, “the addition equations are just the other way around (commutative property).”
Activity 2
1, 2, 3
3, 4, 5
2, 4, 6
4, 7, 10
1, 5, 9
3, 5, 8
Ask, “Can you see what we could do to the other groups of numbers to make each of them into a family?” (Change one of the numbers) Accept suggestions and explore ideas.
Take one of these groups, for example 3, 4, 5. Have a student model with counters on a tens frame, 3 + 4. This will show that the third number is 7.
Conclude that 5 can be changed to 7. Explore the other options of changing one of the numbers: 4 to 2, or 3 to 1.
Explore one more example, for example 4, 7, 10. Discuss that instead of 10 this number should be 11. Alternatively, model seven
and highlight the fact that the 4 could be changed to 3. Ask, is there a third thing we could do? (Change 7 to 6).
Have students choose to work in pairs or on their own, to explore the other sets of ‘unrelated numbers’ on the list. They should make a change and write the four equations (+-) which result.
Activity 3
Conclude this session by summarising on the class chart, the features of a family of related facts: three number members of the family, and four equations, two of addition and two of subtraction.
Session 2
SLOs:
Activity 1
(Purpose: To recognise related addition and subtraction equations)
Explain how to play.
Each student has one set of 16 shuffled cards. These are dealt out, face up, in a four-by-four array. Two cards (any) are removed from the array and set aside, creating two empty spaces in the array. Individual cards can be slid across or up and down within the array space, but not lifted, till the array shows one complete ‘family’ in each line or a column. The two cards that were set aside are replaced to complete the array.
To increase the challenge of the task, remove one card only, and/or place each ‘family’ in the same order. (eg. two addition equations then two subtraction equations). Students can swap sets and explore other ‘families’.
Students could write their own sets to create alternative puzzles.
Activity 2
14 + 5 = 19, 5 + 14 = 19, 19 – 14 = 5, 19 – 5 = 14.
Ask students what they notice about what is happening with the numbers.
Record observations such as, “you can add the numbers both ways without changing the result”, “when you subtract you write the biggest number first”, “when you take one of the numbers away you get the other number.”
“Sam helped his Gran with lots of jobs. He earned $5. He helped Grandpa too and he gave Sam $1. Unfortunately Sam lost the $1 on his way home.”
Record, or ask a student to write, the equations that express the scenario on the class chart. (5 + 1 – 1 = 5 and 5 + 1 = 6, 6 – 1 = 5).
Discuss what is happening in these equations. Elicit the observation that subtraction is ‘undoing’ addition.
Record several of these in words and in equations on the class chart.
“Sam had $6 and lost $1 on his way home. He did some extra jobs for his Mum and she gave him $1.”
Record, or ask a student to write, the equations that express the scenario on the class chart. (6 -1 + 1 = 6 and 6 - 1 = 5, 5 + 1 = 6).
Once again, discuss what is happening in these equations. Elicit the observation that addition is ‘undoing’ subtraction.
Explain that we say this relationship between addition and subtraction is known as an inverse relationship. Record this in answer to the question posed in Step 2 above. Have students suggest a meaning for inverse, then confirm this with a dictionary.
Each student could write their own scenario, including a picture or diagram to show what is happening, writing related equations, and an explanation in words of ‘inverse relationship.’
Activity 3
Conclude by sharing and discussing student work.
Session 3
SLOs:
Activity 1
Ask “Why is knowing about families of related facts useful?”
List student suggestions. In particular highlight the commutative property of addition. For example: If you know 17 + 5 = 22, you will also know 5 + 17 = 22. Also highlight the related subtraction facts.
Highlight the importance of the students writing their observations about each grid once they are completed. These observations should include number patterns and the fact that the subtraction grid cannot be fully completed.
For example, 2 + 1 = 3 and 1 + 2 = 3, 2 + 3 = 5 and 3 + 2 = 5.
(Discuss the pattern and also notice the pattern of doubles)
Write this statement on the class chart and read it with the students:
We can carry out addition of two numbers in any order and this does not affect the result. Introduce the word commutative.
Activity 2
Activity 3
(Purpose: to identify three fact family members and to record four related equations.)
The game is played in pairs. The players have one Hundreds Board, 25 counters of one colour each, pencil and paper.
Tens frames showing ten, blank tens frames, and extra counters should be available to the students to model or work out equations if appropriate.
Round one: The Hundreds Board is screened so that numbers 1 – 20 only are visible. Students take turns to place 3 counters on three related numbers. Counters cannot all be placed in the same row.
For example: students cannot cover 3, 4 and 7 because they are all in the same row.
As they place their counters they say and write the four related equations. Students can use tens frames, if needed, to work out or demonstrate the equations and their relationship.
For example:
Player 1
Player 2
Turns continue.
The challenge is to complete the task between them, leaving only two numbers uncovered. If they have more than two uncovered on the first try, they try again with different combinations.
Round two:
The Hundreds Board is screened so that numbers 1 – 30 only are visible. Students take turns to place 3 counters on three related numbers. Counters cannot all be placed in the same row. As they place their counters they say and write the four related equations, using tens frames if needed.
The challenge is to complete the task between them, leaving no more than three numbers uncovered by counters.
Round three:
Numbers 1-50 are made visible. The task is completed. The challenge is to leave just two numbers uncovered by counters.
Dear parents and whānau,
In maths this week, the students have been learning about the relationship between addition and subtraction. They have been exploring fact “families” with three numbers, such as 8 + 6 = 14, 6 + 8 = 14, 14 - 6 = 8 and 14 – 8 = 6. They have found out that subtraction “undoes” addition. (Subtraction is known as the inverse operation of addition, and vice versa).
They have played a game called Family Shuffle. Your child can show you how they have played this. You might like to have a turn, then make up your own fact family together and try the game again.
We hope you enjoy the game, and your discussions, as you make up and talk about new number fact families.
Thank you.
You Don't Need the Number from Book 8: Teaching Number Sense and Algebraic Thinking
How long does it take?
This unit involves students in looking at the lengths of time various activities take and calculating how long is spent on these activities in a week.
Two aspects of mathematics are explored in this unit on time:
This unit can be differentiated by varying the scaffolding provided and altering the difficulty of the tasks to make the learning opportunities accessible to a range of learners to a range of learners. For example:
The contexts in this unit can be adapted to recognise diversity and encourage engagement. For example, ask ākonga to share activities that happen regularly in their families, or activities that they regularly enjoy (for example, going to church, kapa haka practice, sports practice). Adapt the investigations to include these familiar and enjoyable activities.
Te reo Māori vocabulary terms such as wā (time), meneti (minute), and haora (hour) could be introduced in this unit and used throughout other mathematical learning.
Getting Started
How could we work out what seven lots of 2 are all together?
How do you know 5 lots of 5 minutes is 25 minutes altogether?
How could you check?
If we know 2 lots of 5 are ten is it reasonable for 5 lots of 5 to be 8 which is less than that?
How long do you think you would spend brushing your teeth in a week? What did your group find out?
From our calculations which activity takes the most of our time over the course of a week? Which takes the least?
Exploring
How many minutes in an hour? In half an hour?
How did you work out how long she spends each day?
How could you check your calculations?
Is it reasonable to spend that long to brush your teeth? How long do you think it takes you?
Who takes the longest?
How much longer do they take?
How does this compare with how long you would take to do that?
Copymaster 5 can help in these comparisons.
Reflecting
Did you find the statement that was unreasonable? How?
What made you think it was the unreasonable one? How did you check?
Dear parents and whānau,
In maths this week we are focusing on time and on the duration of activities.
This week your child will be timing how long various personal routines take to do. Your assistance and encouragement with the following task is appreciated. You are welcome to add some other activities to the bottom of this table.
Time yourself one day and write down how long it takes to:
Cube and spinner challenges
In this unit we play several games based on coloured cubes and spinners. The purpose is to investigate chance and think about the concept of a fair game.
A fair game is a game in which there is an equal chance of winning or losing. We say that a game is fair when the probability of winning is equal to the probability of losing. Changing the rules of a game can affect the likelihood of winning or losing, and therefore whether the game is fair.
This unit can be differentiated by altering the difficulty of the tasks to make the learning opportunities accessible to a range of learners. For example:
The challenges in this unit can be adapted to recognise diversity and student interests to encourage engagement. For example:
Te reo Māori vocabulary terms such as tōkeke (fair) and tūponotanga (chance) could be introduced in this unit and used throughout other mathematical learning.
The first four sessions of this unit are structured around a number of challenges. The cube challenges involve randomly taking one cube from a bag of coloured cubes. To win the challenge you need to take a cube of a particular colour from the bag. Similarly, the spinner challenges involve one spin on a spinner and are won by landing on a particular colour.
For each challenge:
When discussing whether each challenge is fair, support ākonga to consider the probability of all possible events in a challenge, ordering them from most likely to least likely and identifying events that have the same likelihood of occurring. Ākonga do not need to know the theoretical probabilities involved. However, they should be able to explain their reasoning.
Session one challenges
Cube Challenge I:
Bag contents: one red and one blue multi-link cube
Choose one cube
To win the challenge: take a red cube
This challenge is fair, because there is an equal likelihood of winning (by selecting a red cube) or losing (by selecting a blue cube).
Cube Challenge II:
Bag contents: one red and two blue multi-link cubes
Choose one cube
To win the challenge: take a red cube
This is not a fair challenge because it is more likely that a blue cube will be taken than a red cube. In fact, players are twice as likely to lose the challenge as to win it.
The challenge will be fair if there are an equal number of red cubes and blue cubes. The easiest way to change the challenge so that you win more often, is to add more red cubes. The more red cubes you add, the more likely you are to win the challenge.
Session two
Cube Challenge III:
Bag contents: one red, one blue and one green multi-link cube
Choose one cube
To win the challenge: take a red cube
This is not a fair challenge. There are three equally likely events: take a red, take a blue, or take a green. In terms of the challenge, players are more likely to lose by taking a blue or a green cube, than they are to win by taking a red cube.
The challenge will be fair if there are an equal number of red cubes and cubes that are not red. The easiest way to change the challenge so that you win more often, is to add more red cubes. The more red cubes you add, the more likely you are to win the challenge.
Cube Challenge IV:
Bag contents: three red and two blue multi-link cubes
Choose one cube
To win the challenge: take a red cube.
This is not a fair challenge. There are two events: take a red, or take a blue, and taking a red is more likely than taking a blue. As far as the challenge is concerned players are more likely to win by taking a red (three out of five times) than they are to lose by taking a blue (two out of five times).
The challenge will be fair if there are an equal number of red cubes and cubes that are not red, so the easiest way to change this into a fair challenge is to add one blue cube.
Session three
Spinner Challenge I:
Spinner:

Spin the spinner once
To win the challenge: spinner lands on green
This a fair game as there is an equal likelihood of winning by landing on a green segment, and losing by landing on a red segment.
Spinner Challenge II:
Spinner:

Spin the spinner once
To win the challenge: spinner lands on green
This is not a fair game. There are three equally likely events: land on green, land on red, or land on blue. In terms of the challenge, players are more likely to lose by landing on red or blue, than they are to win by landing on green.
The challenge will be fair if there are an equal number of green segments and segments that are not green. One way to make the challenge fair is to divide the blue segment in half, and colour half of it red, and half of it green.
Session four
Work with Spinner Challenge III and Spinner Challenge IV. For each challenge have ākonga play the game, suggest adaptations to the rules to make the game more fair, and try the new rules out. Discuss their ideas about whether the game is fair and why, throughout.
Spinner Challenge III:
Spinner:

Spin the spinner once.
To win the challenge: spinner lands on green.
This is not a fair challenge. There are two events: land on red, or land on green, and landing on green is less likely than landing on red. As far as the challenge is concerned players are more likely to lose by landing on green (two out of five times) than they are to lose by landing on red (three out of five times).
The challenge will be fair if there are an equal number of green segments and segments that are not green. The easiest way to change this into a fair challenge is to divide one of the red segments in half, and colour half of it green.
Spinner Challenge IV:
Spinner:

Spin the spinner once.
To win the challenge: spinner lands on green.
This is a fair challenge because there is an equal likelihood of winning (by landing on green) or losing (by landing on a colour other than green).
Session five
Dear parents and whānau,
This week we have explored the fairness of different games. The games, or "challenges", we have played involved using coloured cubes and spinners to test out the probability of winning each game. Here is an example.
Cube Challenge: One red and two blue cubes are in a bag. One person chooses one cube. To win the challenge the person must take out a red cube.
This is not a fair 'challenge'. The most likely event is that a blue cube will be taken. Choosing red is less likely. In fact players here are twice as likely to lose the 'challenge' as to win it.
Ask your child to tell you more about the games. It would be good if you and your child could invent and play a 'challenge' of your own. Is it a fair 'challenge'? In other words is it equally likely that you would win or lose this 'challenge'?
Enjoy the challenge!