Purpose
In this unit, students explore the place value system through engaging with a variety of money contexts including trading ($1, $10, and $100 notes) and extended trades and operations into using thousands, millions, and billions of dollars.
Specific Learning Outcomes
- Create groupings of tens, hundreds, thousands, and tens of thousands.
- Read and write large whole number money amounts up to the value of 100 trillion.
- Make sensible estimates for sums that are greater than / less than $10, $100, and $1000.
- Find the sum of collections of $1, $10, $100, $1000, and $10,000 notes.
- Identify different combinations of $1, $10, $100, $1000, and $10,000 that total the same amount.
Description of Mathematics
In this unit students will develop deeper understandings of digits in whole numbers and our place value system within the context of money problems.
Within this, students will explore the fundamentals of our place value system, namely that:
- Our whole number system involves groupings in tens, and trading collections of ten. (Powers of ten are therefore an important concept for learners to develop).
- The same digits are used in different positions to represent different values. (This is often referred to as the distinction between the "face value" of a digit, the "place value" of a digit and the " total value" of a digit. A digit is one of the numerals 0, 1, 2,3, 4, 5, 6, 7, 8, 9)
- Our system is called a base ten place value system. This is reflected in the name decimal where "deci" means based on ten.
- Although there are only ten digits (0 – 9) used in our system, there an endless number of place values that can be assigned to these digits (for example, tens, hundreds, thousands) depending on their position.
- Understanding the role of zero is critical as it serves as an important place holder in our place value system as well as a symbol for ‘nothing of something’.
Opportunities for Adaptation and Differentiation
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- varying the complexity of the numbers that students deal with
- varying the degree of abstraction required by providing or restricting access to materials (Play Money etc.)
- organising groups of students with varying levels of mathematical knowledge and confidence to encourage tuakana-teina (peer learning)
- providing calculators to ease the cognitive load associated with adding large whole numbers
- modelling the use of symbolic recording to ease memory load.
The context of the unit is cash money. Although societal changes may limit students’ experiences with money, the context is still highly motivating. Activities can be adapted to suit the interests and experiences of your students. For example:
- using different place value materials alongside money to help students recognise the proportional relationships not obvious in banknotes and coins
- discussing situations in which large amounts of money are needed, such as fundraising to refurbish a marae, or paying for a trip back to a home country
- sharing everyday situations in which large amounts of money are commonly used (for example, prices of cars, houses, and farms), amounts spent on big events, and money earned annually through private business or enterprises like tourism, forestry, farming, and education
- altering the context for session 5 to focus on how many could be spent on something that is more relevant to your students (e.g. new sports gear, budget for a school camp)
- sharing number vocabulary from other languages, such as Te Reo Māori, as student understanding of number patterns is developed throughout the lessons.
Te reo Māori vocabulary terms such as mehua (measure), rau (hundred), mano (thousand), miriona (million), and monirau (money) could be introduced in this unit and used throughout other mathematical learning.
Required Resource Materials
- Calculators
- A large collection of Play money (Copymaster 1)
- Place Value Houses
- Base 10 / Multi-base / Place value blocks (cubes, longs, flats, large cubes)
- Relevant advertising circulars for sports gear (hard copies or links to digital fliers)
- Plastic bags or envelopes to create pay packets
- Hundred Charts
Activity
Session 1
The following activities are designed for students to work in collaborative groups of 6 –10 students. For the first day, students explore number patterns and relationships that they see in the play money by making amounts with the money and grouping it into ones, tens, hundreds, and other higher place values.
Hand out a mixed bundle of play money with denominations up to $10 000 (from Copymaster 1) to each group of students and have them play "The Great Money Sort!" where they are asked to sort play money into denominations.
The Great Money Sort!
- As students take the mess of play money and begin to sort the money into piles, prompt them to discuss any patterns that they observe. Have students sort as much of the play money as possible. Have them discuss how they are choosing to organise the money into piles, and why.
Possible questions / prompts as students are sorting the money into piles:- What numbers do you see?
- What do you notice about the amounts on these notes (the denominations)?
- Why were these amounts used?
- How is this toy money the same/different to the money we really use?
- The money will get sorted into piles that replicate the place value house designations (ones/tens/hundreds/thousands/ten thousands)
If a greater denomination is needed, what amount should it be? Why? - Discuss how the denominations might be extended to the millions.
Encourage students to offer suggestions about patterns that they see in the numbers and to describe the same pattern in different ways:
What numbers can you see that are the same, or are in the same positions, on all of the notes?
I see the 1 repeating at the start of each denomination (1, 10, 100, 1,000, 10,000…)
I see zeros repeating. (10, 100, 1,000, 10,000…)
I see the zeros growing at the ends of the numbers… 1 zero here – 10 (tens), 2 zeros here - 100 (hundreds), 3 zeros here - 1 000 (thousands) etc.
I see 1, 10, 100 and that keeps repeating in the thousands (1 thousand, 10 thousand, 100 thousand), the millions (1 million, 10 million, 100 million) etc.
Be aware that seeing a symbolic pattern such as “adding zeros” is different from recognising that a given denomination is worth ten times as much as the next smallest denomination, e.g. $100 note is worth ten times $10 note.
Since money is a non-proportional representation of place value you might use a proportional representation as well to help students understand how the quantity changes although the notes all look the same size. Placing matching place value blocks on top of the $1, $10, $100, and $1,000 notes will help.
How big is the block that goes on the …$10,000 note? …$100,000 note? …$1,000,000 note? - Once students have communicated their patterns with the group, turn their attention back to the piles of money. Ask questions that will help students focus on the pattern as grouping by tens (10 ones makes 1 ten, 10 tens makes 1 hundred). This can also be discussed and recorded as powers of ten though this is an interesting pattern, not a requirement at this level (100 = 10 x 10 = 102; 1000 = 10 x 10 x 10 = 103).
Ask questions like:
How many tens do you need to make… one hundred dollars?...one thousand dollars? etc.
How many hundreds do you need to make… one thousand dollars?...ten thousand dollars?etc.
How much do I add… to $380 to make $1,000? To $4,900 to make it $10,000? etc. - Set the groups challenges to find total amounts for various collections of notes. Consider your students’ basic facts knowledge when setting these amounts
Good examples include:
Get 37× $10 notes. How much have you got?
Get 24× $100 notes. How much have you got?
Get 19× $100 notes and 34× $10 notes. How much have you got?
Get 29× $10 notes, 17 $100 notes, and 33× $1 notes. How much have you got?
And other similar questions. - Gather the class to discuss any patterns they noticed. Look for understandings related to place values, such as “If you have 23 × $10 then you multiply 23 by ten to get $230” of “If you have over ten of one note, that will make more of the next biggest note.”
Session 2
Over the next three days, students will continue working with the play money, practise making pay packets in Pay Packet Play, carry out fair trades in the Go Fair Trading Game, explore number problems by grouping money on Place Value Houses, and think about rounding, grouping, and estimating to solve money story problems. Provide students with the opportunity to develop word problems that are relevant to them.
Pay Packets
- For the first day of exploration, provide pairs or small groups of students with plastic bags or clear-faced envelopes into which they can place collections of notes. Discuss a scenario with the students where they control banking and payroll at a company. It is their job to put together worker’s pay packets and keep track of the total amount of money needed to pay staff for the week.
- Provide groups with Copymaster 2 which shows different amounts to be paid to people at the company. Ask students to make up a pay packet for each person and use a calculator or other method to find the total cost of the pay round. Consider whether students would benefit from practice adding whole-numbers, or whether this extra cognitive-load will impede the aim of the lesson (i.e. to read and write large whole-number money amounts).
Roam as students work. Look for:
Can students read the numbers, making use of the groups of digits separated by commas?
Can students recognise the place of digits in the numbers?
Do students understand the significance of zero as indicating none of a denomination?
Do students check to confirm the amount is correct in an organised way? - Rotate the groups so each group checks the pay packets of another group.
Where errors occur, the checking group needs to leave a note explaining the problem. Provide students with time to look back at their original pay packet, rectify any errors, and write a note explaining how they made the error in the first place (if possible). You may need to support students with understanding their errors. - Bring the class together to discuss the task and strategies they employed to get the correct amounts.
The boss is feeling generous as the company has made a good profit this year.
Discuss what the term ‘profit’ means.
She decides to increase each payment by 10% as a bonus.
What does an increase of 10% mean?
Discuss that 10% means 10 in every 100 so each worker will get $10 extra for every $100 they earn.
How much extra will they get for every $1,000 they earn? Every $10 they earn? Every $1 they earn?
Sorry pay clerks, it is your job to include the 10% bonus in every envelope. Get to it. You might get a bonus yourself. - Observe students as they work. Look to see if they develop efficient ways to add 10% to each pay packet. Methods might be cumbersome initially like calculating one tenth of each place value. Support students to realise that multiplying the amount by 10% or 0.1 on a calculator gives the increase. Encourage discussion amongst students as they work through this process and justify their thinking.
- After a suitable time, gather the class to discuss efficient ways to increase each amount by 10%.
How would you increase each payment by 20%? What would that mean?
Students might suggest dividing the amount by ten then adding the answer on to the original amount. You might offer multiplying the amount by 1.1. Why does that work? - Have students challenge each other in groups by one student naming a pay amount, recording the amount as $___ and other students making up the envelope for the employee.
Encourage students to use place value structure rather than counting. Ask questions like:
I put 67× $10 notes in the packet. How much money do you have?
Can you work it out without counting?
I put in 19× $10 000 notes. How much money do you have? How do you know?
I have put in 106× $1 000 notes. How much money do you have? How do you know? - Throughout the pay packet play, have students discuss what patterns they are observing and how they are working out how much is in their pay packet. Students take turns to make pay packets for each other. Have them record their problems using words and numerals on pieces of paper.
Students can discuss possible ways to record the problems using only numerals and symbols.
For example:
10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 = $120 (Repeated addition is less efficient)
or
12 x $10 = $120 (Multiplication is more efficient.) - Finally, vary the pay packet amount through scenarios like working overtime or paying tax. At the conclusion of the lesson, tell students to make up a pay packet with a five-digit dollar amount in it. Encourage students to use a lot of notes, not simply use the digits, such as $12,345 as 1×$10,000 and 2× $1,000, etc. Ask them to record their amount on a pay slip inside the envelope.
Session 3
Go Fair Trading Game
- This activity can be played in a small group or as a whole class. Ask students to sit in a circle. Tell them you are going to give them some money in a pay packet that is theirs to keep and trade with throughout the "Go Fair Trading Game". The aim is to not lose any money as they play each round of the game. Hand out "packets" of pay that were created yesterday. Ask students to check their pay packet of money to see that it matches the pay slip.
- The moves in the Go Fair Trading Game are:
- Find someone else in the group who has an equivalent amount of money made from different denominations with whom they can make a fair trade for their money. For example, one student trades twenty $10 notes with another student in the circle for two $100 notes. These students can make a fair trade as they do not lose any money in the transaction and they both have different denominations of money to make $200.
- Each student must complete five acts of trading and check at the end whether, or not, the packet still contains the correct amount.
Play several rounds, ensuring students receive different pay packets each round. Collect the money at the end of each round.
Encourage students to avoid counting or repeated addition to work out the total of their pay packet. Push them to adopt more efficient strategies such as:
I have thirty $100 notes. I know that ten $100 notes make $1 000 so three groups of ten $100 would be $1 000 + $1 000 + $1 000. That makes 3 x $1 000 or $3 000 altogether that I have.
Also encourage efficient recording strategies, such as a table, with amounts arranged in vertical alignment. This could be completed on paper or on a digital device.
| Note | Number | Total amount |
| $1 | 5 | $5 |
| $10 | 12 | $120 |
| $100 | 34 | $3,400 |
| $1,000 | 6 | $6,000 |
| $10,000 | 17 | $170,000 |
| $100,000 | 9 | $900,000 |
| $1,000,000 | 3 | $3,000,000 |
| Sum | | $4,079,525 |
Continue discussing the trades increasing the complexity and number size with each round. Have students share and record their strategies for each round.
- Provide a challenging problem to complete the lesson:
[Name] has $27,094 in his/her pay packet.
How many notes are in his/her pay packet?
How many different answers can you find?
Encourage the students to think beyond the simplest answer of 2 + 7 + 9 + 4 = 22 notes.
Session 4
Place Value Houses and Problems
In this lesson students make further links between the play money and the place value system by placing money on the Place Value Houses template. Students will gain confidence reading multi-digit whole numbers using the Place Value Houses to help them to structure large whole numbers. They will solve addition and subtraction problems by using their knowledge of grouping play money in tens/hundreds/thousands/ten thousands. and by making sensible estimates that they can check with the play money.
- Use A3 laminated Place Value Houses (Material Master 4-11) along with the Play Money that has been used throughout the past lessons. Ask students to explain the structure of the Place Value Houses template.
- Students should connect the Place Value Houses in order starting with the "Trend setter house" on the far right. These three columns refer to the ones period. Each set of three places is a period. Next left from ones, is the thousands period, then the millions period, etc. It is helpful to record $1, $1,000, $1,000,000, $1,000,000 so students understand how commas are used to separate periods when money amounts are written. That system makes reading large numbers easier than a string of digits. Note the use of gaps and commas in writing. large numbers. Display both conventions to your class and choose one to use throughout this unit.
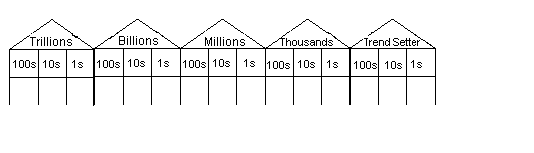
- Ask students to read the amount $111,111,111 and make that amount using play money on the Place Value Houses template. Ask them to remove notes and read the resulting amount, e.g. $101,111,111.
- Have pairs or trios of students place all their play money into piles in the appropriate places in the House template, e.g. $100 notes in the hundreds place.
- Tell students to remove most notes from each column, so there are just a few notes in each place. Ask them to work out how to read and write the amount they have left. Students can swap their amounts with a neighbouring pair or trio for more practice.
- On the whiteboard or on a piece of paper, write amounts of money. Ask students to read then make the amounts, such as:
$3,450
$75,010
$407,908
$37,090,324 - Let students challenge another pair or small group to tell them what piles of money they would place on the Place Value Houses for an amount that they write on paper. Practise reading the amounts as well.
- Help students read increasingly large numbers by always having them begin reading numbers at the far left and saying first the "ones, tens and hundreds" and then the Place Value House name and so on.
In this way, the number $45 874 230 would be explained and read as:
(Always start reading with the far-left-hand side of the number):
(ones, tens, hundreds) 45 (millions house) million, (ones, tens, hundreds) 874 (thousands house) thousand, (ones, tens, hundreds) 230 (trend setter house so we just say the number of ones, tens, hundreds). - Practise reading each other’s large numbers written on paper and making them on the Place Value Houses.
Session 5
For the final day, students will be given an open-ended task involving Advertising circulars (such as a Warehouse, Rebel Sport or Farmers advertising flyer) and play money.
- The teacher should discuss the learning task with students and then roam and observe the strategies used by students. Students can use the play money, Place Value Houses, number lines and hundred charts to assist them as they work and reflect on the following task.
- Open-Ended Task: This is the class's lucky day! We have received an envelope from a mysterious donor with ten $100 notes inside! Your task:
- Work out how much money you have. The aim is to spend as much of that amount as you can without going into debt.
- Look through the advertising flyers provided and decide on the items you would really like to purchase for our classroom, other classes around the school, what you’d like to donate, and what you’d like to save.
- See if you can combine 2 or more items that you would like to buy and estimate if you will have enough money to buy them.
- Try to work out the maximum number of items that you can buy with your money.
- Record your preferred purchases on paper.
- Be prepared to discuss how you have worked out the amounts.
- You may use play money, place value houses and any of the number lines or charts to help you.
Home Link
Dear family and whānau,
At school this week we have been practising counting play money by looking for patterns with ones, tens and hundreds that relate to our place value system.
Weekly Budget and Shopping Planning!
I would like your child to help you plan for the weekly shopping by finding out how much money they have to budget for some food purchases this week. They can then look through food store advertising flyers or online to spot the best deals on some basic food items. Have them work on a list of 5-10 food items to be purchased for the week keeping in mind an amount of money they would have to spend. Students can estimate the cost of items by rounding food item costs to the nearest $1, $5, $10.
For example, if the family wants to purchase two boxes of cereal and each box costs $4.99 they can round each box to $5. Two boxes at $5 each makes $10 towards cereal for the week.
Item to be purchased | Number of items needed | Cost of each item | Total estimate | Total cost of the items |
| cereal | 2 boxes | $4.99 | 2 x $5 | $10 |
| bread | 5 loaves | $1.89 | 5 x $2 | $10 |
| milk | 2 litres | $3.99 | $5 | $5 |
| | | | | $25 |
Fraction Benchmarks
In this unit students develop important reference points or benchmarks for zero, one half and one. They use these benchmarks to help compare the relative sizes of fractions, through estimating, ordering and placing fractions on a number line.
This unit builds on the following key conceptual understandings about fractional parts.
An understanding of fractional parts supports students to develop a sense for the size of fractions. This unit helps students develop an intuitive feel for zero, one-half and one, as useful benchmarks for ordering fractions. Understanding why a fraction is close to zero, one half or one helps students develop a number sense for fractions.
Students can be supported through the learning opportunities in this unit by differentiating the complexity of the tasks, and by adapting the contexts. Ways to support students include:
The contexts for this unit are purely mathematical but can be adapted to suit the interests and cultural backgrounds of your students. Fractions can be applied to a wide variety of problem contexts, including making and sharing food, constructing items, travelling distances, working with money, and sharing earnings. The concept of equal shares and measures is common in collaborative settings. Students might also appreciate challenges introduced through competitive games or through stories.
Session 1
In this session students begin to develop benchmarks for zero, half and one.
1/20, 6/10, 10/8, 11/12, 1/10, 3/8, 2/5, 9/10.
As the difficulty of this task depends on the fractions, begin with fractions that are clearly close to zero, half or one.
Why do you think 6/10 is close to half? How much more than a half is it? Why do you think 1/20 is close to zero? How much more than zero? Why is 11/12 close to one? Is it more or less than one? How much less?
3/10, 5/6, 5/9, 4/9, 18/20, 13/20, 2/8, 9/12, 1/5
Once more encourage the students to explain their decision for each fraction.
Session 2
In this session the students continue to develop their sense of the size of fractions in relation to the benchmarks of zero, half and one by coming up with fractions rather than sorting them.
5/6
How do you know that fraction is close to one?
5/6 7/8
How do you know that 7/8 is closer to one than 5/6?
Students might comment on how much needs to be added to each fraction to make it equal to one. "7/8 is closer to one because eighths are smaller parts than sixths and 7/8 is 1/8 smaller than 1 and 5/6 is 1/6 smaller than one. As 1/8 is smaller than 1/6, 7/8 is closer to one."
Do you notice a pattern as the fraction gets closer to one? (5/6, 7/8, 9/10, 11/12)
Which fraction is closer to one 99/100 or 999/1000? Why?
Which of these fractions is closest to zero, 1/3, 1/4, 1/5, or 1/6? Explain why?
Can a fraction have 5 as a numerator but still be close to zero? Give an example.
Session 3
In this session students estimate the size of fractions.
Ask for volunteers to record their estimate on the board. As they record estimates, ask each student to share their reasoning. Listen, without judgement to the estimate and then discuss why any given estimate might be a good one. Encourage students to share their justifications and ask questions of each other. There is no single correct answer but the estimates need to be reasonable. If the students are having difficulty, encourage them to reflect on the benchmarks developed in the previous sessions. Look for creative methods like estimating that the white area combines to 1/4 so the shaded area must be 3/4
Session 4
In this activity students identify which fraction of a pair is larger. The comparisons rely on an understanding of the top and bottom number (numerator and denominator) in fractions and on the relative sizes of the fractional parts. Equivalent fractions are not directly introduced in this unit but if they are mentioned by students they should be discussed.
2/5 or 2/8
Encourage explanations that show that the students understand that the fractions have the same number of parts but that the parts are different sizes. In this example 2/8 is smaller than 2/5 because eighths are smaller than fifths. Some students may know that 2/8 = 1/4. Use Fraction Strips to check students predictions.
4/5 or 4/6.
Encourage explanations that show that the students understand that both these fractions have the same count (numerator) but fifths are larger than sixths. Therefore 4/5 is greater than 4/6. Write 4/5 > 4/6. Use Fraction Strips to check students' predictions.
In this example the students can draw on their understanding of the benchmark of 1 and notice that 10/9 is larger than 1 and 9/10 is smaller than 1.
7/10 or 6/10
6/8 or 6/12
3/8 or 4/10 (more difficult)
9/8 or 4/3 etc
One fraction is greater than the other.
The two fractions have different numerators and different denominators.
What might the fractions be?
Session 5
In this session the students draw on their conceptual understanding of fraction benchmarks (0, 1/2, 1) and their understanding of the relative sizes of fractional parts to line fractions up on a number line.
Dear family and whānau,
This week we are learning about where fractions live on number lines. We have been especially interested in fractions that are close to zero, close to one half and close to one. Ask your child to put the following fractions on a number line and explain to you how they made up their mind about where to place them.
1/30 2/99 44/85 99/100 25/60 3/25 77/80 26/50
Fraction circles
These exercises and activities are for students to use independently of the teacher to practice number properties.
Prior knowledge.
Students should have completed the activity ‘fair shares’ Book 7, Fair Shares
Background
Ordering unit fractions and non-unit fractions, without using equipment involves quite different skills, and are found at different stages of the knowledge framework. A useful introduction to sorting non-unit fractions is to develop students’ strategies for identifying when a fraction is close to one (eg is close to one as there is only 1 little piece missing from a whole) or zero. Likewise for fractions below or above one half (for example 2/5 is less than one half as in one half, the denominator is double the numerator. In two fifths, doubling 2 gives a number smaller than the denominator).
Comment on the Exercises
Exercise 1
Asks students to identify the bigger fractions in a pair.
Exercise 2
Asks students to order 3 unit fractions from smallest to biggest.
Exercise 3
Asks students to identify the bigger fraction in a pair. Fractions are halves, quarters, thirds, and fifths.
Exercise 4
Asks students to order 3 fractiosn from biggest to smallest. The fractions are halves, quarters, thirds, and fifths.
Exercise 5
Asks students to solve word problems that involve identifying the largest fraction.
These activities can be used to follow the teaching episodes based on, Book 7, Fraction Circles and are for those students who are able to use the associated number properties.
Paper-folding Fractions
This activities is for students to use independently of the teacher to practice number properties
find fractions using paper folding
Number Sequence and Order, AA (Stage 6)
Paper Folding Fractions 1 (PDF or Word)
Student Project (PDF or Word)
Prior knowledge.
Background
To become effective users of multiplication and division, students need to develop an understanding of the role of factors in these operations. For example, multiplying by two then five is the same as multiplying by ten, dividing by four is the same as dividing by two then two again. The relationship between division and fractions is also an important one to identify. This practical activity helps students to start exploring such relationships.
This activity also encourages students to consider how to create quality work – what is most important and what is less important. It also gives them practice at looking at work, providing constructive feedback and looking at how to improve work.
Comments on the Exercises
Exercise 1
Asks students to explore related fractions of 1/2, 1/4, 1/8s using paper folding.
Exercise 2
Asks students to explore related fractions of 1/3s and of 1/5s using paper folding.
Student Project
Asks students to work in groups to produce a poster about the mathematics they learnt in the paper folding fractions.
These activities can be used to follow the teaching episodes based on paper folding fractions 1 and 2, which are also listed under teaching activities. This activity is for those students who are able to use the associated number properties.
Rounding: closest to
This exercise is for students to use independently of the teacher to practice number properties.
round to the nearest ten or hundred
use the sign that means “approximately equals”
Grouping/place value, EA (Stage 5)
Prior knowledge.
Identify when a number is “closer to”
Background
This activity is an introductory exercise designed to introduce students to the idea of approximate numbers and rounding. It is knowledge based. This exercise is about rounding numbers to the nearest 10 or 100and introduces students to talking about the approximate size of numbers. In doing this it also introduces them to a new symbol (≈ or the ‘squiggly equals’). Teachers need to be aware that this symbol needs to be used in the context of a problem, with the questions in this exercise being a very simple class of these.
Rounding numbers can only be sensibly done in a context. 672 can be correctly rounded to 670 adn also to 700, the context of the problem determines whichis more sensible. If taken out of the context of the problem, and the numbers in that problem, its use can lead to some nonsensical statements. For example, saying that 150 is approximately 200, or pi (3.1415928…) is close to zero is not very helpful mathematically. However in the context of the problem 47 ÷ 123,456,789 saying that 47 ≈ 0, so the answer is approximately zero does make sense
Comments on the Exercise
Money Matters
In this unit, students explore the place value system through engaging with a variety of money contexts including trading ($1, $10, and $100 notes) and extended trades and operations into using thousands, millions, and billions of dollars.
In this unit students will develop deeper understandings of digits in whole numbers and our place value system within the context of money problems.
Within this, students will explore the fundamentals of our place value system, namely that:
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
The context of the unit is cash money. Although societal changes may limit students’ experiences with money, the context is still highly motivating. Activities can be adapted to suit the interests and experiences of your students. For example:
Te reo Māori vocabulary terms such as mehua (measure), rau (hundred), mano (thousand), miriona (million), and monirau (money) could be introduced in this unit and used throughout other mathematical learning.
Session 1
The following activities are designed for students to work in collaborative groups of 6 –10 students. For the first day, students explore number patterns and relationships that they see in the play money by making amounts with the money and grouping it into ones, tens, hundreds, and other higher place values.
Hand out a mixed bundle of play money with denominations up to $10 000 (from Copymaster 1) to each group of students and have them play "The Great Money Sort!" where they are asked to sort play money into denominations.
The Great Money Sort!
Possible questions / prompts as students are sorting the money into piles:
If a greater denomination is needed, what amount should it be? Why?
Encourage students to offer suggestions about patterns that they see in the numbers and to describe the same pattern in different ways:
What numbers can you see that are the same, or are in the same positions, on all of the notes?
I see the 1 repeating at the start of each denomination (1, 10, 100, 1,000, 10,000…)
I see zeros repeating. (10, 100, 1,000, 10,000…)
I see the zeros growing at the ends of the numbers… 1 zero here – 10 (tens), 2 zeros here - 100 (hundreds), 3 zeros here - 1 000 (thousands) etc.
I see 1, 10, 100 and that keeps repeating in the thousands (1 thousand, 10 thousand, 100 thousand), the millions (1 million, 10 million, 100 million) etc.
Be aware that seeing a symbolic pattern such as “adding zeros” is different from recognising that a given denomination is worth ten times as much as the next smallest denomination, e.g. $100 note is worth ten times $10 note.
Since money is a non-proportional representation of place value you might use a proportional representation as well to help students understand how the quantity changes although the notes all look the same size. Placing matching place value blocks on top of the $1, $10, $100, and $1,000 notes will help.
How big is the block that goes on the …$10,000 note? …$100,000 note? …$1,000,000 note?
Ask questions like:
How many tens do you need to make… one hundred dollars?...one thousand dollars? etc.
How many hundreds do you need to make… one thousand dollars?...ten thousand dollars?etc.
How much do I add… to $380 to make $1,000? To $4,900 to make it $10,000? etc.
Good examples include:
Get 37× $10 notes. How much have you got?
Get 24× $100 notes. How much have you got?
Get 19× $100 notes and 34× $10 notes. How much have you got?
Get 29× $10 notes, 17 $100 notes, and 33× $1 notes. How much have you got?
And other similar questions.
Session 2
Over the next three days, students will continue working with the play money, practise making pay packets in Pay Packet Play, carry out fair trades in the Go Fair Trading Game, explore number problems by grouping money on Place Value Houses, and think about rounding, grouping, and estimating to solve money story problems. Provide students with the opportunity to develop word problems that are relevant to them.
Pay Packets
Roam as students work. Look for:
Can students read the numbers, making use of the groups of digits separated by commas?
Can students recognise the place of digits in the numbers?
Do students understand the significance of zero as indicating none of a denomination?
Do students check to confirm the amount is correct in an organised way?
Where errors occur, the checking group needs to leave a note explaining the problem. Provide students with time to look back at their original pay packet, rectify any errors, and write a note explaining how they made the error in the first place (if possible). You may need to support students with understanding their errors.
The boss is feeling generous as the company has made a good profit this year.
Discuss what the term ‘profit’ means.
She decides to increase each payment by 10% as a bonus.
What does an increase of 10% mean?
Discuss that 10% means 10 in every 100 so each worker will get $10 extra for every $100 they earn.
How much extra will they get for every $1,000 they earn? Every $10 they earn? Every $1 they earn?
Sorry pay clerks, it is your job to include the 10% bonus in every envelope. Get to it. You might get a bonus yourself.
How would you increase each payment by 20%? What would that mean?
Students might suggest dividing the amount by ten then adding the answer on to the original amount. You might offer multiplying the amount by 1.1. Why does that work?
Encourage students to use place value structure rather than counting. Ask questions like:
I put 67× $10 notes in the packet. How much money do you have?
Can you work it out without counting?
I put in 19× $10 000 notes. How much money do you have? How do you know?
I have put in 106× $1 000 notes. How much money do you have? How do you know?
Students can discuss possible ways to record the problems using only numerals and symbols.
For example:
10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 = $120 (Repeated addition is less efficient)
or
12 x $10 = $120 (Multiplication is more efficient.)
Session 3
Go Fair Trading Game
Play several rounds, ensuring students receive different pay packets each round. Collect the money at the end of each round.
Encourage students to avoid counting or repeated addition to work out the total of their pay packet. Push them to adopt more efficient strategies such as:
I have thirty $100 notes. I know that ten $100 notes make $1 000 so three groups of ten $100 would be $1 000 + $1 000 + $1 000. That makes 3 x $1 000 or $3 000 altogether that I have.
Also encourage efficient recording strategies, such as a table, with amounts arranged in vertical alignment. This could be completed on paper or on a digital device.
Continue discussing the trades increasing the complexity and number size with each round. Have students share and record their strategies for each round.
[Name] has $27,094 in his/her pay packet.
How many notes are in his/her pay packet?
How many different answers can you find?
Encourage the students to think beyond the simplest answer of 2 + 7 + 9 + 4 = 22 notes.
Session 4
Place Value Houses and Problems
In this lesson students make further links between the play money and the place value system by placing money on the Place Value Houses template. Students will gain confidence reading multi-digit whole numbers using the Place Value Houses to help them to structure large whole numbers. They will solve addition and subtraction problems by using their knowledge of grouping play money in tens/hundreds/thousands/ten thousands. and by making sensible estimates that they can check with the play money.
$3,450
$75,010
$407,908
$37,090,324
In this way, the number $45 874 230 would be explained and read as:
(Always start reading with the far-left-hand side of the number):
(ones, tens, hundreds) 45 (millions house) million, (ones, tens, hundreds) 874 (thousands house) thousand, (ones, tens, hundreds) 230 (trend setter house so we just say the number of ones, tens, hundreds).
Session 5
For the final day, students will be given an open-ended task involving Advertising circulars (such as a Warehouse, Rebel Sport or Farmers advertising flyer) and play money.
Dear family and whānau,
At school this week we have been practising counting play money by looking for patterns with ones, tens and hundreds that relate to our place value system.
Weekly Budget and Shopping Planning!
I would like your child to help you plan for the weekly shopping by finding out how much money they have to budget for some food purchases this week. They can then look through food store advertising flyers or online to spot the best deals on some basic food items. Have them work on a list of 5-10 food items to be purchased for the week keeping in mind an amount of money they would have to spend. Students can estimate the cost of items by rounding food item costs to the nearest $1, $5, $10.
For example, if the family wants to purchase two boxes of cereal and each box costs $4.99 they can round each box to $5. Two boxes at $5 each makes $10 towards cereal for the week.
Item to be purchased
Number of items needed
Cost of each item
Total estimate
Total cost of the items
Figure it Out Links
Some links from the Figure It Out series which you may find useful are:
The following books contain activities to help students investigate and evaluate financial decisions. Some of these involve operating with number.
Cards to 24
In this activity students use a deck of cards (or create their own set of cards with numbers on) to play a version of the 24 game. Students will use four cards and combinations of the four arithmetic operations to try to make a total of 24.
use the four arithmetic operations to make number sentences, which total 24.
5 – 3 = 2
2 x 9 = 18
18 + 6 = 24
(It should be noted that not all sets of four cards will have a possible solution.)
Tennis Ball Multiplication
The purpose of this activity is for students to practice their multiplication basic facts
recall the multiplication basic facts.
Roughly how many?
In this activity we look at cubes which have been roughly sorted into arrays and decide about how many there are. We use our knowledge of multiplication facts to estimate the number of cubes.
use arrays to solve estimation problems
Overhead projector (if available)
Did you see more than 20 cubes? Why do you think that?
Did you see more than 20 cubes? Why do you think that?