Getting started

Starting with a simple pattern, we build up the level of difficulty and see that it’s necessary to use a table to record what is happening.

1. Build up the letter ‘I’ using coloured tiles or paper (see the diagram below).
   How many tiles do we need for the first ‘I’? The second? The third?
   

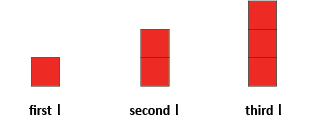
   Who can tell me how many tiles we’ll need for the fourth ‘I’?
   Can someone come and show us how to make the fifth ‘I’?
   How many tiles will we need for the tenth ‘I’? Make it.
   What is the number pattern that we are getting?
   If we had 11 tiles, which numbered ‘I’ could we make?

2. Now let’s make it a bit harder. Let’s make an ‘I’ by adding a tile to the top and the bottom each time (see diagram).

   Repeat the questions from the last ‘I’ problem.
   How many tiles do we need for the first ‘I’? The second? The third?
   Who can tell me how many tiles we’ll need for the fourth ‘I’?
   Can someone come and show us how to make the fifth ‘I’?
   How many tiles will we need for the tenth ‘I’? Make it.
   What is the number pattern that we are getting?
   How many tiles do we add on at each step?
   If we had 11 tiles, which numbered ‘I’ could we make?

3. It was easy to see what was happening in the original ‘I’ problem and to see how many tiles each ‘I’ needed. It wasn’t quite as easy with the second one we did. But what if we had a really difficult pattern? How could we keep track of what’s going on and see how many tiles we need for each letter (reta)?
   After korero, suggest the idea of a table.

4. The original ‘I’ problem would give us an easy table. It would look like this:

   ‘I’ number	1	2	3	4	5
   Number of tiles	1	2	3	4	5

   What would the table look like where we added two tiles at a time?
   Draw up the table with help from the ākonga

5. Now let the ākonga complete the table for the letter pattern on Copymaster 1. Support ākonga the while they are working and help them by asking leading questions such as:
   How did you know how many tiles to use on the fourth ‘L’?
   What is the pattern (tauira) here?
   Which ‘L’ in the sequence will use 27 tiles?
6. Bring the class back together and discuss their work.
   Tell me what numbers you used to fill the table. (Check that they are correct by counting the tiles.)
   What patterns can you see here?
   How did you get the number of tiles for one ‘L’ from the one before?
   How many tiles would you need for the 10th ‘L’?
   If you had 23 tiles, what numbered ‘L’ could you make?

Exploring

For the next three days the ākonga work at three stations continuing different number patterns and building up the corresponding tables. In the first station, the ākonga complete a similar problem to the one in ‘Getting Started’. In the second station the ākonga find a missing shape in the pattern sequence. Finally in the third station ākonga make their own pattern that fits the given table of values.  Ākonga could work in three groups that provide tuakana/teina support. At the end of each day, bring them back together to discuss their thinking. Ask them the kind of questions that were used in ‘Getting Started’. Use the tables to discuss the patterns involved and the relation between successive numbers in the sequence.

Day 1
The material for these stations is on Copymasters 1.1, 1.2, 1.3, 1.4. The ākonga continue the pattern and complete the table. Ākonga could continue to use tiles to support their learning.

Day 2
The material for these stations is on Copymasters 2.1, 2.2, 2.3, 2.4. The ākonga find the missing element of the pattern and complete the table. Tiles could be provided for some ākonga who may need to construct the missing element before drawing it.

Day 3
The material for these stations is on Copymasters 3.1, 3.2, 3.3, 3.4. The ākonga make up their own pattern to fit the values in the table. Ākonga could use the tiles to create patterns and count to check that they match the numbers in the table before drawing them on the sheet. 

Reflecting

On the final day let the ākonga make up their own patterns using numbers or shapes, instead of letters. They could construct these with tiles first, or by drawing. Encourage ākonga to think of patterns in their environment, for example, tukutuku patterns in the local wharenui or museum. Ākonga should also provide a table to show the number pattern of their number or shape.  Some ākonga might want to leave gaps in the patterns of their numbers or shapes. Other ākonga could fill this in when they share their pattern with the class.

When ākonga are sharing their patterns with the class, point out the importance of the table in seeing what the number pattern is.

Getting Started

Today we look at the number patterns in a tower of tins (tini).

1. Tell the students that today we will stack tins for a supermarket (hokomaha) display.

2. Show the students the arrangement:

   

   How many tins are in this arrangement?
   How many tins will be in the next row (kapa)?
   Then how many tins will there be altogether?
   How did you work that out?

3. Encourage the students to share the strategy they used to work out the number of tins. “I can see 4 tins and know that you need 5 more on the bottom. 4 + 5 = 9”

   “I know that 1 + 3 + 5 = 9 because 5+3= 8 and 1 more is 9.”
   [These strategies illustrate the student’s knowledge of basic addition facts.]

4. Show the students the next arrangement of tins. They can check that their predictions were correct.

   

   How many tins will be in the next row? 
   Then how many tins will there be altogether?
   How did you work that out?

5. Encourage the students to share the strategies they used to work out the number of tins.
   “I know that we need to add 7 to 9 which is 16.” [knowledge of basic facts]
   “I know that 7+ 9 = 16 because 7 + 10 = 17 and this is one less." [early part-whole reasoning]
   “I know that we are adding on odd numbers each time. 1+3+5+7 = 16 because 7+3 is 10 + 5 + 1 = 16."

6. Add seven tins to the arrangement and ask the same questions. As the numbers are becoming larger expect the range of strategies used to be more varied.

   

   “16 + 9 = 25. I counted on from 16.” [advanced counting strategy]
   “16 + 10 = 26 so it is one less which is 25.” [part-whole strategy]

7. Tell the students that the supermarket has asked for the display to be 10 rows high.
   How many tins will you need altogether?
8. Ask the students to work in small groups to find out how many tins are needed. As the students work circulate asking:
   How are you keeping track of the numbers?
   Do you know how many tins will be on the bottom row? How do you know?
9. Gather the students back together as a class to share solutions.
10. Discuss the methods that the groups have used to keep track of the number of tins.
11. Work with students to make a table showing the number of rows and total number of tins. Complete the first couple of rows together.
12. Ask the small groups to complete their own copy of the table on Copymaster 1. As they complete the chart ask:
    Can you spot any patterns?
    Write down what you notice?
    Can you predict how many tins would be needed when there are 15 in the bottom row?
13. Encourage the students to explain their strategies for “counting” the numbers of tins.
14. As a class, share the patterns noted.

Exploring

Over the next 2-3 sessions the students work with a partner to investigate the patterns in other stacking problems. Consider pairing together students with mixed mathematical abilities (tuakana/teina). We suggest the following introduction to each problem.

1. Pose the problem to the class and ask the students to think about how they might solve it. In particular encourage them to think about the table of values that they would construct to keep track of the numbers.
2. Share tables.
3. Ask the students to work with their partner to construct and complete their own table.

4. Write the following questions on the board for the students to consider as they solve the problem.

   How many tins are in the first row? 
   How many are in the second row?
   By how much is the number of tins changing as the rows increase?
   What patterns do you notice?
   Can you predict how many tins would be needed for the bottom row if the stack was 15 rows high?
   Explain the strategy you are using to count the tins to your partner?
   Did you use the same strategy?
   Which strategy do you find the easiest?

5. As the students complete the tables and solve the problem, circulate and ask them to explain the strategies that they are using to “count” the numbers of tins in the design.
6. Share solutions as a class.

Problem 1:

Copymaster 1

A supermarket assistant was asked to make a display of sauce tins. The display has to be 10 rows high.
How many tins are needed altogether?
What patterns do you notice?

Problem 2:

Copymaster 2

A supermarket assistant was asked to make a display of sauce tins. The display has to be 10 rows high.
How many tins are needed altogether?
What patterns do you notice?

Problem 3:

Copymaster 3

A food demonstrator likes her products displayed using a cross pattern. The display has to be 10 products wide.
How many products are needed altogether?
What patterns do you notice?

Reflecting

In this session the students create their own “growth” pattern for others to solve.

1. Display the growth patterns investigated over the previous sessions.
2. Gather the students as a class and tell them that their task for the day is to invent a pattern for the supermarket to use to display objects.
3. Ask the students in small groups to decide on a pattern and the way that it will grow. (A supply of counters may be helpful for some students.)
4. Direct students to construct a table to keep track of their pattern (up to the 10^th model). Model how to construct and use this. Alternatively, you could provide a graphic organiser for students to use.
5. Once they have constructed the table ask them to record the any patterns that they spot in the numbers. Ask them also to make predictions about the 15^th and 20^th model. 
6. Direct students to swap problems with another group. When the problem has been solved, they should compare solutions with each other.

Note: All of the patterns used in this unit are available in PowerPoint 1 to allow easy sharing with Smart TV or similar.

Session 1: Triangle Paths

In this session we look at a simple pattern created by putting matches together to form a connected path of triangles.

1. Introduce the session by telling the students that Kiri made the following matchstick paths using 1, 2, and 3 triangles – she called them a 1-triangle path, a 2-triangle path, and a 3-triangle path. Note that 1, 2, and 3 are the term numbers in Kiri’s pattern.
   
2. Ask the students to use Kiri’s method to make a 4- and then a 5-triangle path.
   How many extra matches would be needed to make a 6-triangle path? A 7-triangle path?
   How many matches would Kiri need to make a 20-triangle path?
3. Let students work out the number of matches needed for the 20th term. Use think, pair, share to allow students to compare their strategies.
4. Kiri noticed that if she rearranged the matches, she could count them quite quickly. The following picture shows how she rearranged them.
   
   How does Kiri’s method work?.
   How would Kiri rearrange a 7-triangle path?
   What expression would she write to show her calculation? (1 + 7 x 2 or 1 + 2 + 2 + 2 + 2 + 2 + 2 + 2)
    
5. Tell the class that Kiri says that using her method, she can see a shortcut way of counting the number of matches needed to make a 10-triangle path. Get them to write down, using pictures to support their explanation, what Kiri’s short cut method might be.
6. Let’s call Kiri’s method, Kiri’s Rule. Ask:
   Using Kiri’s Rule, how many matches will be needed to make a 20-triangle path?
   Reverse the problem by asking: How big a path can Kiri make with 201 matches?
7. Allow students time to develop an answer and compare their strategies.
   • Do students that relied on repeated addition change to multiplicative strategies with increased demand?
   • Are students able to recognise that the term number is required, not the number of matches?
   • Can students ‘undo’ their previous rules to find the term number?
8. Kiri’s friend Jamie arranged his matches differently. His pictures looked like this:
   
   What is Jamie’s Rule?
   What is Jamie’s picture for a 12-triangle path?
   What expression could Jamie write for the 12-triangle path (Term 12)
   How are 3 + 2 + 2 + …+ 2 and 3 + 11 x 2 the same?
9. Jamie says that using his method, he can see another short cut way of counting the number of matches needed to make a 10-triangle path. Get the class to explain, using written and/or verbal language, what Jamie's strategy is. Some students may benefit from, or prefer to use, pictures to support their explanations.
   How many matches will be needed to make a 20-triangle path?
   How big a path can Jamie make with 201 matches?
10. Get the students to explain how Kiri’s Rule is different and the same compared to Jamie’s Rule.
11. Ask the class: How would Kiri and Jamie explain to someone else how they could find the number of matches needed to make a path consisting of any number, say 1000, of triangles?

Extension idea:

Vey-un has another way to work out the number of matches for a 10-triangle pattern. He writes 10 x 3 – 9 and gets the same number of matches as Kiri and Jamie, 21.

Ask students to explain how Vey-un’s strategy works. What do the numbers in his calculation refer to?

[Vey-un imagines ten complete triangles that require 10 x 3 = 30 matches to build. He imagines that the ten triangles join and that creates nine overlaps. He subtracts nine from 30 to allow for the overlapping matches.]

At this stage, it may be appropriate to revisit or introduce the concept of “BEDMAS”. The acronym BEDMAS signifies the order in which operations should be carried out in an equation: brackets, exponents, division and multiplication in the order that they occur, and then addition and subtraction in the order that they occur. Ask your students to solve 10 X 3 – 9 by doing the multiplication first, which is the correct way (i.e. 30 – 9 = 21), and then by doing the subtraction first (i.e. 10 X -6 = -60). If negative numbers are beyond the knowledge of your students at the time of teaching, then you should adjust the numbers in the equations you provide. The key teaching point is that BEDMAS is used to guide us when solving problems with more than one sign. This is important because the order that we carry out number operations can change the outcome of a problem.

Session 2: Square Paths

Here we look at a simple pattern created by putting matches together to form a connected path of squares.

1. Following the same general procedure as above, allow the students to explore ways of counting the number of matches that are needed to make square paths. Present the students with the following picture.
   
2. Have your students construct a 4-square and 5-square path with matches or by drawing. Focus on how many extra matches were added each time. Where are the additional matches located?
3. Ask your students how they could develop a quick and easy way of finding the number of matches needed to make a 20-square path.
   What would Kiri, Jamie and Vey-un do for this square pattern?
4. Let the students work in groups of two or three. Ask the groups to make a picture showing how the 20-square path is made. They can experiment with the provided materials and draw different representations of the pattern. Prompt the students with the following questions: 
   Do you need to draw every square?
   Is there only one possible way to look at the pattern?
   What might some of the other ways look like?
5. Some pictures will be very helpful in counting the number of matches needed to make a 20-square path – some will not. Have the students choose the picture that they think best explains how successive square paths are made up AND gives a quick and easy method for counting the matches needed for a 20-square path. If there is a wide variety of strategies being presented in the group, ask students to share and justify their strategy with a peer who has developed a different strategy. Share the strategies back to the whole class and validate all thinking. Note the cumbersome nature of repeatedly drawing squares and repeatedly adding three matches.
   What is a more efficient way to draw or calculate the total number of matches?
6. Have the students use their ‘best method’ to verify that 61 matches are needed to make a 20-square path.
7. Compare the way the rules might be written:
   Kiri [1 + 20 x 3]                      Jamie [4 + 19 x 3                    Vey-un [20 x 4 – 19]
8. Students can use these methods or their own ways to predict the number of matches needed to make 14-, 36- and 100-square paths.
9. Ask them to write down how they would use their method to count the number of matches needed to make a square path consisting of any number of squares, say 1000 squares. Depending on the comfort of students with their rules you might use algebraic notation to represent the word rules:
   Kiri [1 + 3n]                                  Jamie [4 + 3 (n-1]                   Vey-un [4n – (n-1)]
10. Reverse the problems so students must work out the term number for a given number of matches. 
    How many squares are in a square path with 31, 304 and 457 matches?
    How many matches will be left over if you make the biggest square path that you can with 38, 100 and 1000 matches?
11. Are students able to ‘undo’ their rules to find missing terms?
    Kiri calculates “One plus three times the term number” to find the number of matches.
    If Kiri knows the number of matches, how should she undo her rule to find the term number? [Note that the order of undoing is important, subtract one then divide by three.]

Session 3: House Paths

The ideas learnt in the last two sessions are reinforced here using ‘house paths’.

1. Use the techniques developed in the last two sessions to explore the following problem:
   A new matchstick path is being designed. It is called a house path. The first three terms are shown below. Develop a counting rule, that is, a short-cut way of counting the number of matches needed to make a 1000-house path.
2. Have the students illustrate how they developed their counting rule. They could do this, by using pictures, words or numbers (or some combination of these).
   Do you need to draw every house?
   Do you need to add on 999 times?
   What do you think Kiri, Jamie and Vey-un might do with this pattern?
3. Get the class to discuss the various approaches that were used and methods that were obtained.
4. Allow time for the class to write up its conclusions about the most efficient strategies.
   
5. Latitia has 503 matches. How many houses are in her path if she uses all the matches? Will she have any matches left over?

Session 4: What’s My Path?

Next, the ideas of the first three sessions are extended and reinforced in another context. This time the problem gives a rule and the students find the pattern.

1. Give students the following problem:
   My friend made a picture of a pattern found in the local community that showed how her fifth matchstick path was made. She named it:
   5 lots of 4 and add 2 (this was the counting rule used to make the path)
   She sent it to me via email. However, I was only able to read the name of the path and not see the picture!
   Make some possible pictures that she could have sent.
2. It is worth noting that there are many answers to this. So even if two groups get a different answer, they may still both be correct.
   We have many different pictures that match the word rule. How are they different and how are they the same?
   [The common property is that the pattern starts with two matches and build on using four matches for each additional shape]
3. Examples might include the patterns shown on the rest of PowerPoint One (shown below).
   
   
4. Allow the class time both to report back and discuss their solutions, and to write up what they have discovered.
5. Olika wanted to make a pattern using the n-rule. N means any number you give her, say 1000, 53 or 214. 
   Can you draw a pattern that matches this rule?
   “n minus one then multiplied by five then add six”
   What might the pattern look like?

One possible answer is: 

Session 5: Other Ways of Seeing Things

In this session, the concept of a relation is explored with a more complicated spatial pattern.

1. Show the class the pattern below that is made up of matches. The 1st, 2nd, and 3rd terms of the sequence are shown.
   
2. Challenge the students with this problem:
   Find many different ways to work out the total number of matches in Term 10.
3. Remind students about the ways that Kiri, Jamie and Vey-un represented their patterns, including rules that work for any term.
4. Let students work in pairs or threes. Ensure they record their thinking using diagrams and expressions. Do your students:
   • Look for the growth between terms, i.e. 12 matches.
   • Create tables of values to represent the number of matches for each term
   • Use multiplicative strategies to predict the number of matches for term 10
5. Gather the class to process the ideas. Highlight the efficiency of multiplicative strategies such as 10 x 12 – 8 and 4 + 9 x 12 compared to additive strategies like 4 = 12 + 12 + …
6. Ask students to connect the numbers and operations in their expressions to the figural pattern of matches.
   Why is the number of matches increasing by 12 each term?
   How many groups of 12 matches will be in the 10th term?
   Why does Kiri subtract 4 at the end?
7. How could our rules be used to predict the number of matches needed for Term 23? Term 101? Term n?
8. If Taylor uses 604 matches to build a figure in this pattern, what Term does she make?
9. To assess the ability of students to personally make predictions and create general rules pose this assessment task. 
   Here is a pattern of growing stars made with matches.
   
   How many matches are needed to make Term 15, that has 15 stars?
   Can you write a rule for the number of matches needed to make Term n, any term?
   If you have 244 matches, what is biggest number of stars you can make in this pattern?
10. To further engage students in a real-life context asj them to research repeating patterns from other cultural backgrounds. 

Session 1

In this session students learn to use a cup containing cubes to represent a variable.

1. Put two plastic cups of different colours on a table. Tell the students that you are going to put 12 cubes into the cups. Ask, “How many cubes might go in each cup?”

2. Draw up a table of values to organise the students’ responses. Note that students frequently neglect the options that have zero cubes in a cup. This task is an excellent opportunity to develop the concept of zero as the numbers representing ‘nothing of something.’ 

   Blue	Green
   0	12
   1	11
   2	10
   3	?

3. Tell the students to draw a graph to show the relation between the number of cubes in the blue cup and how many are in the green cup. Ask them to predict what the graph might look like. Students might hand draw the graph or use a spreadsheet like Microsoft Excel or Google Sheets to complete it. If necessary, you could model the construction of a graph, and then have students create their graphs independently or with their peers. This could also be done as a whole-class teacher-modelled activity.
   Ask students to explain why they think the points on the graph lie along a downward sloping straight line. They might notice that the value of the green cup variable goes down by one as the value of the blue cup variable goes up by one.
   

4. Using a range of different coloured cups and different numbers of cubes pose similar problems asking the students to come up with a table of values and a graph to represent the relations. The table below shows four examples of possible problems. The students should model the situation with actual cups and cubes to come with ordered pairs such as (1,3) to represent possible values that the variable may assume. Note that you are dealing with discrete variables (i.e. random variables that can take only distinct values, usually whole numbers). Therefore, the numbers of cubes should be whole numbers. Some students may consider fractions of cubes. Examples of useful relations might be:

   The red cup has two more cubes than the blue cup. This linear relation is effectively r = b + 2	Each blue cup has the same number of cubes. The number of cubes in the yellow cup equals the total number in both blue cups. This linear relation is effectively  y = 2b (b multiplied by 2)
   There are 18 cubes in total. Each yellow cup holds the same number. This linear relation is effectively 18 = r + 2y	The number of cubes in the yellow cup equals the total number of cubes in all the blue cups. This linear relation is effectively y = 3b (b multiplied by 3)

5. Note that in some of these relations, an infinite number of whole number values could be put in the table. For example, in the problem with one yellow cup an three blue cups, the table could read:

   Blue cup	Yellow Cup
   0	0
   1	3
   2	6
   3	9

6. Ask the students to come up with rules that describe the relation. If necessary, model coming up with a rule as a class. You could organise students to work in tuakana-teina relationships, and give students the option to work with the teacher for more direct support. For the relation above this might be, “There are three times as many cubes in the yellow cup as there are in each compared to the blue cup.” Algebraically, this might be recorded as y = 3b, though this is not a learning intention for students at this level. Using algebraic conventions to represent the rule for a pattern could be offered as an extension task. Choose a couple of relations for students to graph. Look at the pattern formed by points on the graph and ask students to explain why the graph is linear (it points in a straight line).
7. Pose real life scenarios for students to support them to understand the significance of relationships with variables. Model each scenario with cups and cubes, with a particular coloured cup representing the number of items possessed by each person.
   • Tammy is four years older than Hosepha. How old might both people be?
   • Anshul has three times as many toy cars as Kahu. How many toy cars might each boy have?
   • Altogether Liam and Moana have 24 video games. Moana has twice as many video games as Liam. How many games might each person have? (Note that zero values are not possible in this problem. Why?)

Session 2

In this session students explore the effect of operations on variables. Inverse operations are presented as “doing and undoing” processes.

1. Pose “think of a number” problems for students that result in some unexpected answers at the end. Encourage the students to reason why that occurs and discuss with a partner. The processes involved can be modelled using cups and cubes. Begin with a problem where the use of inverse operations is obvious. Note that the algebraic representation is not expected though you might use an empty box as n for a more accessible representation.

   Instructions	Cups and cubes model	Algebraically
   Think of a number		n
   Add five		n + 5
   Take away your starting number		5

   Ask: Why does everyone get an answer of five, no matter what starting number they thought of?
   Do your students realise that subtracting n undoes the adding of n in the first place?
    

2. Develop more complex examples. Encourage the students to model the steps with cups and cubes to explain the effect of the operations.
   For example:

   Instructions	Cups and cubes model	Algebraically
   Think of a number greater than 5		n
   Take away four		n – 4
   Double the answer		2 (n- 4) = 2n – 8
   Add ten		2n + 2
   Halve the answer		n + 1
   Take away your starting number		1
   Your answer is one!

   Instructions	Cups and cubes model	Algebraically
   Think of a number		n
   Add three to the number		n + 3
   Double the answer		2(n + 3) = 2n + 6
   Take away four		2n + 2
   Halve the answer		n + 1
   What number did you start with? Your final answer was one more than your starting number.

3. Discuss how each activity works. Look for students to explain that some operations undo others. In particular, subtraction undoes addition (and vice versa) and division undoes multiplication (and vice versa). 
   Tell your students that addition and subtraction, and multiplication and division are inverse operations. With the class, come up with a list of metaphors that describe inverse relationships (e.g. turning a light switch on and off).
   Students also need to recognise when an operation is only partly undone. For example, with 3n + 6 dividing by three will undo multiplying n by three, but the addition of six is not completely undone. Demonstrate this for students.
4. As a class, come up with a new (or several) “think of a number” problem(s) and represent the values in a table and graph. Highlight that the relationship on the graph is linear (i.e. is represented by a straight line). Emphasise the use of inverse operations, and draw on students’ experiences of working with cups and cubes. Keep the equations simple by using only two different operations, and numbers below 10 (e.g. 4n + 7). The letter ‘n’ can be used to keep the equation(s) consistent with what has previously been covered in the lesson.
5. Invite the students to develop their own “think of a number” problems. This could be done in pairs, small groups, or independently. Emphasise the use of inverse operations. At this stage, students are not expected to find the resulting answer of linear equations, rather they are expected to demonstrate their understanding of the effects of operations. Their attempts can be set as examples for other students to explain. Look for the following:
   • How complex are students’ attempts at inverse operations? In the early stages you will find that students tend to immediately undo a previous operation.
   • How comfortable are your students with variables being unknown?
   • Are they able to recognise the parts of an expression that are variable (the cups) and that are fixed (the cubes)?
   • Can they control variables and numbers under the operations? Division is particularly challenging. For example, 3n + 6 divided by three requires each part, 3 cups and 6 cubes, to be divided separately then recombined.

Session 3

In this session students model equality with cups and cubes models. They investigate operations that can be performed on both sides of the equation, that simplify the relationship while maintaining equality.

1. Begin with simple equalities such as:

   Each red cup has the same number of cubes and each blue cup has the same number of cubes. Which collection, left or right,  has the most cubes?
   Look for students to realise that structurally the collections are the same (Two blue cups and three red cups on each side). This can be provoked by putting different numbers of cubes into the cups, e.g. 3 cubes in each red cup, 8 cubes in each blue cup. The equality of the collections is preserved no matter what numbers are used.

2. Ask: Could I remove cups from both collections and the total number of cubes would remain equal? What could I do?
   Look for students to realise that taking away the same cups from each side leaves the equality maintained. Algebraically that is alike 3r + 2b = 2b + 3r so 2r + 2b = 2b + 2r (subtracting one red cup from each side)
   Also consider what cannot be done. For example, removing a red cup from the left collection and a blue cup from the right collection does not maintain the equality. 

3. Provide other examples where applying the same operation to both sides makes finding possible values for the variables much easier.

   Each yellow cup holds the same number of cubes as every other yellow cup.
   Each blue cup holds the same number of cubes as every other blue cup.
   The left collection of cubes equals the right collection of cubes.
   What numbers of cubes could be in the yellow and blue cups?
   
   
   Simplifying both sides by removing the same cups makes the problem much easier.
   
   In this case students are left with the equality that one blue cup equals two yellow cups (b = 2y). An infinite set of solutions like (0, 0), (2, 1), (4, 2),… is possible.
    

4. Get students to connect the concepts of variable and equality using group worthy problems like:

   
   Each cup of a given colour, in both collections, must contain the same number of cubes, e.g. all reds hold 4 cubes, all yellows hold 3 cubes.
   What numbers of cubes could be put in each cup so that the two collections contain the same total number of cubes?
   Students might realise that the number of cubes placed in the red cups is irrelevant to the problem since it is the equivalence of two yellow cups to one blue cup that determines whether or not the collections are equal. They are likely to arrive at this conclusion by experimenting and looking for commonality among the solutions.

5. Recording their solutions systematically will help:
   Solutions for r = 1                              Solutions for r = 2                 Solutions for r = 3
   y = 0 so b = 0                                      y = 0 so b = 0                         y = 0 so b = 0
   y = 1 so b = 2                                      y = 1 so b = 2                          y = 1 so b = 2
   y = 2 so b = 4                                      y = 2 so b = 4                          y = 2 so b = 4
   y = 3 so b = 6                                      ....                                          ....
    
6. Explore other group-worthy equivalence problems such as:
   •                              
     What numbers of cubes for each colour of cup will make each collection equal?
     (Two reds must equal one blue plus six)
     What is in common with these solutions? 
      
   •                                
     What numbers of cubes for each colour of cup make each collection equal? (One green plus one blue must equal one yellow plus three)

Session Four

In this session cups and cubes models are created to solve problems more traditionally associated with algebra. Students attempt to find specific unknowns from the information they are given.

1. Start with this problem:
   Manaia began the weekend with some dollars in his money jar.
   He worked all day on Saturday weeding Mr Barkley’s gardens.
   After he was paid Manaia saw he had five times as much money as he had to start with.
   On Sunday, he delivered advertising, and made an extra $12.
   By the end of the weekend he had a total of $72.
   How much money did he have at the start of the weekend?
2. Ask students: How could we use cups and cubes to help us solve the problem?
3. Students might suggest using a cup to represent the amount of money Manaia had at the start. They might then track what happens to the model as Manaia earns money.
   
   Starts with some dollars…      Then has five times as much…Then adds $12 to that amount
    
4. Set up an equality like this (Equivalent to 5m + 12 = 72):
   
    
5. Ask: What can we do to make this equation simpler?
   Students should suggest some undoing, using inverse operations. The order is important. The undoing needs to occur in the reverse order to the first operations.
   Take $12 off each side:
   
   Divide both sides by five:
   
    
6. Manaia had $12 at the start of the weekend. Check the answer by acting out the original problem. Put 12 cubes in each cup then work through five times as much then adding $12.
   Has Manaia got $72 or are we incorrect?
   You might use a calculator to check (5 x 12 + 12 = 72)
7. Pose this problem for the students to solve in pairs. The numbers are smaller, but the operations are more complex. This problem could be adapted to better reflect your classroom context.
   Jodie collected lemons to squeeze juice. She started with a few lemons.
   After she visited her Nana’s tree, Jodie had six times as many lemons as she had to start.
   She got another 15 lemons from her neighbour.
   Jodie’s Mum was a bit worried about her lemon collecting habit. She told Jodie to share her lemons equally with her two sisters.
   “That’s fair,” said Jodie, “I still have 13 lemons to make juice.”
   How many lemons did Jodie have at the start?
8. Watch as your students try to model the problem.
   • Do they set up a cups and cubes model or find another strategy, e.g. trial and improvement?
   • Do they control the order of the inverse operations?
   • Do they check to see that their solution meets the conditions of the problem?
9. Gather the class to discuss strategies, and check the solution of four for the starting number of lemons.
10. Give your students Copymaster 1 to work through.  They can use cups and cubes if they want to model the problem though drawing diagrams is a useful alternative.
11. Students share their strategies with the class and justify their thinking.

Session 5

In this session students use the cups and cubes model to solve problems from growth patterns. Matchsticks are used to create the figurative patterns.

1. Connect the students’ understanding of equivalent structures with rules to describe relations. Pose problems like:
   Petra and Clive are looking at this matchstick pattern:
   
   They have worked out that it takes 25 matches to make 12 triangles in this way. Their teacher has challenged them to work out how many matches 100 triangles might take to make.
   What rules can you find to help Petra and Clive so they do not have to build 100 triangles?
   Students are likely to come up with different direct rules that describe the relation between the number of triangles and the number of matches. For example:
   • The first triangle took three matches. Each triangle after that took two matches. So to make 100 triangles takes 99 x 2 + 3 matches.
   • There was one match to start with and each triangle took two more matches. So 100 triangles takes 100 x 2 + 1 matches to make.
   • Each triangle takes three matches to make but when two triangles are joined there is one extra match. So to make 100 triangles takes 100 x 3 - 99 matches.
2. Ask the students to explain where the numbers come from in each person’s rule. Check to see that all three rules give the same answer to the number of matches. Use the explanations to model the structure of each rule using a cup to represent the chosen number of triangles.
   • Take one off the number of triangles (99), double it, and then add three. 
                            
      
   • Take the number of triangles (100), double it, and then add one.
     
      
   • Take the number of triangles (100), multiply by three, then take away one less than the number of triangles (99). Note 99 is the number of joins of two triangles and taking away one less than n is like taking n away but leaving one behind.
     
     With the cups and cubes model it is easier for students to appreciate the structural similarity of the rules in that one model can be converted to the others. For example, in the first rule if two of the three cubes are used to replace the two cubes taken out then the model becomes the second model. This is equivalent to proving physically that 2(n-1) + 3 = 2n + 1
3. Provide the students with a related stick problem and ask them to find as many rules as they can. Tell them to then explain the equivalence of the rules using cups and cubes models. For example:
   
   How many matches would it take to make 20 houses in this pattern?
   Rules might include:
   • 19 x 5 + 7 (seven for the first house, five for each house after that)
   • 20 x 5 + 2 (five for each house plus two matches to start)
   • 20 x 7 – 19 x 2  (seven for each house less two matches for each join)

Session 6 (extension session)

In this session students learn how cups and cubes models can represent why number relationships work.

1. Get the students to apply the structural strategies they have to problems that involve proof. Begin with simple properties of consecutive numbers.
   Take any three consecutive numbers, e.g. 3, 4, 5.
   If you add the numbers (3 + 4 + 5 = 12), this equals three times the middle number (3 x 4 = 12).
   Does this work for any set of three consecutive whole numbers? Why?
2. Invite students to explain why the rule holds for any set of consecutive whole numbers, and to model their explanation with the cups and cubes model.  Let n be the first number:
   
   Students may recognise that both collections total three lots of the first number plus three. Algebraically this could be written as, n + (n + 1) + (n + 2) = 3n + 3 = 3 (n + 1)
3. Pose another problem involving consecutive numbers and ask the students to explain why the property holds irrespective of which four numbers are chosen.
   Choose any four consecutive odd numbers, e.g. 3 + 5 + 7 + 9.
   Add the two outside numbers, e.g. 3 + 9 = 12.
   Add the two inside numbers, e.g. 5 + 7 = 12.
   Are the sums always equal no matter what consecutive odd numbers you choose? Why?
   Would this work for consecutive even numbers? Why?
    

4. Pose other more complex problems that can be modelled with cups and cubes.
   For example: 
   Choose any two single digit numbers, e.g. 3 and 8 (modelled by two different cups).
   Use the digits to make two different two-digit numbers,
   e.g. 38 and 83, 38 = 10 x 3 + 8, 83 = 10 x 8 + 3

   Add the two sums, e.g. 38 + 83 = 121
   Divide the answer by 11, e.g. 121 ÷ 11 = 11
   The result is always the sum of the two digits, e.g. 3 = 8 = 11.
   Does this always happen? Why?

   Hint: If b is the first digit and r is the second digit, then a model of 10b + r looks like this. 
   What will the model of 10r + b look like?

   
   Why will the sum of 10b + r and 10r + b equal 11 x (b + r)?