Session One

Begin each session in this unit with an addition/subtraction grid. This session gives you details about how to introduce the activity. Grids for the other sessions are provided in PowerPoint 1. Try to limit this activity and discussion of how students found the answers to no more than ten minutes.

1. Show Slide One of PowerPoint 1.
   
   Discuss how to complete the grid. The answers to the additions go in the body of the table. For example, 7 + 6 = 13 so 13 can be placed in the second cell in the third row.
   Some of the addends (numbers to add) are missing.
   How will you workout what numbers they are?
   Students might recognise that 2 goes in the bottom of the left-hand column because 7 + 2 = 9. Students check with a buddy that they both understand how to complete the grid. 
2. Let students complete the grid. Some students enjoy the challenge of improving on their time from day to day, but others may not. Students can record their time each day if that motivates them.
   Use the animation of Slide One (mouse clicks) to show the answers and how those answers can be determined from the information that is given.
3. The key idea in this lesson is to solve addition and subtraction problems using place value. Make sure that you have physical materials that represent the place value structure of whole numbers, such as Place Value Blocks, beaNZ in canisters, iceblock sticks in bundles, or Place Value People.  Money is not a proportional representation, and one cent coins are no longer used. Use problem stories other than those involving money, if possible. A suitable problem could be:
   
   On her birthday all Aniwa wanted was her favourite seafood. She received 56 pipis in the morning and 37 kuku (mussels) in the afternoon. Because of the numbers she suspected that someone snuck a few for themselves before giving them to her. However, she was happy because she still had plenty to share with her whānau and friends. How many shellfish did she receive?
   
   Represent each calculation using both the physical materials and empty number lines. For example, 56 + 37 = 93 can be represented as:
              
   56 equals 5 tens, and 6 ones                     Adding 30 gives 86, 8 tens, and 6 ones
             
   Adding 7 gives 8 tens, and 13 ones           10 ones make 1 ten so the answer equals 93
   

Another problem could be:

Korimako was organising his first local kapa haka festival. He was amazed at the number of groups that entered. There were 57 senior groups and 45 junior groups.  How many groups registered altogether?

Session Two

1. Use Slide Two of PowerPoint 1 to give students an addition grid to solve. The animation provides the logical sequence to find the addends and sums (Use mouse clicks).
2. The key idea in this session is using tidy numbers with compensation to solve addition and subtraction problems. Consider using proportional place value materials rather than money, and changing the contexts of the problems to be encouraging and relevant to your students.
3. Pay particular attention to the inverse compensation needed for subtraction.
   For example, consider 72 – 38 = □  (in an appropriate story context). An example could be: John had 72 marbles but over two weeks he lost 38 marbles to his friends. How many does he have now?
   With place value blocks the problem might be represented as:
            
   72 equals 7 tens, and 2 ones                    Subtract 40 (4 tens) leaves 3 tens, and 2 ones (32)
   
   Compensating for removing 40 instead of 38 gives 3 tens and 4 ones (34)
   The same operation on an empty number line looks like this:
   
4. Pose problems with three-digit whole numbers as well, such as:
   There are 725 trout in Lake Kahurangi at the start of the fishing season.
   297 of the trout are caught.
   How many trout are left?
5. Let students practise from Copymaster 1. Ask students to share their strategy with a partner.

Session Three

1. Use Slide Three of PowerPoint 1 to give students an addition grid to solve. The animation provides the logical sequence to find the addends and sums (Use mouse clicks).
2. The key idea in this session is about using the inverse relationship between addition and subtraction, particularly solving subtraction problems by adding on. Use proportional place value materials rather than money. Use problems with contexts that are of interest to your students.
3. It is important that students understand why it is possible to solve a problem like 95 – 68 = □ by solving 68 + □ = 95, as well as developing the procedural fluency in doing so.
                 
   95 equals 9 tens and 5 ones                        If 68 was subtracted there would be ? left
   
   That means 68 + ? = 95
   In empty number line form the problem is represented like this:
   
   
4. Let students practise from Copymaster 2 and share their thinking with a partner.

Session Four

1. Use Slide Four of PowerPoint 1 to give students an addition grid to solve. The animation provides the logical sequence to find the addends and sums (Use mouse clicks).
2. The key idea for session 4 is about students making sensible strategic choices about how to solve addition and subtraction problems. Encourage students to use mental and written methods. Only use proportional place value materials when students need additional support. Change the contexts of the problems to be about items that are of interest to your students. Ask the students to provide contexts also. 
3. Discuss the criteria for deciding which method/s are the best for certain calculations. Encourage students to make up problems that each strategy (place value, tidy numbers, inverse thinking) would be useful for.They might conclude:
   • Place value works on any numbers but is more difficult where renaming is required.
   • Tidy number strategies work best when the one or both numbers are close to a tidy number (usually a decade or century).
   • Inverse thinking strategies work on any numbers but are especially useful if renaming is needed for subtraction.
4. Equal adjustment is another strategy where the addition form of equal adjustment is conceptually easy, but the subtraction is not. Choose whether, or not, to offer those strategies to your students but do not invest too much time in doing so. Here are examples:
   • Addition 48 + 34 = □ 
                                 
     48 add 34                                     has the same sum as 40 + 32 = 72
     
     
   • Subtraction 81 -58 = □
              
     The difference between 81 and 58 is the same as the difference between 83 and 60. 
     83-60 = 23.
     
     
5. To practise applying addition and subtraction strategies ask students to work on these Figure It Out activities:
   • Tidying Up, from Number Sense and Algebraic Thinking, Level 3, Pages 2-4,
   • The Strategy Strut, from Number, Level 3, Book 3, Pages 6-7,
6. Another useful strategy is to split the smaller number into tens and ones. For example 81 - 58 becomes 81 - 50 - 8.  81 - 50 is 31 and 31 - 8 is 23 so 81 - 58 = 23

Session Five

1. Use Slide Five of PowerPoint 1 to give students an addition grid to solve. The animation provides the logical sequence to find the addends and sums (Use mouse clicks).
2. In this session, the key idea involves use of standard written forms for addition and subtraction. Students should also use calculators as another way to find answers to addition and subtraction problems. When solving problems use the simplest written form for addition rather than the expanded form.
3. Use proportional place value materials when developing the written forms so students understand what is occurring with the quantities. Alongside learning for understanding give students sufficient practice to develop fluency. Here are examples:
   • Addition
     
   • Subtraction (using decomposition)
     
4. Let students practise from Copymaster 3.

Getting Started

The purpose of this session is to explore the range of strategies already used by students to solve addition and subtraction problems. This lesson will enable you to evaluate which strategies need to be focused on in greater depth. In turn, you will identify students in your group as "expert" in particular strategies. There are two problems given as examples for exploration. You may want to use further examples of your own. Consider adapting the contexts used in these problems to further engage your students.

1. Problem 1: Sarah has $288 in the bank. She then deposits her pay for $127 from her part time job at a cafe. How much does she have now?
   Ask the students to work out the answer in their heads or by recording in some way. Give the students plenty of thinking and recording time. Ask the students to share their solutions and how they solved the problem with a peer. The following are possible responses:
   
   Place value (mentally, possibly with the support of equations on an empty number line):
   288 + 127 is just like 288 + 100 +20 +7. So that’s 388… 408… 415.
   
   Tidy numbers (mentally, possibly with the support of equations on an empty number line):
   If I tidy 288 to 300 it would be easier. To do that I need to add 12 to 288, which means I have to take 12 off the 127. So that’s 300 plus 115. 
   
   Algorithm (usually written):
   Students may visualise or record a written algorithm like this:
   
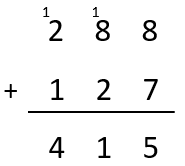
   Understanding is revealed by the language used to describe the strategy, such as, “8 plus 7 equals 15. I wrote 5 in the ones place and carried the extra ten into the tens place because 15 is made up of 5 and 10 and I can only record one digit in the ones place.”
   
   As different strategies arise ask the students to explain why they chose to solve the problem in that way. Accept all the correct strategies that are elicited, recording the strategies to reflect upon later in the unit on the class T chart (under the addition heading). You might also ask students to model how their strategies work with place value materials. Note that folding back to justify a strategy is often more difficult than performing the strategy.
    
2. Problem 2 Sarah has $466 in her bank account and spends $178 on a concert ticket. How much money does she have left in her bank account?
   Ask students to solve the problem mentally, giving them plenty of thinking and recording time. Then ask students to share their solutions and how they solved the problem with a peer. Possible responses are:
   
   Reversibility (adding on to find the difference with recording to ease memory load):
   $466 - $178 is the same as saying how much do you need to add to $178 to get $466. $178 plus $22 makes $200, plus $200 more makes $400 plus $66 makes $466. If you add up $22 plus $200 plus $66 you get $288.
   
   
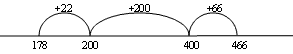
   Subtracting a tidy number then compensating 
   $466 - $200 = $266. I took off $200 instead of $178 so I need to ‘pay back’ $22. $266 + $22 = $288.
   
   Equal additions:
   You round the $178 to $200 by adding $22. $466 - $200 is $266. Then you put on $22 to keep the difference the same, so it’s $288.
   
   Algorithm (usually written):
   Students may visualise or record a written algorithm like this:
   
   
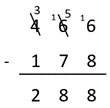
   Understanding is revealed by the language used to describe the strategy, such as, “6 minus 8 doesn’t work (ignoring integers) so I changed one ten from the tens column into ones to make 16. I wrote 16 in the ones place and took one ten off in the tens place…”
   
   As different strategies arise, ask the students to explain why they chose to solve the problem in that way. Accept all the correct strategies that are elicited, and justified, recording the strategies to reflect upon later in the unit (under the ‘subtraction’ heading on the class T chart). You might also ask students to model how their strategies work with place value materials. Note that folding back to justify a strategy is often more difficult than performing the strategy.
   
   Subtraction strategies tend to be more difficult to control than addition strategies, given comparable numbers. Look out for students compensating the wrong way (taking more off) in the tidy number strategy and making errors when using the algorithm.
   
   Use your observations to plan for your subsequent teaching from the exploring section outlined below.

Exploring

Over the next two to three days, explore different strategies for addition and subtraction of whole numbers. Give the strategies a name so students can tell others which strategy they are preferencing for a given problem. Highlight when certain strategies are most efficient, for example, In the problem 357 + 189 tidy numbers would be a useful strategy because 189 is close to 200.

Follow a similar lesson structure each day to the introductory session, with students sharing their solutions to the initial questions and discussing why these questions lend themselves to the strategy being explicitly taught. Conclude each session by asking students to make statements about when the strategy would be most useful and why the certain problem is appropriate, e.g., tidy numbers when one number is close to 100 or 1000, standard place value (hundreds, tens, and ones) when no renaming is needed and reversibility when neither of the other two numbers are easy for subtraction. It is important to record examples of strategies as they will be used for reflection at the end of the unit. Some strategies may require more teaching time, greater use of materials, and more scaffolded and individualised teaching. Ensure that students who demonstrate proficiency with the strategies early on in each session have adequate opportunities for practice, extension, and supporting their peers (if appropriate).

The questions provided are intended as examples for the promotion of the identified strategies. If the students are not secure with a strategy you may need to make up some of your own questions to address student needs. Consider adapting the contexts reflected in these problems to further engage your students.

Tidy numbers then compensating

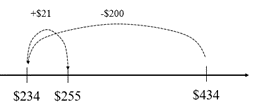
1. Room 9 are selling muesli bars at lunchtime to raise money for their camp. They had 434 at the beginning of lunchtime and sold 179, how many did they have left to sell?
   The tidy numbers strategy involves rounding a number in a question to make the question easier to solve. In the above question, 179 can be rounded to either 180 (by adding 1), or 200 (by adding 21). If 200 is subtracted (434 – 200 = 234) then the result is 21 less than the answer. 234 + 21 = 255. An empty number line shows this strategy clearly:
   
   For addition questions, one addend can be tidied by taking from the other addend. Alternatively, both addends might be tidied, and compensation used to adjust for the tidying.
2. The following questions can be used to elicit discussion about the strategy.
   • What tidy number could you use that is close to one of the numbers in the problem?
   • What do you need to do to the other number if you tidy up this number? Why?
   • Why is this strategy useful for this problem?
   • What knowledge helps you to solve a problem like this?
3. If the students do not understand the tidy numbers concept, use place value equipment (place value blocks, place value people, beaNZ) and/or an empty number line to model the problems physically. Students should be encouraged to record equations and number lines to track their thinking and reduce load on working memory.
4. Use the following questions for further practice if required:
   • Ariana has scored 739 runs for her cricket club this season. Last season she scored 294, how many did she score in total in the last two seasons?
     Shifting six between the addends gives 739 + 294 = 733 + 300 = 1033.
   • Nigel sold his guitar for $587 and his amp for $395. How much money did he make from both sales?
     Rounding 587 to 600 and 395 to 400, then compensating gives 587 + 395 = 600 + 400 – 13 – 5 = $982.
   • Farmer Samsoni has 1623 sheep, and he sells 898 sheep at the local sale. How many sheep does he have left?
     Rounding 898 to 900 gives 1623 – 898 = 1623 – 900 + 2 = 725
   • Other examples might be:
     568 + 392
     661 - 393
     1287 + 589
     1432 - 596
5. Note that the problems posed here are using a tidying up strategy rather than tidying down i.e. 103 down to 100 as in these situations place value tends to be a more useful strategy.

Place Value (written algorithm)

1. For the community hangi, 356 potatoes are peeled and there are 233 left to be peeled. How many potatoes will there be altogether?
   The place value strategy involves adding the ones, tens, hundreds, and so on. In the above problem:
   300 + 200 is added
   Then 50 + 30
   And finally 6 + 3
   As an algorithm the calculation is represented as:
   
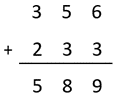
2. The following questions can be used to elicit discussion about the strategy:
   • How can you use your knowledge of place value to solve this problem?
   • Why is this strategy useful for this problem?
3. If the students do not understand the strategy, use place value equipment to show the problems physically. Students will find it useful to record and keep track of their thinking .
4. Use the following questions for further practice if required:
   • Zac has $498 available on his eftpos card and spends $243 on a new BMX bike, how much money does he have left?
   • Other problems might be:
     3221 + 348
     4886 - 1654
     613 + 372
     784 – 473

Reversibility (adding one rather than subtracting to find the difference)

1. Faloa is helping his Mum build a path. There were 438 bricks in the pile and they used 169 of them yesterday. How many bricks have they got left to lay today?
   The reversibility strategy involves turning a subtraction problem into an addition one so the problem above becomes:
   169 + ? = 438
   Using tidy numbers to solve the problem makes calculation easier:
    
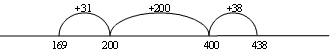
   Or
   
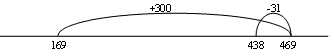
2. The following questions can be used to elicit discussion about the strategy:
   • How could we think of this as an addition equation?
   • What do you need to add to make it easier to solve?
   • How can you keep track of how much you have added altogether?
   • Why is this strategy useful for this problem?
   • What knowledge helps you to solve a problem like this?
3. If the students do not understand the concept, use a number line to show the problems graphically. Students will find it useful to record and keep track of their thinking using a number line.
4. Use the following questions for further practice if required:
   • At the mail sorting office there were 547 letters to be sorted, 268 of these were distributed to private boxes, how many were left to be delivered?
   • The school library has a total collection of 1034 books and 459 are issued at the moment, how many are on the shelves?
   • Other problems might be:
     628 - 342
     537 - 261
     742 - 353
     1521 - 754
     1762 - 968
     1656 - 867

Reflecting

As a conclusion to the week’s work, give the students the following five problems to solve. Pose the problems in contexts that are relevant and engaging for your students. Ask students to discuss, with a peer or in small groups, which strategy they think will be most useful for each problem and justify their view. For some problems many strategies may be equally efficient. After students have solved the problems, engage in discussion about the effectiveness of their selected strategies.

Some students may have a favourite strategy that they use, sometimes to the exclusion of all others. The best approach is to pose problems where the preferred strategy may not be the most efficient. For example, 289 + 748 is most suited to using tidy numbers and compensation.

Problems for discussion
1318 - 747
763 - 194
433 + 452
1993 + 639
4729 - 1318

You might also like to also try some problems with more than two numbers in them, such as:
721 – 373 - 89
663 - 61 - 88
63 + 422 + 49
42 + 781 + 121
84 + 343 - 89

1. Discuss the different strategies explored during the week and ask students to explain in their own words what types of problem each strategy would be useful for solving, and what types of problem each strategy would not be useful for solving. Ask the students to draw a strategy ‘from a hat’ and write questions specific to that strategy for a partner.
2. Conclude the unit by showing the students the questions asked in the initial session again. Discuss whether they would solve the problems in a different way now, and how their thinking has evolved. With a partner, students could create a short presentation demonstrating how they would solve one addition and one subtraction problem, naming the strategies used, and justifying the use of their chosen strategies.

This activity uses interesting real-life large numbers to provide a context for making and solving addition and subtraction problems.
Have the students estimate before calculating.
Questions 1 and 2 may be good challenges as mental calculation for some students. Discuss the “in the head” strategies that some students may have used. Some students may add the thousands first. This is acceptable, for example, “In the thousands, there are three lots of 8 and another 3, that’s 27 thousands. In the hundreds, there is a 6, a 7, and an 8, that’s 21 hundreds. We now have 29 thousand, 1 hundred. Seventeen tens makes another 170. Now we have 29 270. Twenty-one in the ones place will make a total of 29 291 metres.”
You may wish to generate more calculations with additional questions, for example, “What is the difference in height between Mount Everest and Mount Cook?” “Approximately how many times longer than the Clutha is the Nile?”
This activity is a good model to help students generate their own interesting geographical questions.
Use online or book sources, such as atlases or encyclopaedias that feature large numbers.

Answers to Activity

1. 29 291 m
2. 17 573 km
3. These answers are based on measuring from the centre of each circle marking a port (to the nearest centimetre).
a. 1 225 km
b. Approximately 5 250 km

The toroa theme uses an interesting local context to apply addition and subtraction. This sort of context enables the students to understand the problem before deciding on a way to solve it.
The empty (or open) number line offers a diagrammatic way for students to devise and explain a strategy for solving the problems. This visual model also encourages the students to come up with the advanced additive stage strategies described in the Number Framework.
An empty number line marks the steps in thinking used by the students. Unlike the traditional number line, it is not intended to be a calculating tool that uses equal divisions.
Discuss the tidy number strategy that is used in the number line example of Tahi’s flight distance for days 5 and 6. Make sure that the students notice the directional change in the arrows: the 299 is rounded up to 300 and added to 329, and then the arrow is reversed to subtract 1 to adjust the tidy number.
There are other possible number lines apart from those shown in the Answers that can be used to solve each question. The students’ lines should match the thinking strategies they have used and result in the correct answer. Have some students share their ways of thinking.
The key to question 2 is the strategy the students choose to find the birds that fit the conditions. The easiest way, as given in the hint, would be to find 2 numbers in the ones place for each bird on Òriwa’s distance table that add up to the number required in that place and then test to see if the choice is correct. Some students may look at the hundreds place for 2 numbers that add up to either the same or 1 less than the required number, then check to confirm their choice.
Have the students discuss some of the strategies they used to confirm the exact answer.
The best strategy for question 3 is for the students to start from 1 762 kilometres. Students who add the first 5 days again will arrive at the correct answer, but they won’t have used the information in the question to best advantage.
In question 4, the students cannot presume that the question applies to the first 4 days, so they need to find out which 4 days add up to 1 429 kilometres. When they have done this, they may choose to add up the distances for the first 3 of those 4 days. This is fine, but the question is designed to encourage subtraction (1 429 – the fourth day = total of the first 3 of those days).
Ask the students to find a way that makes use of all the information in the question. Discuss the strategies used and encourage the students to use empty number lines as part of their explanation.
Encourage the students to make up their own problems using the toroa context. They should be able to work out their own problem so that they can then explain it to others. Encouraging them to think about and explain the problems they make up will ensure that they do not choose numbers that are ridiculous.

Answers to Activity

1. Answers and possible number lines are:

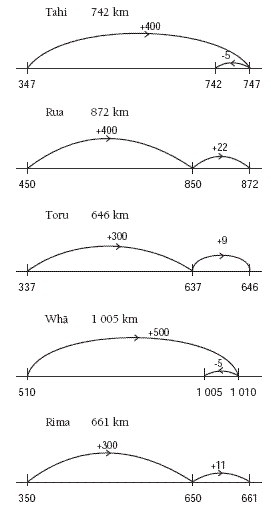
2. a. Rua. (Days 5 and 6)
b. Toru. (Days 9 and 10)
c. Whā. (Days 1–4)
3. 2 412 km. A possible number line is:

4. 1 047 km. (Days 3, 4, and 5)