The numbers get larger
In this unit students, are encouraged to extend their use of part/whole methods from working with small numbers to working with multi-digit numbers. This work follows naturally from the Smart Doubling and Make a Ten units.
- Use part/whole strategies to solve multi-digit addition and subtraction problems.
- Use the most efficient mental strategy for a given problem.
To extend their use of part/whole methods from working with small numbers to working with multi-digit numbers, students need to understand a range of simpler part/whole strategies. These strategies are described in the units Smart Doubling and Make a Ten, and include:
- Working out 38 + 39 by removing 1 from the 38 to leave 37, adding this 1 to the 39 to make 40, then adding 37 and 40 to give 77.
- Working out 38 + 39 by 30 + 30 = 60, 8 + 9 = 17, 60 + 17 = 77.
- Working out 38 + 39 by 40 plus 40 = 80 and then removing 2 (to get to 38). Removing a further 1 (to get to 39). So 80 - 2 - 1 = 87 gives the answer.
- Working out 8 + 5 by removing 2 from the 5 to leave 3, adding this 2 to the 8 to make 10, then adding the 3 to the 10 to give 13.
- Working out 38 + 8 by removing 2 from the 8 to leave 6, adding the 2 to the 38 to give 40, then adding 6 to the 40 to give 46.
The learning opportunities in this unit can be differentiated by providing or removing support to students and varying the task requirements. Ways to support students include:
- using other materials (e.g. hundreds boards, Slavonic abacus, blank tens frames, counters) to show demonstrate strategies and support students' thinking. Some students might be encouraged to move to imaging and mental operations, whilst others might feel the need to fold back to activities
- varying the complexity of the numbers used in each activity
- providing time for students to make up new problems to be solved by their peers
- constructing a shared chart of strategies as they are arise in each session (e.g. a mind map, poster, slide deck etc.). This can be added to throughout the week and used as a tool for supporting students' thinking
- providing opportunities for individual, grouped, and paired work
- strategically organising students into pairs and small groups in order to encourage peer learning, scaffolding, and extension
- working alongside individual students (or groups of students) who require further support with specific areas of knowledge or activities.
The context for this unit can be adapted to increase the relevance of this learning to your students' lived experiences, interests, cultural backgrounds, and learning from other curriculum areas.
Te reo Māori kupu such as tāpiri (add), tango (subtract), and tatau (count) could be introduced in this unit and used throughout other mathematical learning.
You could also encourage students, who speak a language other than English at home, to share the words related to addition and subtraction from their home language.
Getting Started
To start with, students solve addition and subtraction problems involving one single-digit number and one multi-digit number. Once they can confidently solve these, progress to problems that involve two multi-digit numbers.
- Pose the problem:
Minnie has $8 and her grandmother gives her $19 for her birthday. How much money does Minnie have now? - Model the problem on pre-printed tens frames, and have students do the same.
- Encourage students to identify dots that could be moved to make the problem quicker or easier (more efficient) to solve. Note that because pre-printed tens frames are used the dots don’t actually move. For example:
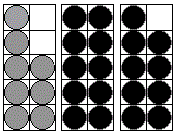 Mentally becomes
Mentally becomes 
- Repeat with similar problems, sharing the Make to Ten strategies used. Record the strategies on your class chart.
Exploring
Over the next 3-4 days pose addition and subtraction problems for the students to work on, individually, in pairs or in a small teaching group. Encourage the progression from using pre-printed tens frames to imagining the tens frames and then to completing the problem mentally.
- Pose the problem:
Malcolm has $27 and he spends $9 on lunch. How much does he have left? Begin modelling this on tens frames, explaining what you are doing, and have students model this, with a partner, using pre-printed tens frames. - Share solutions. Students are likely to imagine the 7 is removed leaving 20, then 2 is removed from one of the tens to leave 18. Other methods are possible.

Pose the following problems for the students to work on. Give the students pre-printed tens frames to help in their solutions, and encourage them to now work independently.
28 + 7, 33 - 6, 24 - 5, 38 - 6, 24 + 9, 33 + 5, 40 - 6
- Have students share their answers with a partner, before going through each problem as a class.
- Pose the following problems. For these problems encourage the students to imagine the tens frames and work independently:
38 + 6, 23 – 8, 44 – 5, 39 – 9, 9 + 34, 3 + 45, 30 – 9
- When the students are able to solve problems involving a single and double-digit numbers extend the problems to involve two 2-digits numbers. Have pre-printed tens frames available. You might have some students working on these 2-digit problems (they could even make up their own) whilst working with other students on more 1-digit problems.
- Pose the problem:
Kiri has 37 Jaffas and 26 wine gums. How many lollies does Kiri have altogether?
 | .gif) |
- Discuss the students’ ideas for solving the problem.
- One strategy involves putting the tens together to get 50 sweets and then combining the 7 + 6 to get 13. The 13 is then added to the 50 to get 63.
- Alternatively they may combine the tens to give 50, then put the 9 with the 50 to give 59, then use previous part/whole thinking to add 3 to the 57 to give 60 then add the remaining 3 to give 63.
- Pose problems that involve the use of doubles. As with single-digit problems doubling strategies are useful for certain problems. For example:
24 + 25 (25 + 25 = 50, then subtract 1)
15 + 16, 35 + 36, 24 + 26, 97 + 103, 402 + 398
- Pose the double-digit subtractions problems, for example:
Eva has $45. She buys a top for $29. How much does she have left?
- Discuss the ideas that the students have for solving this problem. Record the strategies on your class chart. These might include:
- Take away 20 from the 45 to leave 25. Another 9 needs to be removed. Remove the 5 to leave 20, then remove 4 more to give an answer of 16.
- Take away 20 from the 45 to leave 25. Another 9 needs to be removed. Remove 9 from a 10 frame to leave 1. There is another 10 and a 5 to add to 1 to give 16.
- Take away 30 from the 45 to leave 15. But taking away 30 is 1 too many. So add 1 to 15 to give 16.
- Pose problems for the students to work on.
47 – 28, 50 – 27, 100 – 68, 91 – 12, 63 – 23, 42 – 38, 103 – 6, 103 – 98, 81 – 34,
200 - 188
- Make the following extension problem available for students who are ready to move on. This encourages students to add and subtract more than 2 numbers in which there are smart ways to do them. Begin by discussing the following problem:
Extension One: Harry adds up the number of lunches his class orders in the week. By pairing up some of the numbers Harry quickly noticed the total lunches sold for the week was 60. How did Harry work this answer out so quickly?
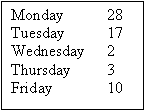
(Pairing the 28 with the 2 gives 30. Pairing the 17 with the 3 gives 20: 30 + 20 + 10 = 50.)
Extension Two: Molly has $56 when she goes shopping. She buys a CD for $28 and a pair of shoes for $26. To work out how much money she has left over she writes down 56 - 28 - 26. (Write this expression on the board. Her friend Kate sees this and almost immediately says Molly has $2 left. How did Kate do this so quickly?
- 56 - 26 = 30, 30 - 28 = 2
- 28 + 26 = 54 (from 27 + 27) and 56-54 =2
- Revisit students not working on the extension problem. Affirm their strategies and scaffold their thinking. Gather together as a class. Ask students to work in small groups to find "clever" ways to work out the following problems:
198 + 65 + 2 345 - 99 - 245 88 + 45 + 12 + 55
100 - 34 - 66 9 + 456 + 191 7 + 25 + 33 + 25
Reflecting
Refer back to the class chart. Add any new strategies and have students explain which strategies they feel the most confident using, find the easiest, find the hardest, feel they could teach another student about etc. You could also have students create posters explaining and modelling the use of each strategy.
Dear families and whānau
At school this week we have explored strategies for working out the answers to addition and subtraction problems.
Mental Magic for Experts
Ngaire knows a number of ways to work out 19 + 38
- Her first way is 20 + 40 = 60. Now 20 is one more than 19 and 40 is 2 more than 38 so take away 3 from 60 to leave 57.
- Her second way is to remove add 10 and 30 to give 40, then add 9 and 8 to give 17 then add 40 and 17 to give 57.
- Her third way is to remove 2 from the 19 to leave 17, then add this 2 to the 38 to give 40 then add and 7 to give 14 then add 17 and 40 to give 57
Write stories to show two different ways to work out the following problems. Make sure that both stories produce the same answer.
58 + 27
Story One:
Story Two:
81 - 19
Story One:
Story Two: