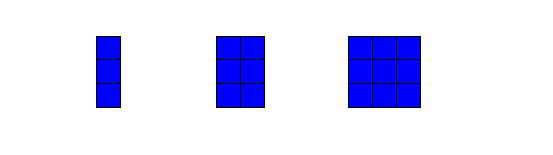
Building as a General Rule
In this unit we are paying close attention to the general rule of a pattern for the first time. We look at odd and even numbers as well as multiples of small numbers. We also look at squares and cubes of numbers and see that it is possible to make more than one pattern from the same three initial terms.
- Continue a pattern.
- Use a table of values.
- Be able to find the general rule for simple patterns.
Patterns are an important part of mathematics. They are one of the over-riding themes of the subject. It is always valuable to be able to tell the relation between two things in order to predict what will happen and understand how they inter-relate.
Patterns also provide an introduction to algebra proper as the rules for simple patterns can be first discovered in words and then be written using algebraic notation. The main rule that we concentrate on here is the general rule, though the recurrence rule is needed in the later tasks.
The general rule tells us about the value of any number of the pattern. So for the pattern 2, 4, 6, 8, … the general rule is twice the number of the term. In this unit, we concentrate on patterns with a relatively simple general rule. This is usually a multiple of a number or the power (square or cube) of a number.
Links to Numeracy
This unit provides an opportunity develop student knowledge in the area of factors, multiples and divisibility rules.
Where number patterns involve multiples of numbers this can be used to develop knowledge of basic facts, in particular factors, multiples and divisibility rules.
What is the biggest number you can think of to fit this pattern?
How do you know it will fit?
Will the number 156 be in this sequence?(or other number as appropriate)
Why / Why not?
How could you check which of these numbers fits the pattern?
What is the same about all the numbers in this sequence?
Can you see an easy way to check whether numbers will be in this sequence?
- Copymasters One, Two, Three, Four, Five, Six, Seven and Eight
- Squares of coloured paper
- (Magnetic) tiles
Getting started
We start off with an activity that should be straightforward for most students. Then we look at another where the pattern is clear but may be harder to state precisely in words. In addition to getting the students to put the patterns into words here we also look at some basic properties of even and odd numbers. These properties are that any even number plus any even number is even; any odd number plus any odd number is even; and any even number plus any odd number is odd.
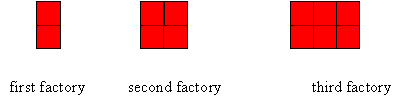
- Build the red ‘factories’ in the diagram (see also Copymaster 1) below using square pieces of paper or magnetic tiles on a whiteboard.
- Ask questions such as the following:
How many red squares do we need for the first red factory? The second? The third?
How many red squares will we need for the tenth factory? The hundredth? The 124th?
What can you say about the number of squares that you will need for any factory in this sequence? (They’re always even. ) - Explain what is meant by the general rule for a pattern. That it’s the way of finding the number associated with a given term. So that if you know the term of the sequence you can find the number associated with that term. For instance, if we knew the general rule for the factory pattern above, we could find the number of squares that the sixth factory, say, has or the tenth factory, or whatever factory number we liked.
What do you think the general rule for the pattern for these red factories is? (Twice the number of the term. )
Can we test this out with a few examples? Does it work for the first factory? The second factory? The tenth factory? - While we’re looking at this pattern, what happens if we put two of the red factories together?
Let’s experiment. Put the second and third factories together.
What do we get? What is the significance of the 5 here?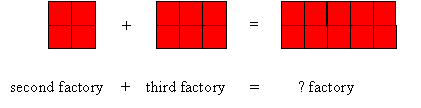
- If we add any red factory to any red factory will we always get another red factory?
Experiment some more to see if this is true or not.
If it is what is the number of the answer factory? How can you find out? - What does this tell you about adding an even number to another even number?
EVEN + EVEN = EVEN
- Now I want you to look at these green factories (see Copymaster 2). Answer as many of the questions as you can. (The general rule here is twice the number of the term before plus 1. )
- When they have had an appropriate length of time on that task, get them together to answer questions similar to those below. First emphasise the general rule. (Here you have to double the number of the term and subtract one. This pattern is clearly the odd numbers but it may not be easy to say what the general rule is in words. ) Second emphasise the fact that even + even = even, odd + odd = even and even + odd = odd. Show using the red and green factories how this comes about.
Exploring
The students now work at various stations continuing different number patterns. The patterns explored here are powers of a number and the ‘figurate’ numbers (such as the square numbers, the pentagonal numbers and the hexagonal numbers.
The station work will take about three days. On each day get the whole class together at an appropriate time to discuss the results of their work. Check that they have been able to answer all of the questions correctly and understand what they have been doing.
You may need to remind students that if they are stuck then a good way to proceed is to make a table. Place special emphasis on the general rule that exists in each pattern. Tell them to be careful because sometimes there is more than one pattern to be found.
Day 1
The material for these stations is on Copymasters 3 and 4.The students should answer the questions posed on the Copymasters. These two stations explore the shape numbers, where the shapes are the square and the pentagon.
In this piece of work, pay special attention to the ability to put the general rule into words. This shouldn’t be too difficult. In the first case the numbers are 4, 8, 12, 16, … and so the general rule is four times the number of the term. In the second case the numbers are 5, 10, 15, 20, … and so the general rule is five times the number of the term.
Day 2
The material for these stations is on Copymasters 5 and 6. The children should answer various questions posed on the Copymasters.
On the first of these Copymasters we have another shape number - this time the hexagon. So the numbers are 6, 12, 18, 24. The general rule is that the pattern number is 6 times the term number.
On the second of these Copymasters we look at a pattern that is increasing by a multiple that is a fraction. Here the numbers are 8, 12, 18, 27, 81/2, … The general rule is to multiply the previous term number by 3/2. However, this pattern can be continued another way. The students could get 8, 12, 18, 26, … Here the numbers are increasing by 4, 6, 8, … So in this case it is easier to look at the recurrence rule. Finding the general rule is quite hard.
Day 3
The material for these stations is on Copymasters 7 and 8. Again the students complete questions that are on the Copymasters.
Here again concentrate on the general rule. In these patterns, there are at least two rules that they may find here. One is easier to tackle using the general rule and the other is easier with the recurrence rule. Encourage them to find both rules. However, they may find it hard to describe the second of these rules.
In Copymaster 7 the patterns are 1, 2, 4, 8, 16, … and 1, 2, 4, 7, 11, … The first pattern is the powers of 2 (general rule: the number of the pattern is 2 raised to the power of the term minus one). In the second pattern the difference between consecutive terms is the pattern 1, 2, 3, 4, … The increase between two terms is whole number of the first of the two terms (the recurrence rule).
In Copymaster 8 the patterns are 1, 3, 9, 27, 81, … and 1, 3, 9, 19, 33, … The first pattern is the powers of 3 (general rule: the number of the pattern is 3 raised to the power of the term minus one). In the second pattern the difference between consecutive terms is the pattern 2, 6, 10, 14, … The increase between two terms starts at 2 and increases by 4 more between each consecutive pair of terms (the recurrence rule). This second rule is much harder to describe.
Reflecting
On the final day let the class make up their own building patterns. They should concentrate on making one building pattern that has a simple general rule (like the shape patterns) and one building that has two possible patterns. They should give either the general rule or the recurrence rule, whichever is the simplest.
Bring the class together and discuss some of the patterns that they have made. Concentrate on the general rule for those patterns. Try to get all of the students to put the general rule into words. Ask them to do that.
This week we have been looking at patterns to do with multiples of numbers. We have looked at the general rule and the recurrence rule for patterns. The general rule is a rule that gives you the number of squares in a building given the number of the building in the sequence. The recurrence rule tells you how to go from the number of squares in one building to the number of squares in the next.
Ask your student if he or she can continue the pattern below. Say what the general rule and the recurrence rule are. Can you work it out together?