Getting Started

1. Fold a circle in half and cut pieces out of it in any way you like. Ask the students to anticipate the pattern that the opened-up shape might have. Write down any mathematical vocabulary that might arise, in particular, terms like symmetry, or reflection. Open the cut circle to confirm the students’ predictions. The shape has reflective or line symmetry along the fold line. 
   
   What pattern can you see in the shape?
   How did the way we made the shape affect the symmetry it has?
   You may want to show how the whole shape is visible if the mirror is located along the fold line. 
   Mirror symmetry and fold symmetry have the same meaning with 2-dimensional shapes.
2. Ask: Why is reflective symmetry sometimes called mirror symmetry, fold symmetry, and flip symmetry?
   It is important for students to see that one half of the shape maps onto the other half by folding and flipping actions. Each alternative term can be demonstrated. Holding a mirror along the fold line enables students to see an image of the whole shape even when one half is masked. Similarly, the amended (cut) circle can be refolded in half and traced around. Then flip the paper over the fold line and trace around it again. The traced figure will be that of the whole amended circle.
3. Ask students to make their own shape by folding a circle in half and cutting out pieces (they must not cut all the way along the fold line). This will enable them to conjecture that all such shapes have at least one line of reflective symmetry (some may have two depending on the cuts). The symmetric shapes may be displayed on a chart.
4. Move onto folding a circle into quarters (in half then in half again) and cutting pieces out. 
   
   Before opening up the circle ask:
   What pattern do you expect the shape to have?
5. Confirm that the two fold lines are lines of reflective symmetry.
   Is there another type of pattern in this shape?
   Students may not recognise that the cutout shape has rotational symmetry as well. Trace around the shape on a whiteboard. Turn the shape one half turn (180⁰) to show that the shape maps onto itself.
   The shape has half turn symmetry. How many times will it map onto itself in a full turn?
   Students should predict order 2 rotational symmetry. That means the shape maps onto itself twice, in a full turn.
6. Ask students to create their own pattern using quarter folds of a circle. Ask them to compare their shape with that of a partner. 
   How are the shapes the same? How are they different?
   Do both shapes have the same symmetry?
   Most students will realise that there are two lines of reflective symmetry (the fold lines) but the half turn rotational symmetry is harder to spot.
7. Ask your students to anticipate then investigate what symmetry the circle shape will have if folded in eighths or sixths before cutting. Sixths can be created by folding the circle in half and then looping the half into thirds (see diagram below). (The circle folded into eighths will have at least four lines of reflection symmetry and rotational symmetry of order 4; with sixths the symmetry is six lines and order 3). Ask the students if they can see a pattern in the "least number" of lines and orders.
   
    
8. Challenge the students to use paper circles to create a shape that has rotational symmetry of order 3 but no lines of reflective symmetry. Next ask them to produce a shape that has rotational symmetry of order 4 but with no lines of reflective symmetry. Then ask for a shape that has rotational symmetry of order 5 with no lines of reflective symmetry, etc.

Session Two: Car logos

1. Begin by showing a short film clip of a car from a popular brand.
   What make of car was that?
   How do you know?
2. Investigate the logos found on motor vehicles by looking at cars in the school car park, magazine advertisements or images from the internet. PowerPoint 1 provides some common car logos. Car advertisements in magazines can also be cut out and used. Most manufacturers use symmetry of some kind in designing their logos. For example, Audi uses four intersecting circles in a line. This pattern has one line of reflection symmetry. This logo is created by translating (shifting) one circle three times.
   
3. Discuss the symmetry of each logo and compile a list of car manufacturing companies for future reference. (You may need to omit the manufacturer’s name from some of the logos to get any symmetry. For instance, removing ‘Ford’ from its logo gives an elliptical shape that has two lines of symmetry.) It is just as important to identify logos that are non-examples of symmetry. For example, the logos for Volvo and Jaguar, and Peugeot have no symmetry, even when the company name is removed.
   
4. Provide the students with drawing instruments such as rulers, protractors, drawing compasses, or jar lids, and tell them to recreate the car logos they saw in the car park, online or in magazines. Have the images available for them to refer to, if needed. At times it may be necessary to bring the class together to discuss construction skills. For example, for a logo involving rotational symmetry of order 3, a protractor will be useful. Since there are 360° in a full turn, one third of that is 120°, which gives the angle measured at the centre for dividing a circle in thirds. Construction skills like drawing a right angle by using a protractor or compass construction may be modelled if necessary.

Session Three: Logos in the media

1. As homework (see Homelink) ask the students to find other examples of logos. Obviously not all logos have symmetry. Sporting goods manufacturers are good examples of this. Nike uses a “swish” that was designed to embody movement. Adidas uses three stripes etc. Examples will illustrate to the students that logos have to be both aesthetically pleasing (i.e. often symmetric) and suggestive of the nature of the company. Share the logos students bring along and group them by symmetry discussing what message is suggested by the logo image. This has strong links to visual language in the English curriculum. For example, the Canterbury Clothing Company has a logo of three translating, overlapping C’s with a kiwi inside them that give the impression of a single ball moving from left to right.
   
2. Set up a matrix for classifying the logos. Create a chart by pasting logos in the appropriate cell. The Canterbury logo belongs in the bottom right cell as it has no reflective or rotational symmetry. It does have translation symmetry.
   
   The Starbucks logo belongs in the bottom left cell as it has reflective symmetry but no rotational symmetry.

3. Set up the following scenario for the students: 
   You work for an advertising company as a logo designer. There are five new companies that need new logos. They have stipulated that the logo must have some symmetry but must also suggest what goods and services they provide. (If you wish, they may also be required to come up with a slogan that captures the message, e.g. "Just do it".)
   Here are the companies:
   • Sweeties - a company that makes sugar-free lollies that taste great and don’t ruin people’s teeth.
   • Gadgets - who make neat construction gadgets (gears, blocks, wheels, etc.), so people can create their own toys.
   • Mana - an after-school club that supports students in learning te reo Māori.
   • Duds - makers of cool clothes especially for primary school children.
   • Hapori māra - a community organisation that specialises in planting native trees
   • Brainbuilders - the people who provide one-on-one tutoring service for students. You get one-on-one help so you are in a class of your own!
4. Give the students sufficient time to design logos for one or more of the companies. They will need to present the logo in a short report to each company that shows what symmetries are involved and how the design suggests the goods or services the company provides. You may decide to set up a voting system for the class to decide on a winning logo for each company. 

Session Four

1. Provide your students with paper copies of logos (Copymaster 1). Display the logos and ask the students to collaborate (mahi tahi) with a partner and write down the symmetry that each design has (this is useful for assessment purposes). Get pairs to have a korero about what they have written with another pair group, then bring the class together for a collective discussion.
2. For each logo get students to demonstrate what symmetry the design has by using a mirror, or folding and flipping, and by tracing and rotating. Make a list of symmetries for each design.
3. Tell the students to look at their first list and add any information they may have missed. If they do this in a new colour you will have evidence of their initial independent understanding and their new shared understanding.
4. If time permits explore how a simple graphic programme, like PowerPoint, can be used to create simple design elements. By copying the element, reflecting or rotating it, then grouping elements together, complex symmetric design can be created.

Session 1

1. Talk to the students about buildings and how they are constructed. Give them images of buildings to inspire them and for them to discuss. You could also ask a local builder who is a member of your community to come and talk to your class about construction.
   What material is used to construct buildings? (wood, bricks, mortar, sand, cement, etc.)
   How do builders put a house together?
   How do they build walls?
    
2. Get the students to describe the brick pattern on walls. Show them Copymaster 1, or another picture of a brick wall. Talk about the features of the pattern (i.e. there are no gaps, the bricks are in rows, each row is slightly displaced from the row below.)
   Why do you want to have no gaps in a wall?
   (You might note that some walls do have gaps. Why?)
    
3. Are there any other ways of using bricks to build a wall?
    
4. Get the students to produce their own (2-dimensional) bricks. The bricks should be rectangles that are twice as long as they are wide. This can be done using graph paper and then tracing round one to produce many. Model this process for the class. They could also draw a number of bricks on graph paper to be photocopied, before cutting up the photocopied bricks. Copymaster 2 can be photocopied if you would prefer students not to make their own bricks.
    
5. Ask the students to create a wall using the bricks that they have just produced. They might copy the pattern shown in Copymaster 1 or arrange the bricks in any pattern they like. However, if they think up their own patterns there are two rules that must be followed: (i) there are to be no gaps and (ii) the pattern must be capable of being continued indefinitely (to cover a very big wall!). Draw attention back to the brick wall example shown previously, and highlight each of these features.

6. Roam and work with the students. If needed, they could work in pairs or small groups. Once they have one brick pattern, see if they can find others. Emphasise that the bricks don’t always have to be ‘horizontal’ and that the pattern doesn’t have to be practical. It’s OK if the pattern won’t produce a very strong wall.

   

7. Bring the class together and let the students discuss the patterns that they have made. The students should be able to identify that their patterns have no gaps and that they can go on forever in all directions. Support them with their explanations as necessary. 
8. Tell the class that they have been making tessellations. A tessellation is a way of using a fixed shape to cover the whole area of a flat surface (a plane). Tessellations have two important properties: (i) they have no gaps (all of the plane is covered) and (ii) they go on forever (no matter where you go in the plane the shapes will still be covering the part of the plane that you can see. Sometimes we call a tessellation a tiling. Record a summary of these key points on a class chart.

Session 2: Regular Polygons

In this session the students will explore tessellations by regular polygons. The key finding is that regular polygons don’t tessellate. If you haven’t got any solid regular polygons handy then they can be made using Copymaster 3, or displayed digitally.

1. Ask the students to recap the work of the last lesson. They can share their ideas with a buddy, small group or the whole class.
   What did we do in the last lesson?
   What shapes did we use?
   What word did we learn? (tessellation or maybe tiling)
   How many rules does a tessellation have? What are they?
   Display the class chart constructed in the last session, and revise any key points that students didn’t emphasise in discussion.
    
2. Today we are going to look at special types of shapes called regular polygons. 
    
3. Show the students a variety of relevant artworks and images that feature tessellations (this could be an opportunity to look at a local tapa cloth or kowhaiwhai panel). Ask them to identify any regular polygons. Emphasise that a regular polygon has sides that are equal and interior angles that are equal. 

4. What we want to do is to see which of these shapes tessellate and which don’t. We’ll then construct this table together.

   Shape	Tessellate?	Why?
   equilateral triangle	yes
   square
   regular pentagon
   regular hexagon
   regular heptagon
   regular octagon
   regular nonagon
   regular decagon
   regular hendecagon	no
   regular dodecagon

5. Distribute the regular polygons to students and ask them to find out which shapes tessellate and which don’t. Let the students tackle the problem in any way that they like. As you go round their groups check that they understand that there are to be no gaps and that the patterns must continue forever in all directions. Check too, that if they can’t find a tessellation, they can explain why one doesn’t exist. (It isn’t good enough to say that they have tried for 5 minutes and they can’t find one. They need to be able to justify why there have to be gaps or why the pattern can’t go on forever. It should usually be the first reason. This is fortunate, as it is easier to justify.) They could record the findings from their investigations on a large sheet of paper - on which they could draw each tessellation and write a few sentences explaining why it does or does not tessellate. Encourage the students to refer back to the class chart constructed in session 1 for a reminder of the ‘rules’ tessellations must follow.
    
6. Groups who finish early could be asked to see if they could find some different tessellations using a combination of the regular polygons, or using the regular polygons they have not yet investigated.

7. Bring the class together to discuss their results. After each group has reported and justified their claims add them to the table. A completed form of the table is given below. The angles talked about in the third column are the interior angles of the polygons. If your students are confident in measuring angles, they could measure the angles of the shapes they investigated and add this information to their charts. Otherwise, briefly model the measurement of the angles in a few shapes, and explain how the total sum of the angles is found (i.e. add them together). If your students are not familiar with measuring angles, and you feel this knowledge will be too much in addition to the learning in this unit, you could use the existence of gaps in the pattern of shapes to justify whether the shape does or does not tessellate

   Shape	Tessellate?	Why?
   equilateral triangle	yes	show pattern; 6 x 60° = 360° so they fit.
   square	yes	show pattern; 4 x 90° = 360° so they fit.
   regular pentagon	no	no multiple of 108° makes 360° nor do multiples of 108° plus 180° .
   regular hexagon	yes	show pattern; 3 x 120° = 360° so they fit.
   regular heptagon	no	no multiple of 128.57° makes 360° nor do multiples of 128.57° plus 180° .
   regular octagon	no	no multiple of 135° makes 360° nor do multiples of 135° plus 180° .
   regular nonagon	no	no multiple of 140° makes 360° nor do multiples of 140° plus 180° .
   regular decagon	no	no multiple of 144° makes 360° nor do multiples of 144° plus 180° .
   regular hendecagon	no	no multiple of 147.27° makes 360° nor do multiples of 147.27° plus 180° .
   regular dodecagon	no	no multiple of 150° makes 360° nor do multiples of 150° plus 180° .

8. Ask the class if they have any new information or conjectures (i.e. statements that have not yet been proven as correct or incorrect) about tilings by regular polygons that could be added to the class chart.

Session 3: Quadrilaterals

In this session the students try to extend their results about regular polygons to more general polygons. The key findings are that regular polygons don’t tessellate and all quadrilaterals tessellate.

1. Get the class to recall what happened in the last session. The key points are (a) what is a tessellation; (b) tessellations were found for only three types of regular polygons; and (c) which types? The key points are (a) what is a tessellation; (b) tessellations were found for only three types of regular polygons; and (c) which types? Display the class chart and highlight any information which students did not identify.
    
2. Ask "which shapes do we now know will tessellate?" (The three regular polygons and the rectangle – from the brick patterns.) We know that two kinds of 4-sided figures will tessellate. What other types of quadrilaterals will tessellate?
    
3. Provide the students with various quadrilaterals (see Copymaster 4) and let them experiment. A table can again be constructed like the one in Session 1.
    
4. Give the students the opportunity to experiment for themselves with other quadrilaterals. (For instance the students who finish quickly and can justify what they have done should go on to inventing quadrilateral tilings of their own.) Ask them to record their findings on the chart they constructed in the previous session. Remind them that there are two things that can be varied – the lengths of the sides and the sizes of the interior angles. Suggest that they vary the interior angles first. If your students are not familiar with measuring angles, ask them to look at the lengths of the sides, and whether any gaps are formed when they try to tessellate the new shapes.
    
5. Let the students report back on what they found. What new information did they discover? What conjecture do they have about tessellations by quadrilaterals? Can they justify that conjecture?

Teaching Notes:
The students will discover that any quadrilateral will tessellate. Because the interior angles of any quadrilateral add up to 360° , we need to put four figures together at a point so that each one of the four (possibly) different angles is used. In this pattern, sides of equal length also have to fit together. The pattern below shows how to do this.

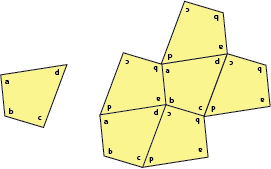
We have shown that we can fit four of these polygons together at a vertex without gaps. How can we be sure that we can continue the pattern indefinitely? You can see that the pattern in the figure is made up of a wiggly strip of quadrilaterals. In this strip, one quadrilateral is placed one way and then it’s placed another. These wiggly strips can put side by side forever. What you see in the drawing is what you would see anywhere in the plane.

Notice that it doesn’t matter whether the quadrilateral is convex (no interior angles bigger than 180° ), as above, or concave, as below.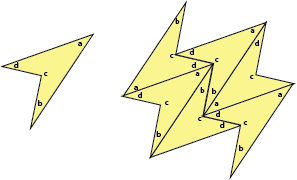

Session 4: Triangles.

If all quadrilaterals tessellate is the same true for all triangles? Repeat the last session but this time use triangles. Provide students with a range of triangles to experiment with (e.g. scalene, equilateral, isosceles, right-angle, obtuse, acute). Briefly introduce the names of the triangles you include, and if appropriate, make reference to the types of angles they demonstrate.

Teaching Notes:
It is easier to establish whether or not triangles tessellate. Since the interior angles of a triangle add up to 180° , we need to make sure that each angle is represented at a point. In the diagram below, the angles form a continuous, straight line. This means that we can put the triangles together to make a row. We can fit two such rows together. In fact we can fit as many rows together as we like until the entire plane is covered.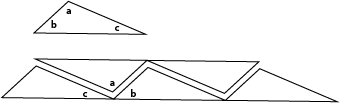

Session 5: Pentagons

Review the facts: all triangles tessellate; and all quadrilaterals tessellate. What do we know about regular polygons? (They don’t tessellate.) Does that mean that no pentagon tessellates? Ask the students to experiment using the pentagons from Copymaster 5 and by inventing their own pentagonal shapes. What results can you find?

If the students can’t find any pentagonal tessellations, you might remind them how they constructed the triangular and quadrilateral tessellations. Rows were very important. So it might be an idea to try to use rows in some way to try to form pentagonal tilings.

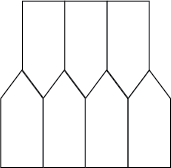
The situation with pentagons is more complicated than with either triangles or quadrilaterals. Some pentagons do tessellate and some do not. From the evidence of the regular pentagon, it is unlikely that all the interior angles of a pentagon could cluster around a similar point in a similar way. That means that there have to be at least two types of points where pentagons come together. So we have to distribute the sizes of the interior angles so that this can happen. This enables us to get tilings like the one below.

Session 6: Reflecting

1. Discuss with the class the results of the last few days. Refer back to the charts constructed and record some summary statements.
   What have you discovered?
   What is a tessellation?
   What polygons do you know that tessellate?
   What polygons definitely do not tessellate?
2. Now we know that all triangles tessellate, all quadrilaterals tessellate and that regular hexagons tessellate.
   What questions do you think that we ought to ask now? (Do you think that all hexagons tessellate? What do you think? Why?)
3. Experiment for yourselves. Make your own hexagonal shapes and come up with a conjecture.
4. After they have tried this for a while, get them to report back on their conclusions.
5. Revisit their conjecture about regular tessellations. How could you prove this?

Teaching Notes:
There are other hexagons apart from regular hexagons that do tessellate, such as the concave hexagon shown below.

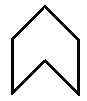
If we can arrange the angles of a hexagon in such a way that no combination of them will add up to 360° (or 180°), then it won’t be possible for that hexagon to tessellate.

The conjecture that only regular polygons that tessellate are the equilateral triangle, the square, and the hexagon is proved in Fitness, Level 4.

Getting Started

We begin our exploration of tessellating art by altering squares and parallelograms.

1. Show the students the altered square tessellation (Copymaster 1).
   
   What can you tell me about this tessellation?
   Why is it a tessellation?
   Which of the regular tessellations does it look like it has been made from?
   Can you see how this tessellation has been made? Show us.

2. Look at the tessellating shape and predict how it was altered.

   

3. Give each student a square cardboard tile. Ask them to cut a piece out of one side of the square. Attach the cut out piece to the opposite side of the square with cellotape.
   Will your new shape tessellate? Try it and see.
4. Have the students trace their new shapes several times onto blank sheets of paper to see if the altered shape tessellates.
5. Discuss.
   Is your altered shape symmetric? What type of symmetry does it have?
   Does the new shape have to be symmetric to tessellate?
   (Note: When altering a square by translating opposite sides to form a new tessellating figure, the alteration does not have to be symmetrical.)
   Describe the movement of the shape as you tessellate with it? (translation or shifting)
6. Ask students to repeat the altering process with other quadrilaterals that tessellate, for example, parallelograms and rectangles. Also include "wonky" (scalene) quadrilaterals. Not all alterations will create tessellating shapes and this is a useful discovery. The key to creating tessellating shapes is altering opposite sides in exactly the same way.
7. Allow time to share and discuss at the end of the session.
   What did you discover about altering shapes to create new shapes that also tessellate?
   Why do you think it is possible to alter shapes in this way and still end up with a shape that tessellates?
   Did you create any shapes that do not tessellate? Why do you think that they won’t tessellate?

Exploring

Over the next 2-3 sessions we use our imaginations to create interesting art pieces using altered tessellating shapes.

1. Begin by looking at one of the shapes created yesterday.

2. Brainstorm for ideas about what the shape could be. In the following shape the addition of an "eye" creates a fish-like shape.

   

3. Have the students select a shape to use for the basis of a piece of tessellating art.
4. After they have decided on a shape, have them trace it across a piece of paper to create a tessellation. To transform it into an Escher style piece let them put details on each of the shapes.
5. Search online for “Creating Escher Tessellations”. Many useful videos exist to show your students how other transformations can be used to alter a ‘parent polygon.’ Useful transformations include rotation of half a side about the midpoint, and rotation of a whole side onto another. You may decide to introduce these more complex transformations gradually so students master one process before beginning another. There are also free online tools available for creating Escher tessellations.
6. Ask questions as the students work that focus on the symmetries of the shape and the tessellation.
   Tell me about the symmetries of your shape? (reflection symmetry, rotational symmetry)
   How are you generating the tessellation? (translating? rotating? reflecting?)
   Why does your shape tessellate? (Encourage the students to focus on the fact that the sum of the angles at any point must equal 360 degrees)
7. Ask the students to make a written record about the process that they used to make the tessellating shape and the tessellation.
8. At the end of each session share the tessellating art.

Reflecting

In this final session we analyse tessellations and attempt to predict the processes that were used to create them.

1. Begin by looking at the bumpy squares tessellation (Copymaster 2).
   What shape do you think has been altered?
   How do you think it was altered?
2. Next we distribute our tessellating art, created in the previous days, to see if others can determine the tessellating shape and the process by which the tessellation was formed.
3. We check with the artists to see if we predicted correctly.