Students explore basic concepts, language and reasoning relating to chance and data.
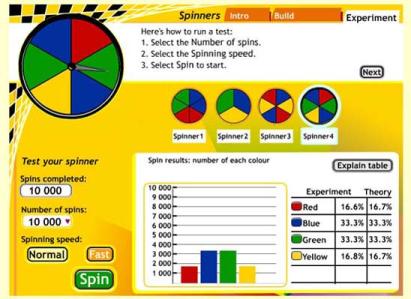
Students construct spinners to investigate and test the relationship between the structure of a random generator (sample space) and the likelihood of individual outcomes or results from a series of outcomes. The rapid generation of data in dynamic tables and graphs allows an introduction to the notion of long-run data being more reliable than short-run data.
Spinners: explore
The student starts with an equal spinner of three different colours. Before starting a trial the student must observe the sample space of the spinner and make a prediction as to the most likely outcomes of the result of the trial. The student then runs a trial of 1000 spins only. A dynamic graph changes to reflect outcomes of the trials. A miniature of the spinner and graph are retained as a record.
The student alters sizes of sectors and initiates another series of trials, with results shown on a graph. A miniature of the spinner and graph is retained as a record. This is repeated with a third spinner.
The student is presented with six labels to consider, then matches the most appropriate label to each of the three spinners, e.g. 'Same chance for each colour', 'Red will spin more often than other colours', 'Less chance for yellow'.
Mathematical focus is on awareness of equal likelihood, less likely, more likely, and exploring the relationship between sample space and likelihood of outcomes. Data emphasis is on the result of each spin and introduces the notion of long run data being more informative about likelihood.