Trains
Rename improper fractions as mixed numbers and position improper fractions on a number line.
Number Framework Stage 6
Background Maths
Many students have difficulty appreciating that fractions can be both operators and numbers. Early experiences often reinforce the idea of fractions as operators, for example, finding one-half of 16 or three quarters of 12. Experiences with treating fractions as numbers are equally important for the development of decimal understanding later.
For example, the students need to know that one-half is a number located between zero and one. Activities that focus on locating fractions between and equal to whole numbers help to establish the place of fractions as numbers. It is important that the students have experiences that require interpretation of a fraction in relation to a changing one (whole).
Using Materials
Problem: “Suppose that I make a train from these rods. (Hold up the orange rod.)How long do you think a train of three carriages would be? Use you hands to show me?” “If this orange rod is a full carriage, how big is this rod?” (Hold up a yellow rod). The students should say it’s half a carriage because two of them make a whole carriage.
Ask, “How many half carriages would I need to make three whole carriages?”
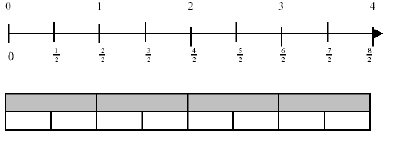
Record the answer as “six half carriages make three whole carriages”.
Ask how this could be written using numerals. (6 x1/2 = 6/2 = 3)
“Suppose that you could make up whole carriages with these rods.” (red)
“What fraction of a carriage is each rod? (one-fifth) How do you know?” (Five of them make a whole carriage.)
“Suppose you had 12 of these one-fifth carriages. How many whole carriages could you make?”
Ask the students how they could record this using numerals or words.
“Twelve-fifths is the same as two wholes and two-fifths (12/5 = 2 2/5).”
Give the students other experiences that involve modelling with the materials. For example:
Redefine the dark green rods as the whole carriages of a different railway.“Red rods will be one-third of a carriage, and light green rods will be one-half.”
“How many whole carriages could you make with 18 one-third carriages?” (18 x 1/3 = 18/3 = 6)
“How many whole carriages could you make with seven one-half carriages?” (7 x 1/2 = 7/2 = 3 1/2 )
Record these results using a number line by putting the rods end-onend to establish the correct position of numbers. For example:
Using Imaging
Predicting: Pose problems for the students to solve where they must anticipate the answer by imaging. For example:
Choose the dark blue rod to be the length of one carriage. The light green rod will be one-third of a carriage.
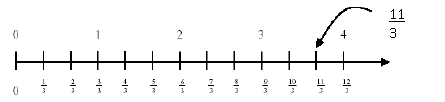
Ask, “If you had 11 one-third carriages, how many whole carriages would you have?” Place the rods alongside each other to help the students to visualise the answer.
Draw number lines and write equations to record the results
Other examples might be:
Define a brown rod as one carriage.
“How many carriages can you make with nine red rods?” (quarters)
“How many carriages can you make with 17 crimson rods?” (halves)
Using Number Properties
The students solve problems involving renaming improper fractions (numerator larger than the denominator) as mixed numbers (whole numbers and fractions), e.g., 9/4= 2 1/4. Pose problems that are difficult to visualise so that the students are required to attend to the numbers. For example: “Rename these fractions as mixed numbers:
14/3 = 4 2/3 , 15/4 = 3 3/4 , 28/7 = 4, 46/10 = 4 6/10 , 75/100
(Note the last fraction is less than one so it can only be renamed as 3/4.)
Recording
Students can record their answers as equations and on number lines.