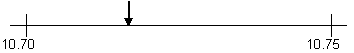Rounding Numbers
In this unit students will identify why it is important to round numbers sensibly. They will practise accurately and sensibly rounding in a range of different contexts.
- Sensibly round whole numbers in context.
- Sensibly round decimal numbers.
Structure
Each of the sessions in this unit begins with a whole class introduction to a rounding context or problem, and where appropriate, an opportunity for whole class revision of learning from the previous session. Following this, students are provided with one or more tasks, related to the just-introduced context, to complete. As students work, roam and observe their capacity for working with the numbers and key mathematical concepts. Use these observations to inform your planning for future teaching sessions. Conclude each session with discussion, modelled problems, and opportunities for students to share their working and mathematical ideas.
Rounding
In this unit, students engage with the concepts of 'rounding' and 'significant figures'. The process of rounding a number means replacing the numeral by another numeral that has fewer significant figures. The decision whether to round up or down is made in relation to the value of the leading digit being rounded off. The convention is that 0, 1, 2, 3, and 4 are effectively just chopped off (truncated) while 5, 6, 7, 8, and 9 are truncated but the first digit not truncated is increased by a value of one.
In the context of measuring to the nearest millimetre, this means measurements recorded as 52.365, 12.764, 4.986, 2.031, and 5.699 (in metres) could be changed to measurements to the nearest centimetre (that is, to two decimal places (2dp)). These would be recorded as 52.37, 12.76, 4.99, 2.03, and 5.70.
Significant Figures
Significant figures (or significant digits) assess the accuracy of the numeral as an expression of the real value of the number that it represents. This is important as numerals are often expressed as approximate values. When a number is given in decimal notation, the error should not exceed a half unit of the last digit retained.
Therefore, if a number has been rounded to 1400, we would expect that, before it was rounded to the nearest whole number, it was greater than or equal to 1399.5 and less than 1400.5 It should be no more than 0.5 different due to the rounding. In this example we can say that the four figures are reliable, and that the number has been expressed to four significant figures.
If we had been rounding to the nearest 100, then 1379 would also be written as 1400. However, in this case, only the first two digits would be significant. We would then expect that the true value was greater than or equal to 1350 and less than 1449.
It is easy to see the number of significant figures in a numeral that has been written in standard form. In the examples above, the first example of 1400 (to four significant figures) should be written as 1.400 x 103, whilst the second example of 1400 (to two significant figures) should be written as 1.4 x 103.
The learning opportunities in this unit can be differentiated by providing or removing support to students, and by varying the task requirements. Ways to differentiate include:
- asking students to round smaller, simpler numbers, before progressing to the rounding of larger, more complex numbers.
- encouraging students to use number lines and diagrams to justify and model their thinking
- providing opportunities for students to work in a range of flexible groupings to encourage peer learning, scaffolding, and extension
- varying the number of independent/paired tasks students are expected to complete within a session
- constructing a class chart of key ideas, models, and expressions to be used by students as a point of reference
- modelling and providing explicit teaching around rounding with a range of numbers. Gradually releasing your level of responsibility allows you to scaffold students towards working independently
- allowing the use of calculators for making predictions and confirming calculations, and to ease the mental load associated with calculation.
A variety of contexts are reflected in the tasks included in this unit. These contexts might be supplemented by, or adapted to, better reflect students' interests, cultural backgrounds, or to make connections to learning from other curriculum areas. Examples might include local populations, budgets and profits related to local businesses, and distances and quantities related to your local environment. Consider how these adaptations might make links to your students' interests, cultural backgrounds, to learning from other curriculum areas, and to current events.
Te reo Māori kupu such as whakaawhiwhi (round), tau ā-ira (decimal number), and tauoti (whole number) could be introduced in this unit and used throughout other mathematical learning.
- Number lines
- Calculators
- Access to internet
Session 1
This session provides students with multiple opportunities to explore the rounding of decimals and whole numbers.
Introduce students to the context of rounding numbers for newspaper headlines. Tell students that the government of Outer Australia reported spending $33,883,641.31 in the 2002-2003 financial year. As a class, find out how much the New Zealand government spent in the previous financial year. Discuss how to put this number into a newspaper headline. A sensible answer here is "Government spends X-amount (e.g. $34 million) last year".
While many students will round the 8 hundred thousand ‘up’ because it is over ‘5’ it is desirable to present this as a number line and see which end the number is closer to.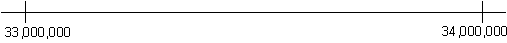
Discuss why this line has 33,500,000 in the middle and why 33,883,641.31 is roughly where the arrow is.
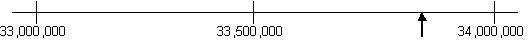
As an extended opportunity, your students could research the amounts spent by different countries in the previous financial year, round these sensibly, and use the figure to write a newspaper headline.
- Provide students with time to complete one or more of the following tasks.
- Round these numbers suitably for use in newspaper headlines:
- Quality Stores make a profit of $3,493,631.
- Prime Minister paid $251,419.91 last year.
- Scientist estimates there are 56,409,100 possums in New Zealand.
- Cost of producing cheese drops to 101.8 cents per kilogram due to improved efficiency at the cheese factory.
- A milk factory reports it bought 27,309,604 litres of milk from farmers last year.
- 7 plates are to be sold for $75. The price of 1 plate is 75 ÷ 7 = $10.71428571. Discuss how to round to get these different answers:
- The supermarket charges to the nearest cent so one plate is priced at $10.71.
- The petrol station does not use cents only multiples of 5 cents. So it charges $10.70
Number lines are very useful.Supermarket:
Petrol Station:
- Complete the table below.
As an extension, students could create their own table using items for the hypothetical cost of food for a party, a weekly lunch budget, cost of a food basket etc. Utilise a context that is relevant and engaging for your students.
| Cost per Item | |||||
| Items | Total Cost | Number | Calculator | Supermarket | Petrol Station |
| Plates | $75.00 | 7 | 10.71428571 | $10.71 | $10.70 |
| Tins of Soup | $49.40 | 13 | |||
| Cola cans | $104.10 | 97 | |||
| Frozen Peas | $71.11 | 21 | |||
| Fly Spray | $811.00 | 206 | |||
| Chocolate bars | $111.00 | 73 | |||
Session 2
This session provides students with further opportunities to explore the rounding of decimal numbers.
- Revise the learning from yesterday. You might create a list of the key concepts students remember, have students present their learning, or have students complete a rounding task independently, before sharing their work with a pair. Note and address any misconceptions.
- Pose the following problem to students:
Jerry measures the width of the school football field and finds it is 70.4m wide. Discuss why this means the true width is between 70.35m and 70.45m. Melissa measures the length of the field and finds it is 101.8m long. Discuss why it is between 101.75m and 101.85m long. Jerry and Melissa now collaborate to find the area by using the calculator. Unfortunately 70.4 x 101.8 = 7166.75 is not a sensible answer.
- Discuss why this is overly accurate given the possible errors in the data.
- Discuss why 70.35 x 101.75 < True Area < 70.45 x 101.85 that is 7158.1125 m2< True Area < 7175.3325m2. Rounding the lower and upper areas to 3 significant figures is a sensible answer but rounding to 2 decimal places (7166.75) is not. In practice an answer like 7170m2 is good enough for practical problems like how much grass seed is needed to resow the field.
- Provide students with time to complete the following task in appropriate groupings. Roam and provide support.
- Complete the table for area of rectangles.
| Length | Width | Area | ||||||
| Lower | Measured | Upper | Lower | Measured | Upper | Lowest | Rounded | Highest |
| 101.75 | 101.8 | 101.85 | 70.35 | 70.4 | 70.45 | 7158.1125 | 7170 | 7175.3325 |
| 111.7 | 61.3 | |||||||
| 88.7 | 9.81 | |||||||
| 202 | 11.62 | |||||||
| 181.7 | 161.7 | |||||||
| 9.31 | 6.34 | |||||||
| 1.61 | 0.86 | |||||||
- Discuss why, when multiplying numbers from measurements the answer is never more accurate that the lowest number of significant figures in the factors.
- The area of a rectangle is 100.4m and has one side of 20.4m. So the other side is 100.4 ÷ 20.4 = 4.92156862m.
- Discuss why the exact answer is between 100.35 ÷ 20.45 and 100.45 ÷ 20.35 that is 4.907m and 4.936m.
- Discuss why 4.9m is a sensible answer.
Session 3
This session explores the question how many significant figures are there in a number?
- Revise the learning from yesterday. You might create a list of the key concepts students remember, have students present their learning, or have students complete a rounding task independently, before sharing their work with a pair. Note and address any misconceptions.
- Explain to students: At the Olympics the running track is 400m long. If this number has 1 significant figure the length of the track is between 350 and 450. Why is this not a sensible estimate?
- Discuss and fill in the table
| Length | Number of Sig. Figs. | Least possible length | Largest possible length | Sensible |
| 400m | 1 | 350 | 450 | No |
| 400m | 2 | 395 | 405 | No |
| 400m | 3 | 399.5 | ||
| 400m | 4 | 399.95 | ||
| 400m | 5 |
So a 400m running track is laid out to an accuracy of 5 significant figures or perhaps 6.
- Provide students with time to complete the following task in appropriate groupings. Roam and provide support.
Rounding distances
- Julie says she is about 50 metres from home. How many significant figures are in this number?
- A building plan shows the length of a room is 6700mm long. How many significant figures?
Rounding larger whole and decimal numbers
- The Lotto people predict a first division prize of $1,400,000. How many significant figures?
- The census shows New Zealand population is 4 270 000. How many significant figures?
- A supermarket works out its prices to be to the nearest cent. Suppose a kilogram of chicken costs $14.91. Discuss why it is more sensible to say this number has been rounded to 2 decimal places rather than 4 significant figures.
Applying trigonometry
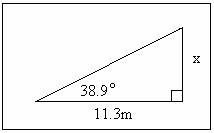
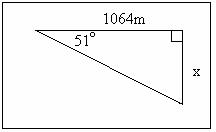
If trigonometry has been studied, discuss calculated lengths need to be rounded sensibly. For example;
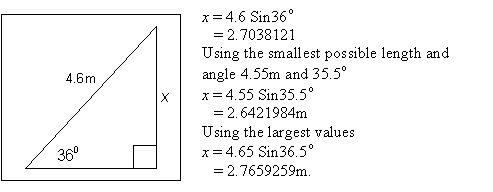
- Discuss why a sensible answer for x is between 2.6 and 2.8. So 2.7 is reasonable.
Find reasonable answers for x.
Session 4
This session explores the rounding of decimal numbers with number lines.
Pose the following question to students:
The choices for rounding 16.469 to 1 decimal place are either 16.4 or 16.5. Which is most suitable?
- Discuss why the middle is 16.45 and fill in ten divisions and add the arrow for 16.469.
![]()
- Discuss why 16.469 is rounded to 16.5 and not 16.4.
- Provide students with time to complete the following task in appropriate groupings. Roam and provide support.
Students who have a limited understanding of decimal place value often find dividing a scale into 10 and labelling each division difficult. Draw number lines divided into ten labelled parts to solve these problems.
|
|
|
|
|
|
- Pose the following true story to students:
Mr. Brown rounded 14.486 to the nearest whole number by rounding 14.486 to 14.49 by the "over 5" rule. Then he rounded 14.49 to 14.5 by the same rule. Then he rounded 14.5 to 15 by the rule. Unfortunately this is wrong.
Discuss why.
This highlights the danger of the rule versus realising that the number is rounded to the closer of the left hand end or right hand end on a number line.
Dear families and whānau,
Recently we have been exploring how to round decimals and whole numbers sensibly and accurately. With your child this week, find some examples of decimals or large (e.g. over 100 00) whole numbers in your local environment. Ask your child to teach you how to round these numbers sensibly.