Investigating Integers
This unit begins with Freudenthal’s (1983) annihilation model for demonstrating the addition and subtraction of integers then goes on to introduce other representations. It is designed for students who are able to choose appropriately from a broad range of mental strategies to estimate answers and efficiently solve addition and subtraction problems.
- Solve simple addition and subtraction equations involving integers.
This unit of work is useful for students working at stage 7 of the Number Framework, Advanced Multiplicative. Students at this stage select from a broad range of strategies to solve addition problems with decimals, and are adept at subdividing and recombining numbers to simplify problems.
Although students at this stage will be very familiar with the number line as a model for addition and subtraction, this unit does not promote the use of the number line, as it is considered problematic as a model to show subtraction of negative numbers.
The key teaching points covered in this unit are:
- An integer is a whole number that can be either greater than 0, called positive, or less than 0, called negative.
- Zero is neither positive nor negative.
- Two integers that are the same distance from the origin in opposite directions are called opposites and when added cancel each other out making 0.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- using physical materials, as suggested in the unit, to represent positive and negative values
- linking the addition and subtraction of integers to patterns formed from the addition and subtraction of whole numbers
- using calculators in anticipatory ways, e.g. to predict and then check a result
- contextualising integers in situations that are meaningful to students, (e.g. around possessing and owing money).
The context for this unit is purely mathematical. Ideas are developed using different coloured objects to represent the concept of positive and negative one. Integers can be applied to a range of everyday contexts that might make the mathematics more accessible to students. Useful contexts include possessing and owing money (whole numbers of dollars), height above and below sea level, scores in sports games like golf, and temperatures.
Te reo Māori kupu such as tau tōpū (integers), tāpiri (add, addition), and tango (subtract, subtraction) could be introduced in this unit and used throughout other mathematical learning.
- Copymasters Money Matters, Close to Zero, Bonuses and Penalties, and Integer Quick Draw
- Counters of two colours (e.g. black and red)
Getting started
Begin with a true/false conjecture on board for students to discuss. Ask students:
Do you think the statement is true or false and why? 1 – -4 = 5
- Ask students to discuss their ideas with a partner. Listen for student explanations. Discuss the idea of positive and negative numbers; introduce the term integer if it does not arise in the discussion.
An integer is a whole number that can be either greater than 0, called positive, or less than 0, called negative. Zero is neither positive nor negative - Ask students to explain what is happening in the equation 1 – -4 = 5. Ask how this equation could be demonstrated with equipment.
- Use the counters of two different colours (e.g. black and red). Explain to students that black counters represent positive and red counters represent negative - show the number 2 as 2 black counters.
- Ask:
What would happen if I added, three more black and three red?
What would I have now?
Make sure students understand that the extra three black and three red cancel each other out, so the answer is still 2.
Two integers (e.g. 3 and -3) that are the same distance from the origin (e.g. 2) in opposite directions are called opposites and when added cancel each other out making 0. - Use black and red pen to record the expressions you have modelled on the board: 2 + 3 = 5 and 5 + -3 = 2. Draw attention to the addition of -3.
- Ask students, in pairs, to generate some expressions similar to the one you modelled. These expressions should: be one-step, only use the operations addition and subtraction; and demonstrate how, when added, two integers (e.g. 3 and -3) that are the same distance from the origin (e.g. 2) in opposite directions, cancel each other out making 0. Students should use red and black counters to model their equations, before writing each expression. If time allows, students could also use digital tools, other materials, or physical movement to model their thinking.
- Support students as necessary. Look for students to recognise that they can use ny number of extra red and black counters, so long as these sets are equivalent.
- Pose an equation for students to model with equipment:
3 – 4 =
- Discuss the answer and how they used the equipment to model it.
- Repeat this process with the following:
-3 + 2 =
4 – -1 =
- 5 + -2 = - Ask students to make up three more problems for their to swap with their partner to solve. These could also be discussed, and the solutions justified, for the class. Support small groups and individual students as necessary, making sure to use materials to model the addition and subtraction of integers.
- Pose another true/false conjecture for discussion.
-3 – 2 = -1
- Conclude the session by asking students to record or discuss what they have noticed about adding and subtracting integers. Compile a summary of these ideas in a chart or modelling book.
Exploring
Over the next few days introduce the students to a selection of other models and contexts for addition and subtraction of integers, choosing from the list below. Students could, if they wished, use the double coloured counters to model some of the calculations. As they work through tasks, add any new ideas to the modelling book or chart. Pay attention to gaps in students’ knowledge, and take the opportunity of students working independently to take small-group or individualised teaching sessions that address these gaps. Ensure you model and explain how to use each of the following activities.
- Integer learning experiences from Book 5: Teaching Addition, Subtraction and Place Value
- Money Matters (copymaster) - Discuss the idea of cash and debts, this task could be followed up with the Figure It Out lesson Money Matters, p21, Number Year 7/8, Book 4.
- Close to Zero game (copymaster).
- Bonuses and Penalties game (copymaster) after playing the game get students to make up some of their own cards.
- Integer Quick Draw game (copymaster).
Reflecting
- Pose a variety of True/False conjectures using slightly more complex numbers, like those in the expressions below, framed in a context that is engaging and meaningful to your students (e.g. culturally or environmentally significant, relevant to current learning interests or learning from other curriculum areas).
3 – -12 = -15
4 - 16 = 20
3 + -17= 20
7 - 13= -6 - Revisit the summary of ideas where students have recorded what they have noticed about adding and subtracting integers. Ask students to work with a partner to develop some guidelines related to adding and subtracting integers for another classroom, for example adding a negative number is just like…, subtracting a negative number is like… This could be done on paper or in another format (e.g. video, digital presentation, acting it out, using other physical manipulatives or diagrams).
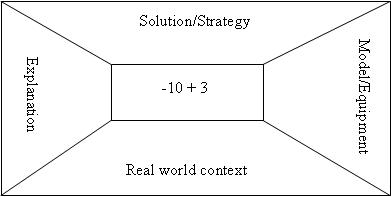
Alternatively, you could introduce Alistair McIntosh’s thinkboard. Model completing the sections with the equation given below. Ask students to make up an equation (or provide them with one) and write it in the middle of the thinkboard. They should complete each section of the model. You could run this as a ‘carousel’ activity, in which different (random) groups of students receive a question. After giving students time, in their groups, to work out the answer to the question and fill in their thinkboards, make new groups composed of a student from each original group. Every student in the new group should share their group’s ‘thinkboard’ with their new group. This gives all students a chance to listen to each other, explain their thinking, and see different examples of integers being used in real-world contexts
Dear family and whānau,
This week we have been investigating positive and negative integers. Your child will be bringing home a game to share with you as a way to practise adding and subtracting integers. If they get stuck they will be able to use a diagram of cancelling out to solve the problem. Have fun!