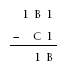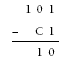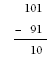Darting for Cover
These are level 3 number and statistics problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (420 KB)
use addition facts to solve problems (Problem 1)
use subtraction facts and place value knowledge to solve problems (Problem 2)
find outcomes using a systematic approach (Problems 3 and 4)
Problem One
Making an organised list is a useful strategy for finding all the possible outcomes.
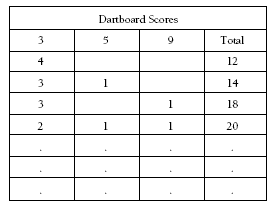
All the possibilities with at least one dart landing on 3
3 + 3 + 3 + 3 = 12
3 + 3 + 3 + 5 = 14
3 + 3 + 3 + 9 = 18
3 + 3 + 5 + 5 = 16
3 + 3 + 5 + 9 = 20
3 + 3 + 9 + 9 = 24
3 + 5 + 5 + 5 = 18
3 + 5 + 5 + 9 = 22
3 + 5 + 9 + 9 = 26
3 + 9 + 9 + 9 = 30
All the remaining possibilities with at least one dart landing on 5 and no darts on 3
5 + 5 + 5 + 5 = 20
5 + 5 + 5 + 9 = 24
5 + 5 + 9 + 9 = 28
5 + 9 + 9 + 9 = 32
The only possibility involving all the darts on 9 with none on 3 or 5
9 + 9 + 9 + 9 = 36
These results could also be organised into a table to avoid duplications:
Problem Two
This example belongs to a family of letter-for-number problems called cryptorithms.
A useful strategy in these problems is to put the letters and all the possible digits in a table so that possibilities can be eliminated.
Considering the A in the hundreds place of the top number, it is clear that this must stand for one because there is no hundreds digit in the answer.
This transforms the problem into:
From this, we can use the ones column to see that B must be zero.
So the problem becomes:
This then shows us that C must be nine because 10 – C = 1.
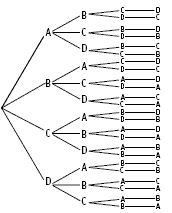
Problem Three
Students may enjoy acting the problem out by forming groups of four and trying out various orders.
Another strategy is to solve a simpler problem. Starting with two people, A and B, there are two possible orders:
AB BA
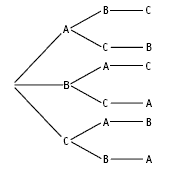
With three people, A, B, and C, there are six possible orders:
ABC ACB BAC BCA CAB CBA
Note how the possibilities with A in front are exhausted, then all the possibilities with B in front, and then with C in front.
Students are unlikely to realise that the pattern involves multiplication unless these orders are organised as a tree diagram:
3 x 2 x 1 = 6 (called 3! or three factorial)
When another person is added, the tree diagram becomes:
4 x 3 x 2 x 1 = 24 (called 4! or four factorial)
The solution for the possible orders of five people is given by 5 x 4 x 3 x 2 x 1 = 120 (or 5!).
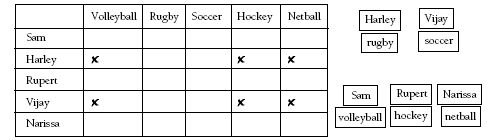
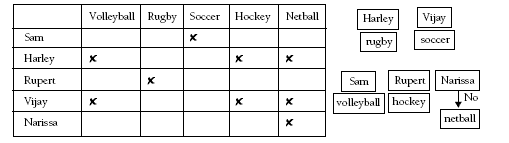
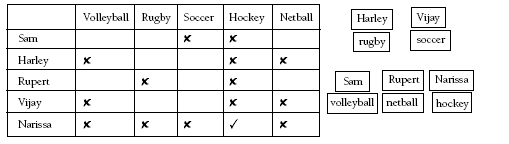
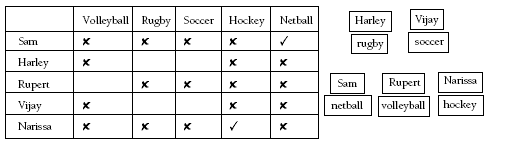
Problem Four
These types of logic problems can be modelled with a table or by using moveable labels of the people and sports. Using these models, the problem can be solved like this:
In Vijay’s and Harley’s favourite sports, all the players can kick the ball.
No one’s favourite sport begins with the same letter as their name.
Narissa likes the sport where the ball is hit with a stick.
Sam loves being the goal shoot in her sport.
Both Harley’s and Sam’s favourite sports are played with a spherical ball.
Answers to Problems
1. Shape a
2. 50
3.
4. 11 red, 7 blue, 17 yellow, and 2 green