Getting Started
The purpose of this session is to explore the range of strategies already used by students to solve addition and subtraction problems. This lesson will enable you to evaluate which strategies need to be focused on in greater depth. In turn, you will identify students in your group as "expert" in particular strategies. There are two problems given as examples for exploration. You may want to use further examples of your own. Consider adapting the contexts used in these problems to further engage your students.
- Problem 1: Sarah has $288 in the bank. She then deposits her pay for $127 from her part time job at a cafe. How much does she have now?
Ask the students to work out the answer in their heads or by recording in some way. Give the students plenty of thinking and recording time. Ask the students to share their solutions and how they solved the problem with a peer. The following are possible responses:
Place value (mentally, possibly with the support of equations on an empty number line):
288 + 127 is just like 288 + 100 +20 +7. So that’s 388… 408… 415.
Tidy numbers (mentally, possibly with the support of equations on an empty number line):
If I tidy 288 to 300 it would be easier. To do that I need to add 12 to 288, which means I have to take 12 off the 127. So that’s 300 plus 115.
Algorithm (usually written):
Students may visualise or record a written algorithm like this:
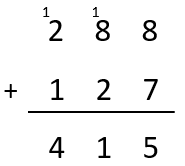
Understanding is revealed by the language used to describe the strategy, such as, “8 plus 7 equals 15. I wrote 5 in the ones place and carried the extra ten into the tens place because 15 is made up of 5 and 10 and I can only record one digit in the ones place.”
As different strategies arise ask the students to explain why they chose to solve the problem in that way. Accept all the correct strategies that are elicited, recording the strategies to reflect upon later in the unit on the class T chart (under the addition heading). You might also ask students to model how their strategies work with place value materials. Note that folding back to justify a strategy is often more difficult than performing the strategy.
- Problem 2 Sarah has $466 in her bank account and spends $178 on a concert ticket. How much money does she have left in her bank account?
Ask students to solve the problem mentally, giving them plenty of thinking and recording time. Then ask students to share their solutions and how they solved the problem with a peer. Possible responses are:
Reversibility (adding on to find the difference with recording to ease memory load):
$466 - $178 is the same as saying how much do you need to add to $178 to get $466. $178 plus $22 makes $200, plus $200 more makes $400 plus $66 makes $466. If you add up $22 plus $200 plus $66 you get $288.
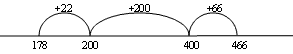
Subtracting a tidy number then compensating
$466 - $200 = $266. I took off $200 instead of $178 so I need to ‘pay back’ $22. $266 + $22 = $288.
Equal additions:
You round the $178 to $200 by adding $22. $466 - $200 is $266. Then you put on $22 to keep the difference the same, so it’s $288.
Algorithm (usually written):
Students may visualise or record a written algorithm like this:
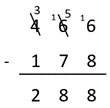
Understanding is revealed by the language used to describe the strategy, such as, “6 minus 8 doesn’t work (ignoring integers) so I changed one ten from the tens column into ones to make 16. I wrote 16 in the ones place and took one ten off in the tens place…”
As different strategies arise, ask the students to explain why they chose to solve the problem in that way. Accept all the correct strategies that are elicited, and justified, recording the strategies to reflect upon later in the unit (under the ‘subtraction’ heading on the class T chart). You might also ask students to model how their strategies work with place value materials. Note that folding back to justify a strategy is often more difficult than performing the strategy.
Subtraction strategies tend to be more difficult to control than addition strategies, given comparable numbers. Look out for students compensating the wrong way (taking more off) in the tidy number strategy and making errors when using the algorithm.
Use your observations to plan for your subsequent teaching from the exploring section outlined below.
Exploring
Over the next two to three days, explore different strategies for addition and subtraction of whole numbers. Give the strategies a name so students can tell others which strategy they are preferencing for a given problem. Highlight when certain strategies are most efficient, for example, In the problem 357 + 189 tidy numbers would be a useful strategy because 189 is close to 200.
Follow a similar lesson structure each day to the introductory session, with students sharing their solutions to the initial questions and discussing why these questions lend themselves to the strategy being explicitly taught. Conclude each session by asking students to make statements about when the strategy would be most useful and why the certain problem is appropriate, e.g., tidy numbers when one number is close to 100 or 1000, standard place value (hundreds, tens, and ones) when no renaming is needed and reversibility when neither of the other two numbers are easy for subtraction. It is important to record examples of strategies as they will be used for reflection at the end of the unit. Some strategies may require more teaching time, greater use of materials, and more scaffolded and individualised teaching. Ensure that students who demonstrate proficiency with the strategies early on in each session have adequate opportunities for practice, extension, and supporting their peers (if appropriate).
The questions provided are intended as examples for the promotion of the identified strategies. If the students are not secure with a strategy you may need to make up some of your own questions to address student needs. Consider adapting the contexts reflected in these problems to further engage your students.
Tidy numbers then compensating
- Room 9 are selling muesli bars at lunchtime to raise money for their camp. They had 434 at the beginning of lunchtime and sold 179, how many did they have left to sell?
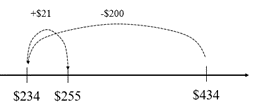
The tidy numbers strategy involves rounding a number in a question to make the question easier to solve. In the above question, 179 can be rounded to either 180 (by adding 1), or 200 (by adding 21). If 200 is subtracted (434 – 200 = 234) then the result is 21 less than the answer. 234 + 21 = 255. An empty number line shows this strategy clearly:
For addition questions, one addend can be tidied by taking from the other addend. Alternatively, both addends might be tidied, and compensation used to adjust for the tidying. - The following questions can be used to elicit discussion about the strategy.
- What tidy number could you use that is close to one of the numbers in the problem?
- What do you need to do to the other number if you tidy up this number? Why?
- Why is this strategy useful for this problem?
- What knowledge helps you to solve a problem like this?
- If the students do not understand the tidy numbers concept, use place value equipment (place value blocks, place value people, beaNZ) and/or an empty number line to model the problems physically. Students should be encouraged to record equations and number lines to track their thinking and reduce load on working memory.
- Use the following questions for further practice if required:
- Ariana has scored 739 runs for her cricket club this season. Last season she scored 294, how many did she score in total in the last two seasons?
Shifting six between the addends gives 739 + 294 = 733 + 300 = 1033. - Nigel sold his guitar for $587 and his amp for $395. How much money did he make from both sales?
Rounding 587 to 600 and 395 to 400, then compensating gives 587 + 395 = 600 + 400 – 13 – 5 = $982. - Farmer Samsoni has 1623 sheep, and he sells 898 sheep at the local sale. How many sheep does he have left?
Rounding 898 to 900 gives 1623 – 898 = 1623 – 900 + 2 = 725 - Other examples might be:
568 + 392
661 - 393
1287 + 589
1432 - 596
- Note that the problems posed here are using a tidying up strategy rather than tidying down i.e. 103 down to 100 as in these situations place value tends to be a more useful strategy.
Place Value (written algorithm)
- For the community hangi, 356 potatoes are peeled and there are 233 left to be peeled. How many potatoes will there be altogether?
The place value strategy involves adding the ones, tens, hundreds, and so on. In the above problem:
300 + 200 is added
Then 50 + 30
And finally 6 + 3
As an algorithm the calculation is represented as:
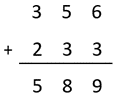
- The following questions can be used to elicit discussion about the strategy:
- How can you use your knowledge of place value to solve this problem?
- Why is this strategy useful for this problem?
- If the students do not understand the strategy, use place value equipment to show the problems physically. Students will find it useful to record and keep track of their thinking .
- Use the following questions for further practice if required:
- Zac has $498 available on his eftpos card and spends $243 on a new BMX bike, how much money does he have left?
- Other problems might be:
3221 + 348
4886 - 1654
613 + 372
784 – 473
Reversibility (adding one rather than subtracting to find the difference)
- Faloa is helping his Mum build a path. There were 438 bricks in the pile and they used 169 of them yesterday. How many bricks have they got left to lay today?
The reversibility strategy involves turning a subtraction problem into an addition one so the problem above becomes:
169 + ? = 438
Using tidy numbers to solve the problem makes calculation easier:
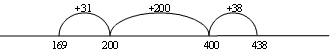
Or
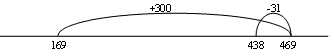
- The following questions can be used to elicit discussion about the strategy:
- How could we think of this as an addition equation?
- What do you need to add to make it easier to solve?
- How can you keep track of how much you have added altogether?
- Why is this strategy useful for this problem?
- What knowledge helps you to solve a problem like this?
- If the students do not understand the concept, use a number line to show the problems graphically. Students will find it useful to record and keep track of their thinking using a number line.
- Use the following questions for further practice if required:
- At the mail sorting office there were 547 letters to be sorted, 268 of these were distributed to private boxes, how many were left to be delivered?
- The school library has a total collection of 1034 books and 459 are issued at the moment, how many are on the shelves?
- Other problems might be:
628 - 342
537 - 261
742 - 353
1521 - 754
1762 - 968
1656 - 867
Reflecting
As a conclusion to the week’s work, give the students the following five problems to solve. Pose the problems in contexts that are relevant and engaging for your students. Ask students to discuss, with a peer or in small groups, which strategy they think will be most useful for each problem and justify their view. For some problems many strategies may be equally efficient. After students have solved the problems, engage in discussion about the effectiveness of their selected strategies.
Some students may have a favourite strategy that they use, sometimes to the exclusion of all others. The best approach is to pose problems where the preferred strategy may not be the most efficient. For example, 289 + 748 is most suited to using tidy numbers and compensation.
Problems for discussion
1318 - 747
763 - 194
433 + 452
1993 + 639
4729 - 1318
You might also like to also try some problems with more than two numbers in them, such as:
721 – 373 - 89
663 - 61 - 88
63 + 422 + 49
42 + 781 + 121
84 + 343 - 89
- Discuss the different strategies explored during the week and ask students to explain in their own words what types of problem each strategy would be useful for solving, and what types of problem each strategy would not be useful for solving. Ask the students to draw a strategy ‘from a hat’ and write questions specific to that strategy for a partner.
- Conclude the unit by showing the students the questions asked in the initial session again. Discuss whether they would solve the problems in a different way now, and how their thinking has evolved. With a partner, students could create a short presentation demonstrating how they would solve one addition and one subtraction problem, naming the strategies used, and justifying the use of their chosen strategies.
Close to 100
Recall the number of tens and hundreds in 100s and 1000s.
Identify symbols for any fraction, including tenths, hundredths, thousandths, and those greater than 1.
Solve addition and subtraction problems using decomposition, leading to a written algorithm
Number Framework Stages 5 and 6
Dice
Each player rules up a column for “tens” and a column for “ones”. The aim of the game is to get a total as close to 100 as possible. The student tosses a dice and decides whether the number will be put in the ones or the tens place. For example, if a four is thrown, it could either be 40 or four. The dice is rolled a total of seven times. All seven numbers must be used. The total of all the columned numbers may exceed 100, but the students will need to decide which player has got closer to 100.
Extension Activity
Use larger numbers and decimals for the target numbers. Vary the number of throws and what the thrown number can represent, such as:
Closest to 1 000: 10 throws of hundreds, tens, or ones.
Closest to 10: 10 throws of ones, tenths, or hundredths.
Closest to 1: 10 throws of tenths, hundredths, or thousandths
Make 1000
In this unit the students form collections of 1000 objects. In doing this they examine the relationship between 1000 and smaller numbers, specifically 100 and 10.
As part of the work in this unit, the students will get to appreciate the size of 1000. It will take them some time to collect and display 1000 objects. In the process they will realise that 1000 is a reasonably large number. The size aspect of number is an important one. We need to have a ‘feel’ for how big numbers are so that we can appreciate everyday things such as how far it is to another town, how heavy things are or how much they cost.
In an effort to display their 1000 objects so that they are readily counted, the students will be encouraged to bundle the objects into groups of 10 and 100. This will help them see the relevance of the decimal counting system and the relationship between the numbers 10, 100 and 1000. A knowledge of the decimal system is fundamental to working with number, especially where the four operations of arithmetic are concerned. The advantage of this system over previous ones, such as that used by the Romans, is its efficiency in counting and calculating. This is all due to the fact that the system is based on the powers of ten – 101 = 10, 102 = 100, 103 = 1000...
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
The activities in this can be adapted to make them more interesting for your students by adding contexts that are familiar to them. Each student can already choose their own collection to make with a partner, but you may like to make the example collection be something more meaningful to your students, for example shells if you are near the beach, or small pebbles from a local stream.
Getting Started
We begin our unit by making guesses about the number of beans in jars. We then work in pairs to decide how we are going to make a collection of a 1000 items.
I want you to think about how many beans might be in each of these jars. You can look closely at each jar but you can’t tip the beans out and count them. At the end of the week we will check your guesses.
How many do you think are in the jar? Why do you think that?
Which jar was the easiest to work out? Why? Have you seen that many before? Where?
Can we write it any other ways?
Discuss the ideas that the students have about 1000.
Tell me how you think you can collect 1000 of those?
Where are you going to collect them? (home, school, friends)
How will you display them?
Will your collection cost very much?
Do you need help with your collection? What?
Exploring
Over the next 2 to 3 days the students work with their partners to collect, make, count and display their collection of a 1000 objects.
How many objects have you collected?
How are you keeping track?
How many more do you need to collect?
Will you get to 1000 by Friday? How do you know?
How are you going to display your collection? Why are you doing it that way?
Will the others in the class be able to work out that you have a 1000 without having to count each object?
Reflecting
In today’s session we create a 1000-block using multilink cubes. We do this by building it from sticks with 10 cubes.
Are there enough sticks here for 1000 cubes? Look at the collection of 10 sticks.
Are there enough sticks here for 1000 cubes?
How do you know?
How could we find out?
Ask the students to make collections of 100 with the 10-sticks.
Look at the 100’s collections. (As a class develop a name for the 10x10 cubes, for example; walls, panels.) Look at the 100's collections.( As a class develop a name for the 10x10 cubes, for example; walls, panels.)
Do we have a 100?
How many 100s do we need? How do you know?
How many 10s do we have in 1000? How do you know?
Dear family and whānau,
At school this week we have worked with a partner to make a collection of one thousand objects. We have explored ways of displaying our objects so that we can tell that we have a 1000 without having to count every one. You are very welcome to come to our classroom to look at our 1000 collections.
1000 letters
At home this week we want your child to find a collection of 1000 letters of the alphabet from a page of the newspaper. Encourage your child to explain how they are grouping the letters so that they keep track of their counting.
Figure it Out Links
Some links from the Figure It Out series which you may find useful are:
Compatible Numbers
Solve addition problems by using compatible numbers.
Number Framework Stage 5.
Using Materials
Problem: Tina has 6 tomatoes, Miriam has 2 tomatoes and Liam has 3 tomatoes. They use 9 tomatoes for a salad. How many tomatoes are left?
Discuss how to record the problem then record 6 + 2 + 3 - 9 on the board. The students model piles of 6, 2 and 3 counters. Discuss which two piles make 9 and remove them to leave 2. Record 2 on the board.
Examples: Word stories and recording for: 5 + 2 + 5 – 10, 9 + 5 +1 – 6, 8 + 2 + 7 – 9, 4 + 5 – 9, 3 + 5 + 5 – 8, 4 + 6 + 4 + 3 - 7….
Using Imaging
Examples: Word stories and recording for: 4 + 2 + 5 – 9, 8 + 5 + 2 – 7, 10 + 2 + 7 - 12, 10 + 5 – 15, 3 + 2 + 6 – 5, 2 + 6 + 4 + 3 - 7
Using Number Properties
Examples. Write these numbers on paper and cross out pairs and the numbers subtracted to get the answers: 8 + 6 + 4 – 10, 7 + 8 + 2 – 9, 7+ 3 + 3 + 7 - 10 – 10, 1 + 2 + 5 + 2 - 7 – 3, 9 + 6 + 4 - 7 - 2 ….
Addition and subtraction on the number line
Change start-unknown problems to change-unknown problems.
Solve addition and subtraction problems by compensating with tidy numbers.
Number Framework Stage 5
Number Lines (Material Master 5-12)
Students need to develop an understanding of place-value mental strategies by using equipment that allows for grouping as well as a continuous model such as a number line. The number line model preserves the magnitude of a number and shows where it fits among other numbers. It also provides a strong image for students to work with and is particularly useful for solving subtraction problems.
Addition and subtraction on a number line involve keeping the first number whole and partitioning the second. For example, 56 + 37 = ? can be solved in the following way:
Likewise, on a number line, 83 – 24 = ? can be shown as:
Step 1: 83 – 20 = 63
Step 2: 63 – 4 = 59
Alternatively:
Step 1: 83 – 3 = 80
Step 2: 80 – 20 = 60
Step 3: 60 – 1 = 59
Using materials
Problem: On sports day, there were fifty-seven senior students and forty-five junior students competing in different events. How many students were competing altogether at the sports day?
Have the students solve the problem by using empty number lines.
Ask: “How might you show this problem on a number line?” Record strategies on the board or in the modelling book.
Examples: Word problems and recording for: 68 + 26, 37 + 24, 158 + 46, 72 – 34, 143 – 26, 251 – 33 …
Using imaging
Students rely on the number line image to support their thinking.
Examples: Word problems and recording for: 85 – 56, 78 + 27, 86 + 47, 42 – 25 …
Using number properties
Students can jot down a number to support short-term memory.
Examples: Word problems and recording for: 528 – 86, 728 + 34, 456 + 127, 563 – 125 …
Problems like 23 + ? = 71
Solve addition and subtraction problems by compensating with tidy numbers.
Number Framework Stage 5
Number Lines (Material Master 5-12)
This problem can be solved by jumping up to 30 then jumping to 71. However,because 23 is some distance from 30, another method, namely adding 50 to the 23 first, is worth learning.
Using Materials
Problem: 23 plus what is 71?
Write 23 + ? = 71 on the board. On the class number line jump 50 from 23 to reach 73. Discuss why we need to jump back 2 and so why is the answer 48. Record 23 + 48 = 71.
Examples. Record and do these problems on first side of the sheet. 24 + ? = 82, 52 + ? = 90, 25 + ? = 91, 13 + ? = 71, 12 + ? = 91, 54 + ? = 72, 45 + ? = 83, 14 + ? = 83 …
Imaging
Use imaging for those students who are struggling.
Using Number Properties
Examples. Record and do these problems on paper: 24 + ? = 82, 52 + ? = 90, 24 + ? = 91, 12 + ? = 61, 82 + ? = 101
Alien Estimates
This is a level 3 number activity from the Figure It Out series. It relates to Stage 6 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (233 KB)
make estimations for addition problems
Number Framework Links
Use this activity to:
• encourage transition from early additive part–whole strategies (stage 5) to advanced additive part–whole strategies (stage 6)
• help the students to extend their advanced additive part–whole strategies (stage 6) in the domain of addition and subtraction.
This activity encourages students to use place value knowledge and additive part–whole strategies to estimate the results of calculations.
Students need to know numbers up to the hundreds of thousands to complete this activity. They need to be familiar with rounding numbers to the closest tidy number, for example, rounding 82 145 to the nearest tidy number in the thousands would give 82 000.
Some students may have problems with place value if, for example, they don’t know that for 82 000 + 45 000, they can calculate 82 + 45 in the thousands place. Once they realise they can calculate in this way, you will need to ensure that they don’t treat as ones units the numbers in the hundreds, thousands, ten thousands places, and so on. Place Value Houses are a useful way of clarifying any misconceptions that the students may have. (See The Power of Powers, pages 14–15, in Number Sense and Algebraic Thinking: Book One, Figure It Out, Level 3.)
This activity would be useful as an independent follow-up for a group that has just focused on rounding whole numbers to the closest tidy number in the tens, hundreds, or thousands.
With a guided teaching group, set the scene by asking about the students’ favourite computer or games-machine programmes and whether they’ve ever played a multi-person computer game.
Some students may be reluctant to estimate the answers in question 1 and may want to work out the calculation exactly. Encourage them to focus on what Rongomai has explained in her speech bubble rather than starting with the boxes of scores. Ask questions such as:
Where has Rongomai got the numbers 82 and 46 from? (The 82 is really 82 000, which is Ben’s score of 82 145 rounded down to the nearest tidy number in the thousands. The 46 refers to 46 000, which is Eseta’s score of 45 877 rounded up to the nearest tidy number in the thousands.) Why do you think Rongomai decided to round the scores to the nearest thousand? (She wanted to make them into numbers she could add easily in her head, such as 82 000 + 46 000, but still be pretty accurate. If she’d rounded to the nearest tens of thousands, her estimation wouldn’t
have been as close to the actual total [80 000 + 50 000 = 130 000].)
What strategy might she have used to work out 82 + 46? How would you do it? (Rongomai could have used place value partitioning [80 + 40 = 120, 2 + 6 = 8, then 120 + 8 = 128] or added a tidy number and compensated [82 + 50 = 132, 132 – 4 = 128] or made equal adjustments [82 + 46 = 80 + 48 = 128].)
For question 2, before the students attempt to calculate the totals in round 2, ask: How would you round each person’s score if you were using Rongomai’s strategy?
For more estimating practice, the students could make up their own scores for round 3, follow the “deliberate mistake” step in question 2a ii, and swap with a classmate.
You could use questions 2b and 3 for formative assessment if the students are able to articulate the decisions they make when estimating.
Students who have difficulty rounding numbers to the nearest thousand may benefit from using an empty number line to help them visualise the distance of a number from its tidy number neighbours.
For a number like 69 034, tell the students that they’re trying to find out which tidy number in the thousands it is closest to. Start your number line at 60 000 and get the students to count by saying the number words with you as you mark 61 000, 62 000, 63 000, … up to 70 000 on it.
Then ask: Which two tidy numbers on the number line will the number 69 034 be between? (Circle 69 000 and 70 000.) These are its thousands tidy number neighbours. So which tidy number is 69 034 closest to on our number line?
Encourage the students to use imaging with questions such as:
Which thousands tidy numbers are going to be our number’s neighbours?
Which of these two tidy number neighbours is our number closest to?
The students using number properties may start talking in terms of the number of hundreds and how that will tell them that the number is closer to the next 1 000 up or to the 1 000 before.
Answers to Activity
1. Yes, Rongomai is correct. She rounded 82 145 down to 82 000 and 45 877 up to 46 000. Then she rounded 61 480 down to 61 000 and 67 952 up to 68 000. Ben had entered 1 instead of 7 on the calculator. The Martians’ round 1 score should
have been 129 432.
2. a. i. Round 2: Cyborgs 272 733, Martians 270 954
ii.–iii. Results will vary.
b. One possible strategy (Rongomai’s) is to round the numbers to the nearest 1 000
and work out what 69 000 plus 204 000 is for the Cyborgs and what 176 000 plus
95 000 is for the Martians team.
3. Estimates will vary. A sensible estimate is 300 000 + 140 000 = 440 000. Any estimate should focus on the digits in the high value places and ignore those in the lower value places.
Numeracy Project materials (see Numeracy Books page)
• Book 4: Teaching Number Knowledge
Place Value Houses (identifying multi-digit numbers up to trillions)
Swedish Rounding (rounding to the nearest 5 cents)
Sensible Rounding (according to the context of the problem)
• Book 8: Teaching Number Sense and Algebraic Thinking
Checking Addition and Subtraction by Estimation
Whole Number Rounding (rounding to the nearest 1, 10, 100, and 1000)
Rounding Decimals
Addition and Subtraction Pick n Mix
In this unit we look at a range of strategies for solving addition and subtraction problems with whole numbers. This supports students anticipating, from the structure of a problem, which strategies might be best suited to solving it.
Students at Level 3 of the New Zealand Curriculum select from a broad range of strategies to solve addition problems. This involves partitoning and recombining numbers to simplify problems and draws on students' knowledge of addition and subtraction facts, and knowledge of place value of whole numbers to at least 1000.
The key teaching point is that some problems can be easier to solve in certain ways. Teachers should elicit strategy discussion around problems to get students to justify their decisions about strategy selection in terms of the usefulness of the strategy for the problem. The following ideas support this decision making:
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
The three main types of addition and subtraction problem are applied in this unit: joining sets (addition), separating sets (subtraction), and finding differences (either addition or subtraction). Choose contexts that make links to other relevant curriculum areas, reflect the cultural backgrounds, identities and interests of your student, and might broaden students’ views of when mathematics is applied. Commonly used settings might involve money, points in sport or cultural pursuits, measurements, and collectable items. For consistency, you could choose one context in which all of the problems presented within this unit could be framed.
Te reo Māori kupu such as tāpiri (addition), tango (subtraction), and huatango (difference in subtraction) could be introduced in this unit and used throughout other mathematical learning
Getting Started
The purpose of this session is to explore the range of strategies already used by students to solve addition and subtraction problems. This lesson will enable you to evaluate which strategies need to be focused on in greater depth. In turn, you will identify students in your group as "expert" in particular strategies. There are two problems given as examples for exploration. You may want to use further examples of your own. Consider adapting the contexts used in these problems to further engage your students.
Ask the students to work out the answer in their heads or by recording in some way. Give the students plenty of thinking and recording time. Ask the students to share their solutions and how they solved the problem with a peer. The following are possible responses:
Place value (mentally, possibly with the support of equations on an empty number line):
288 + 127 is just like 288 + 100 +20 +7. So that’s 388… 408… 415.
Tidy numbers (mentally, possibly with the support of equations on an empty number line):
If I tidy 288 to 300 it would be easier. To do that I need to add 12 to 288, which means I have to take 12 off the 127. So that’s 300 plus 115.
Algorithm (usually written):
Students may visualise or record a written algorithm like this:
Understanding is revealed by the language used to describe the strategy, such as, “8 plus 7 equals 15. I wrote 5 in the ones place and carried the extra ten into the tens place because 15 is made up of 5 and 10 and I can only record one digit in the ones place.”
As different strategies arise ask the students to explain why they chose to solve the problem in that way. Accept all the correct strategies that are elicited, recording the strategies to reflect upon later in the unit on the class T chart (under the addition heading). You might also ask students to model how their strategies work with place value materials. Note that folding back to justify a strategy is often more difficult than performing the strategy.
Ask students to solve the problem mentally, giving them plenty of thinking and recording time. Then ask students to share their solutions and how they solved the problem with a peer. Possible responses are:
Reversibility (adding on to find the difference with recording to ease memory load):
$466 - $178 is the same as saying how much do you need to add to $178 to get $466. $178 plus $22 makes $200, plus $200 more makes $400 plus $66 makes $466. If you add up $22 plus $200 plus $66 you get $288.
Subtracting a tidy number then compensating
$466 - $200 = $266. I took off $200 instead of $178 so I need to ‘pay back’ $22. $266 + $22 = $288.
Equal additions:
You round the $178 to $200 by adding $22. $466 - $200 is $266. Then you put on $22 to keep the difference the same, so it’s $288.
Algorithm (usually written):
Students may visualise or record a written algorithm like this:
Understanding is revealed by the language used to describe the strategy, such as, “6 minus 8 doesn’t work (ignoring integers) so I changed one ten from the tens column into ones to make 16. I wrote 16 in the ones place and took one ten off in the tens place…”
As different strategies arise, ask the students to explain why they chose to solve the problem in that way. Accept all the correct strategies that are elicited, and justified, recording the strategies to reflect upon later in the unit (under the ‘subtraction’ heading on the class T chart). You might also ask students to model how their strategies work with place value materials. Note that folding back to justify a strategy is often more difficult than performing the strategy.
Subtraction strategies tend to be more difficult to control than addition strategies, given comparable numbers. Look out for students compensating the wrong way (taking more off) in the tidy number strategy and making errors when using the algorithm.
Use your observations to plan for your subsequent teaching from the exploring section outlined below.
Exploring
Over the next two to three days, explore different strategies for addition and subtraction of whole numbers. Give the strategies a name so students can tell others which strategy they are preferencing for a given problem. Highlight when certain strategies are most efficient, for example, In the problem 357 + 189 tidy numbers would be a useful strategy because 189 is close to 200.
Follow a similar lesson structure each day to the introductory session, with students sharing their solutions to the initial questions and discussing why these questions lend themselves to the strategy being explicitly taught. Conclude each session by asking students to make statements about when the strategy would be most useful and why the certain problem is appropriate, e.g., tidy numbers when one number is close to 100 or 1000, standard place value (hundreds, tens, and ones) when no renaming is needed and reversibility when neither of the other two numbers are easy for subtraction. It is important to record examples of strategies as they will be used for reflection at the end of the unit. Some strategies may require more teaching time, greater use of materials, and more scaffolded and individualised teaching. Ensure that students who demonstrate proficiency with the strategies early on in each session have adequate opportunities for practice, extension, and supporting their peers (if appropriate).
The questions provided are intended as examples for the promotion of the identified strategies. If the students are not secure with a strategy you may need to make up some of your own questions to address student needs. Consider adapting the contexts reflected in these problems to further engage your students.
Tidy numbers then compensating
The tidy numbers strategy involves rounding a number in a question to make the question easier to solve. In the above question, 179 can be rounded to either 180 (by adding 1), or 200 (by adding 21). If 200 is subtracted (434 – 200 = 234) then the result is 21 less than the answer. 234 + 21 = 255. An empty number line shows this strategy clearly:
For addition questions, one addend can be tidied by taking from the other addend. Alternatively, both addends might be tidied, and compensation used to adjust for the tidying.
Shifting six between the addends gives 739 + 294 = 733 + 300 = 1033.
Rounding 587 to 600 and 395 to 400, then compensating gives 587 + 395 = 600 + 400 – 13 – 5 = $982.
Rounding 898 to 900 gives 1623 – 898 = 1623 – 900 + 2 = 725
568 + 392
661 - 393
1287 + 589
1432 - 596
Place Value (written algorithm)
The place value strategy involves adding the ones, tens, hundreds, and so on. In the above problem:
300 + 200 is added
Then 50 + 30
And finally 6 + 3
As an algorithm the calculation is represented as:
3221 + 348
4886 - 1654
613 + 372
784 – 473
Reversibility (adding one rather than subtracting to find the difference)
The reversibility strategy involves turning a subtraction problem into an addition one so the problem above becomes:
169 + ? = 438
Using tidy numbers to solve the problem makes calculation easier:
Or
628 - 342
537 - 261
742 - 353
1521 - 754
1762 - 968
1656 - 867
Reflecting
As a conclusion to the week’s work, give the students the following five problems to solve. Pose the problems in contexts that are relevant and engaging for your students. Ask students to discuss, with a peer or in small groups, which strategy they think will be most useful for each problem and justify their view. For some problems many strategies may be equally efficient. After students have solved the problems, engage in discussion about the effectiveness of their selected strategies.
Some students may have a favourite strategy that they use, sometimes to the exclusion of all others. The best approach is to pose problems where the preferred strategy may not be the most efficient. For example, 289 + 748 is most suited to using tidy numbers and compensation.
Problems for discussion
1318 - 747
763 - 194
433 + 452
1993 + 639
4729 - 1318
You might also like to also try some problems with more than two numbers in them, such as:
721 – 373 - 89
663 - 61 - 88
63 + 422 + 49
42 + 781 + 121
84 + 343 - 89
Dear family and whānau,
This week we have been investigating several different ways of approaching addition and subtraction problems. With your child, decide on a problem involving 3 or 4 digit numbers and solve it together, asking your child if they can show you more than one way it can be worked out. Share your thinking as well and compare your strategies.
Put some problems in a container and play Clever Draw: each person draws out a problem, solves it in their head, using materials or with written working out and then has to show the other person how they worked it out using a diagram (a drawing of your thinking).