Comparing ratios with a common whole
Purpose
The purpose of this activity is to support students in recognising that expressing part-whole relationships in ratios is useful for comparing the characteristics of the ratios, such as taste, colour, density, and so on.
Achievement Objectives
NA3-1: Use a range of additive and simple multiplicative strategies with whole numbers, fractions, decimals, and percentages.
NA3-5: Know fractions and percentages in everyday use.
Required Resource Materials
- Connecting cubes
- Calculators
Activity
- Pose a ratio comparison problem, using coloured cubes, where the total number of cubes in each ratio is the same.
Here are the ratios 2:3 and 3:2.
Which mixture has the strongest taste of blueberry?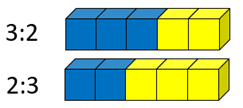
Expressing the part to whole relationships as fractions confirms the result that 3:2 has a stronger blueberry taste than 2:3.
- Pose further examples with common numbers of cubes given in the whole. Ask students to find the part-whole fractions for each ratio and use the fractions to compare the ratios for strength of blueberry flavour. Good examples might be:
Here are the ratios 4:8 and 3:9.
Which mixture has the strongest taste of blueberry?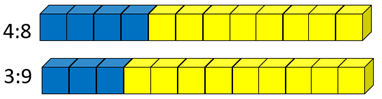

- Here are the ratios 7:3 and 5:5.
Which mixture has the strongest taste of blueberry?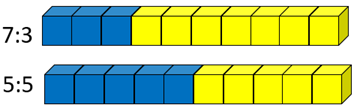

- Here are the ratios 5:4 and 7:2.
Which mixture has the strongest taste of blueberry? - Here are the ratios 4:3 and 2:5.
Which mixture has the strongest taste of blueberry?
- Revisit each ratio above and ask this question:
Which ratio has the strongest taste of apple?
Look for students to recognise that a stronger taste of blueberry corresponds to a weaker taste of apple, whilst a weaker taste of blueberry corresponds to a stronger taste of apple.
- For example, consider the ratios 4:3 and 2:5 above. The part-whole fractions for blueberry are 4/7 and 2/7 respectively.
If we know the fractions for blueberry are 4/7 and 2/7, what are the fractions for apple?
Do students recognise that the fractions for a given ratio add to one (the whole)?
Since 4/7 + 3/7 = 1, if four sevenths of the mixture is blueberry then three sevenths are apple.
Since 2/7 + 5/7 = 1, if two sevenths of the mixture is blueberry then five sevenths are apple.
Next steps
- Progress from making cube models of ratios to working with the symbols. You might fold back to the physical model if answers need verification or if you want students to demonstrate their result from using symbols.
- For example, Recipe A has a 3:5 mix of blueberry to apple, and Recipe B has a 6:2 ratio. Which recipe tastes most strongly of blueberry?
- Use examples where the ratios do not have the same number of parts, but one ratio can be altered to allow comparison.
- For example, which ratio 2:3 or 3:7, has the strongest taste of blueberry?
- Since 2:3 can be copied twice to make 4:6 with the same strength of blueberry, 2:3 has a stronger blueberry taste compared to 3:7.