Equivalent fractions in simple ratios
Purpose
The purpose of this activity is to support students in recognising when part-whole fractions in two or more ratios are equivalent. In this context, equivalence means the same relationship of two measures, such as the relationship of blueberry to apple juice in a mixture.
Achievement Objectives
NA3-1: Use a range of additive and simple multiplicative strategies with whole numbers, fractions, decimals, and percentages.
NA3-5: Know fractions and percentages in everyday use.
Required Resource Materials
- Connecting cubes
Activity
- Introduce this problem.
Here are two mixtures of blueberry and apple juice.
Which mixture tastes most strongly of blueberry?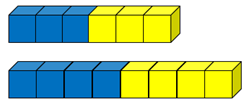
Students should notice that both mixtures are one half blueberry and one half apple. Therefore, both mixtures should have the same taste.
Percentages are one way to compare the mixtures. Both mixtures have 50% blueberry and 50% apple.
- What fractions can you see in the mixtures?
How can we write the mixtures as ratios?
What patterns do you see?
Record students' ideas in an organised way.
Ideally students will notice that 3/6 and 4/8 are equivalent fractions to one half. They may generalise that all fractions equal to one half have a denominator that is twice the numerator. You might record the equivalent fractions as equalities: 1/2 = 3/6 = 4/8.
You might introduce relevant te reo Māori kupu such as hautau ōrite (equivalent fraction).
- What other mixtures will have the same taste?
Construct several possible mixtures and record the ratios and part-whole fractions.
For example, 5:5 is 5/10 blueberry and 5/10 apple.
- Pose a more difficult comparison problem.
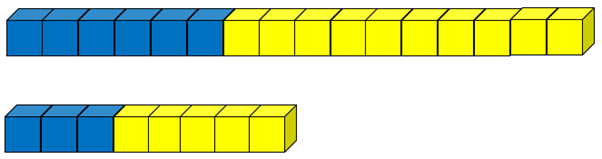
Here are two mixtures of blueberry and apple juice. Which mixture will taste most strongly of blueberry?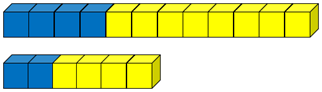
Students should notice that both mixtures are one third blueberry and two thirds apple. Therefore, both mixtures should have the same taste.
- Record the ratios and fractions in an organised way, and record the equivalent fractions as equalities: 4/12 = 2/6 and 8/12 = 4/6.
What patterns do you notice?
Students should recognise the halving of the numerator and denominator across the equals sign. They might also see that the denominator is three times the numerator in 4/12 and 4/12.
- Follow a similar procedure using other mixtures. Good examples are:
- 6:4 and 3:2 (tenths and fifths)
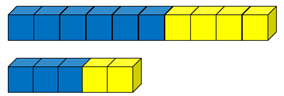
- 1:3 and 2:6 (quarters and eighths)
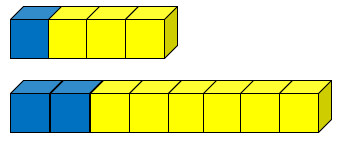
- 6:10 and 3:5 (sixteenths and eighths)
- 6:4 and 3:2 (tenths and fifths)
Next steps
- Increase the level of abstraction by progressing from using cube models to working with the symbols alone. Fold back to materials if needed. For example:
Are these ratios of "blapple" (blueberry apple) juice the same flavour? 3:4 and 9:12
Explain why.
- Progress to comparing mixtures that have different ratios, where the relative strength of flavour can be determined using equivalence. For example, use the ratios 3:3 and 5:4. Since 3:3 represents one half blueberry, an equivalent ratio is 5:5. Since 5:4 contains less apple juice than 5:5 it must have a stronger blueberry taste than 3:3. Similarly compare 2:3 with 4:7 or 3:8 with 2:6.