Identifying fractions in simple ratios
Purpose
The purpose of this activity is to support students in understanding the meaning of part-whole fractions in simple ratios.
Achievement Objectives
NA3-1: Use a range of additive and simple multiplicative strategies with whole numbers, fractions, decimals, and percentages.
NA3-5: Know fractions and percentages in everyday use.
Required Resource Materials
- Connecting cubes
Activity
Show students this ratio made with cubes. You might use the "blapple" juice context (mixture of blueberry and apple juice) or another context that is more relevant to your students.
How can we record this mixture as a ratio of blue to yellow? (2:4 or 1:2)
What fraction of the mixture is blue? (2/6 or 1/3)
What fraction of the mixture is yellow? (4/6 or 1/3)

Note that renaming 2/6 as 1/3 and 4/6 as 2/3 involves unitising the parts in different ways, as shown in the image below.
- If we wanted to make the mixture taste more strongly of blueberry, what could we do?
What fractions would we create?
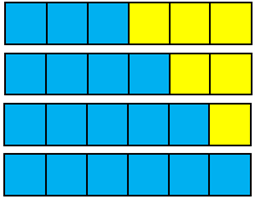
Students are likely to suggest two approaches:- Swapping out a yellow cube for a blue cube. That produces these fractions of blue: 3/6 or 1/2, 2/4 or 2/3, 5/6, 6/6.
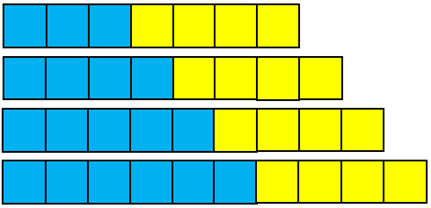
- Adding one cube of blue on each time. That produces the fractions 3/7, 4/8 (1/2), 5/9, 6/10 (3/5), and so on.
- Swapping out a yellow cube for a blue cube. That produces these fractions of blue: 3/6 or 1/2, 2/4 or 2/3, 5/6, 6/6.
- Pose similar problems to see if students can identify the part-whole fractions involved. Increase the strength of the "flavour" of one component to represent different fractions. This variation also supports students to anticipate if one fraction is greater than another, e.g. 4/8 > 3/7. Use inequalities to represent the relationships.
Use beginning ratios including:- 4:6 or 2:3

- 2:6 or 1:3

- 3:5

- 4:6 or 2:3
Next steps
- Increase the level of abstraction by progressing from using cubes as physical models to using only symbols. Instead of making 4:6, ask students to visualise the cube model and name the fractions, 4/10 and 6/10 or 2/5 and 3/5. Explore the "strength of flavour" of a component by adding or subtracting cubes from a model. Such as:
- Begin with a ratio, like 5:5.

Will the flavour change if I…?- Add one blue and one yellow
- Take away a yellow.
- Add a blue.