Unit fraction of a unit fraction
Purpose
The purpose of this activity is to extend students' understanding of fractions as operators to include finding a fraction of a fraction.
Achievement Objectives
NA3-1: Use a range of additive and simple multiplicative strategies with whole numbers, fractions, decimals, and percentages.
NA3-5: Know fractions and percentages in everyday use.
Required Resource Materials
- Sheets of paper (A4 sized is ideal)
- Pens (highlighters if possible or felts)
Activity
- Take a rectangular sheet of paper and follow the steps described below.
- Fold the paper in half lengthways and shade one half with a highlighter pen.
- Fold the paper in thirds widthways and highlight one third of one half.
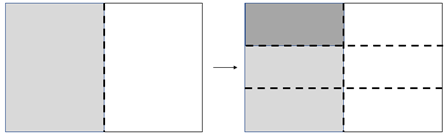
- Reflect on the folding process.
What fraction of the whole rectangle is double shaded? Explain how you know.
Record, describe, and reflect on the relevant expression: 1/3 x 1/2 = 1/6, “one third of one half equals one sixth.”
Explain what this equation means.
What patterns do you see in the numbers? Why do we end up with six equal parts?
- Provide further examples that require students to use paper folding to find a unit fraction of a unit fraction. Allow students to work in groupings that will encourage peer scaffolding and extension. Some students might benefit from working independently, whilst others might need further support from the teacher. Good examples are shown below:
- One quarter of one half. (1/4 x 1/2 = 1/8)
- One third of one third (1/3 x 1/3 = 1/9)
- One half of one fifth. (1/2 x 1/5 = 1/10)
- One third of one quarter (1/3 x 1/4 = 1/12).
- Use paper folding and shading to explore the commutative property of multiplication with fractions.
Does folding in thirds lengthways, then in quarters widthways, give the same result as folding in quarters lengthways, and then in thirds widthways?
Record, describe, and reflect on the relevant expressions. For example: 1/3 x 1/4 = 1/4, “one third of one quarter equals one twelfth.”
Emphasise that while the dimensions of the results are different, both area models show double shaded areas that are one twelfth in size. This illustrates that 1/4 x 1/3 = 1/3 x 1/4.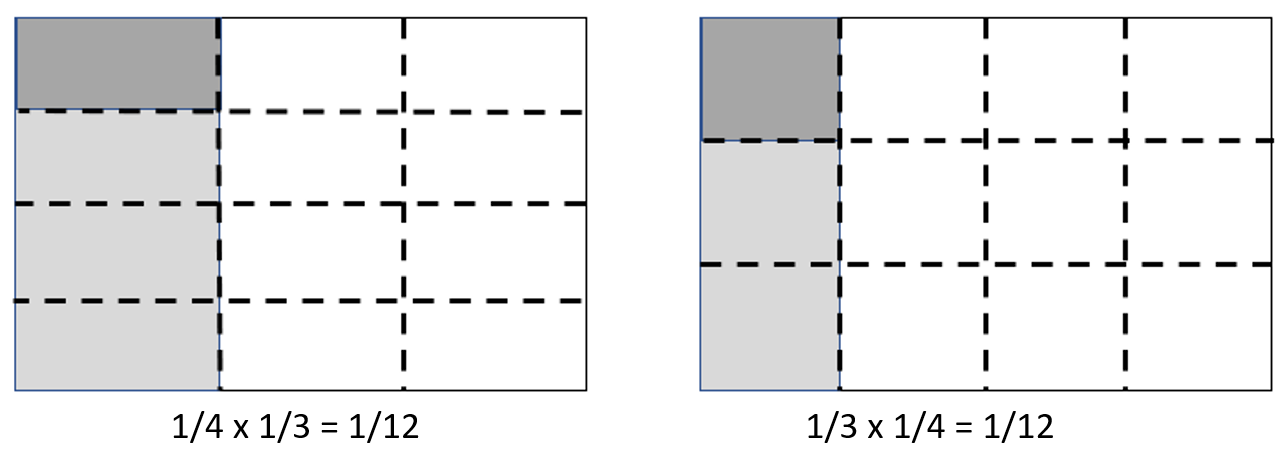
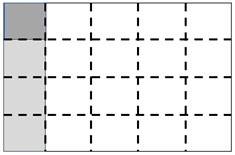
- Provide examples for students to solve, without the support of paper folding and shading. This might begin with drawing diagrams to show the product of two unit fractions. For example, 1/4 x 1/5 = 1/20 might be drawn as:
- Progress to solving problems with equations only, such as those shown below. Provide paper folding for the examples if students have difficulty.
- 1/3 x 1/5 = [ ]
- 1/4 x 1/4 = [ ]
- 1/5 x 1/8 = [ ]
- 1/3 x 1/8 = [ ]
Next steps for further learning
- Encourage students to use a full range of basic multiplication facts with examples such as 1/8 x 1/9 = [ ].
- Use written expressions to formally generalise the multiplication of two unit fractions:
What is the answer to 1/◊ x 1/∆? (In general the product is always 1/◊ x ∆.
- Compare the products of unit fractions. Use examples like: Carla cuts her cake into fifths of quarters. Lucy cuts her cake into sevenths of thirds. The cakes are the same size. Who gives you the bigger piece, Carla, or Lucy?