Non unit fractions as operator
Purpose
The purpose of this activity is to support students understanding that non-unit fractions can operate on whole numbers, for example, 3/4 x 20. Anticipating the result in this way involves finding the unit fraction of the set then multiplying the result by the numerator of the fraction.
Achievement Objectives
NA3-1: Use a range of additive and simple multiplicative strategies with whole numbers, fractions, decimals, and percentages.
NA3-5: Know fractions and percentages in everyday use.
Required Resource Materials
- Counters, tiles, or cubes
- Paper, and pens.
Activity
- Ask students to create a set of 20 objects (counters, tiles, etc.). Consider setting this in a real-life, relevant context.
You are going to get three quarters of your set of counters.
How many counters will you get?
Due to 10 + 10 = 20 and 5 + 5 = 10 being accessible doubles facts, students are likely to anticipate the answer easily. If not, distribute the counters equally on a large area model showing quarters, and explicitly model taking three quarters of the set.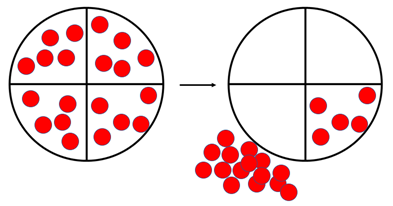
Model how to record the operation as an equation, and connect each symbol to its meaning: 3/4 x 20 = 15
What does 3/4 refer to? (The fraction of the set you received)
What does 20 refer to? (The whole set)
What does 15 refer to? (The result of finding 3/4 of 20)
What does the x symbol mean? (‘of’ as in 3/4 of 20)
What does the = symbol mean? (‘the same’ as in 3/4 of 20 is the same number as 15).
- Ask students to reflect on the two steps in the calculation.
What did we do first? (Find 1/4 of 20 by dividing 20 by four)
What did we do next? (Multiply 1/4 by three to get 3/4)
- Pose similar problems about finding three quarters of different numbers of counters and extend the process to simple examples that involve other non-unit fractions. The aim is for students to:
- Anticipate the result without needing to physically distribute the set.
- Recognise and follow the two necessary steps: dividing the set by the denominator, then multiplying by the numerator.
- Independently record the equations and demonstrate understanding of the meaning of symbols.
- Good examples are shown below. Consider what groupings will be most appropriate for your students. Whilst some may benefit from tuakana-teina relationships in structured peer groups, others are likely to be ready to work independently. Some students may also benefit from further teacher support. Consider also the different means of action and expression (e.g. verbal, written, digital, physical) that your students might use to demonstrate their thinking.
- Start with a set of 12. You get three quarters of the set. (3/4 x 12 = 9)
- Start with a set of 30. You get two thirds of the set. (2/3 x 30 = 20)
- Start with a set of 25. You get four fifths of the set. (4/5 x 25 = 20)
- Start with a set of 100. You get three quarters of the set. (3/4 x 100 = 75)
- Start with a set of 16. You get five eighths of the set. (5/8 x 16 = 10)
- Start with a set of 15. You get two thirds of the set. (2/3 x 15 = 10)
Next steps
- Increase the level of abstraction by progressing from a physical model of equally distribution, followed by multiplication of the numerator, to using multiplication and division basic facts knowledge to anticipate the result.
- Encourage students to use one result to get another. For example:
- If three quarters of 20 equals 15 (3/4 x 20 = 15) what is three quarters of 24?
- If two thirds of 15 equals 10 (2/3 x 15 = 10) what is two thirds of 18 or 21?
- If four fifths of 25 equals 20 (4/5 x 25 = 20) what is three fifths of 25?
- If three quarters of 100 equals 75 (3/4 x 100 = 75) what is three quarters of 96?
- If five eighths of 16 equals 10 (5/8 x 16 = 10) what is six eighths of 16?
- Explore simple equivalence with operators, such as If 1/2 of 24 equals 12, what are 2/4 and 4/8 of 24?
- Reinforce the idea of fractions that are equivalent to one by posing problems such as “what is four quarters of 40?” (4/4 x 40 = 40).