Half as an operator
The purpose of this activity is to support students understanding that multiplication can be applied to find fractions of a whole number. We begin with the simplest fraction, one half.
- Counters, tiles or cubes, paper, and pens.
Ask students to create a set of eight objects (counters, tiles, etc.).
You are going to get one half of your set of counters. How many counters will you get?
Due to 4 + 4 = 8 being an accessible doubles fact, students are likely to anticipate the answer easily. If not, distribute the counters equally on a large area model for one half.
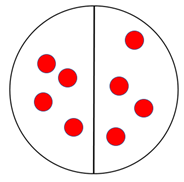
- Model how to record the operation as an equation, and connect each symbol to its meaning:
1/2 x 8 = 4. You might also introduce relevant te reo Māori kupu, such as whakarea (multiply, multiplication) and whakawehe (divide, division).
What does 1/2 refer to? (The fraction of the set you received)
What does 8 refer to? (The whole set)
What does 4 refer to? (The result of finding 1/2 of 8)
What does the x symbol mean? (‘of’ as in 1/2 of 8)
What does the = symbol mean? (‘the same’ as in 1/2 of 8 is the same number as 4).
- Pose similar halving problems about finding one half of different numbers of counters. The aim is for students to develop:
- Anticipation of the result without the need for physically distributing the set.
- More use of division by two to calculate answers.
- Independent recording of the equations with understanding of the meaning of symbols.
Good examples are:
You are going to get one half of your set of counters.
How many counters will you get?
- Start with a set of 18.
- Start with a set of 30.
- Start with a set of 24.
- Start with a set of 100.
- Start with a set of 50.
- Start with a set of 48.
Allow students to work in groupings that will encourage peer scaffolding and extension. Some students might benefit from working independently, whilst others might need further support from the teacher. Consider also the different means of action and expression (e.g. verbal, written, digital, physical) that your students might use to demonstrate their thinking.
Next steps
- Increase the level of abstraction by progressing from using a physical model of equally distributing the set into two parts, to using number knowledge to anticipate the result.
- Encourage students to use one result to get another. For example:
- If one half of 10 equals 5 (1/2 x 10 = 5) what is one half of 14?
- If one half of 20 equals 10 (1/2 x 20 = 10) what is one half of 14?
- If one half of 30 equals 15 (1/2 x 30 = 15) what is one half of 32?
- If one half of 100 equals 50 (1/2 x 100 = 50) what is one half of 106?
- If one half of 50 equals 25 (1/2 x 50 = 25) what is one half of 46?