Getting Started
The purpose of this session is to explore the range of strategies already used by students to solve addition and subtraction problems. This lesson will enable you to evaluate which strategies need to be focused on in greater depth. In turn, you will identify students in your group as "expert" in particular strategies. There are two problems given as examples for exploration. You may want to use further examples of your own. Consider adapting the contexts used in these problems to further engage your students.
- Problem 1: Sarah has $288 in the bank. She then deposits her pay for $127 from her part time job at a cafe. How much does she have now?
Ask the students to work out the answer in their heads or by recording in some way. Give the students plenty of thinking and recording time. Ask the students to share their solutions and how they solved the problem with a peer. The following are possible responses:
Place value (mentally, possibly with the support of equations on an empty number line):
288 + 127 is just like 288 + 100 +20 +7. So that’s 388… 408… 415.
Tidy numbers (mentally, possibly with the support of equations on an empty number line):
If I tidy 288 to 300 it would be easier. To do that I need to add 12 to 288, which means I have to take 12 off the 127. So that’s 300 plus 115.
Algorithm (usually written):
Students may visualise or record a written algorithm like this:
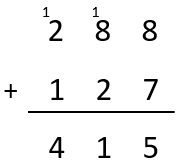
Understanding is revealed by the language used to describe the strategy, such as, “8 plus 7 equals 15. I wrote 5 in the ones place and carried the extra ten into the tens place because 15 is made up of 5 and 10 and I can only record one digit in the ones place.”
As different strategies arise ask the students to explain why they chose to solve the problem in that way. Accept all the correct strategies that are elicited, recording the strategies to reflect upon later in the unit on the class T chart (under the addition heading). You might also ask students to model how their strategies work with place value materials. Note that folding back to justify a strategy is often more difficult than performing the strategy.
- Problem 2 Sarah has $466 in her bank account and spends $178 on a concert ticket. How much money does she have left in her bank account?
Ask students to solve the problem mentally, giving them plenty of thinking and recording time. Then ask students to share their solutions and how they solved the problem with a peer. Possible responses are:
Reversibility (adding on to find the difference with recording to ease memory load):
$466 - $178 is the same as saying how much do you need to add to $178 to get $466. $178 plus $22 makes $200, plus $200 more makes $400 plus $66 makes $466. If you add up $22 plus $200 plus $66 you get $288.
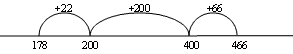
Subtracting a tidy number then compensating
$466 - $200 = $266. I took off $200 instead of $178 so I need to ‘pay back’ $22. $266 + $22 = $288.
Equal additions:
You round the $178 to $200 by adding $22. $466 - $200 is $266. Then you put on $22 to keep the difference the same, so it’s $288.
Algorithm (usually written):
Students may visualise or record a written algorithm like this:
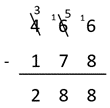
Understanding is revealed by the language used to describe the strategy, such as, “6 minus 8 doesn’t work (ignoring integers) so I changed one ten from the tens column into ones to make 16. I wrote 16 in the ones place and took one ten off in the tens place…”
As different strategies arise, ask the students to explain why they chose to solve the problem in that way. Accept all the correct strategies that are elicited, and justified, recording the strategies to reflect upon later in the unit (under the ‘subtraction’ heading on the class T chart). You might also ask students to model how their strategies work with place value materials. Note that folding back to justify a strategy is often more difficult than performing the strategy.
Subtraction strategies tend to be more difficult to control than addition strategies, given comparable numbers. Look out for students compensating the wrong way (taking more off) in the tidy number strategy and making errors when using the algorithm.
Use your observations to plan for your subsequent teaching from the exploring section outlined below.
Exploring
Over the next two to three days, explore different strategies for addition and subtraction of whole numbers. Give the strategies a name so students can tell others which strategy they are preferencing for a given problem. Highlight when certain strategies are most efficient, for example, In the problem 357 + 189 tidy numbers would be a useful strategy because 189 is close to 200.
Follow a similar lesson structure each day to the introductory session, with students sharing their solutions to the initial questions and discussing why these questions lend themselves to the strategy being explicitly taught. Conclude each session by asking students to make statements about when the strategy would be most useful and why the certain problem is appropriate, e.g., tidy numbers when one number is close to 100 or 1000, standard place value (hundreds, tens, and ones) when no renaming is needed and reversibility when neither of the other two numbers are easy for subtraction. It is important to record examples of strategies as they will be used for reflection at the end of the unit. Some strategies may require more teaching time, greater use of materials, and more scaffolded and individualised teaching. Ensure that students who demonstrate proficiency with the strategies early on in each session have adequate opportunities for practice, extension, and supporting their peers (if appropriate).
The questions provided are intended as examples for the promotion of the identified strategies. If the students are not secure with a strategy you may need to make up some of your own questions to address student needs. Consider adapting the contexts reflected in these problems to further engage your students.
Tidy numbers then compensating
- Room 9 are selling muesli bars at lunchtime to raise money for their camp. They had 434 at the beginning of lunchtime and sold 179, how many did they have left to sell?
The tidy numbers strategy involves rounding a number in a question to make the question easier to solve. In the above question, 179 can be rounded to either 180 (by adding 1), or 200 (by adding 21). If 200 is subtracted (434 – 200 = 234) then the result is 21 less than the answer. 234 + 21 = 255. An empty number line shows this strategy clearly:
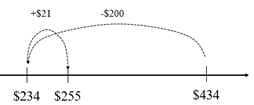
For addition questions, one addend can be tidied by taking from the other addend. Alternatively, both addends might be tidied, and compensation used to adjust for the tidying. - The following questions can be used to elicit discussion about the strategy.
- What tidy number could you use that is close to one of the numbers in the problem?
- What do you need to do to the other number if you tidy up this number? Why?
- Why is this strategy useful for this problem?
- What knowledge helps you to solve a problem like this?
- If the students do not understand the tidy numbers concept, use place value equipment (place value blocks, place value people, beaNZ) and/or an empty number line to model the problems physically. Students should be encouraged to record equations and number lines to track their thinking and reduce load on working memory.
- Use the following questions for further practice if required:
- Ariana has scored 739 runs for her cricket club this season. Last season she scored 294, how many did she score in total in the last two seasons?
Shifting six between the addends gives 739 + 294 = 733 + 300 = 1033. - Nigel sold his guitar for $587 and his amp for $395. How much money did he make from both sales?
Rounding 587 to 600 and 395 to 400, then compensating gives 587 + 395 = 600 + 400 – 13 – 5 = $982. - Farmer Samsoni has 1623 sheep, and he sells 898 sheep at the local sale. How many sheep does he have left?
Rounding 898 to 900 gives 1623 – 898 = 1623 – 900 + 2 = 725 - Other examples might be:
568 + 392
661 - 393
1287 + 589
1432 - 596
- Note that the problems posed here are using a tidying up strategy rather than tidying down i.e. 103 down to 100 as in these situations place value tends to be a more useful strategy.
Place Value (written algorithm)
- For the community hangi, 356 potatoes are peeled and there are 233 left to be peeled. How many potatoes will there be altogether?
The place value strategy involves adding the ones, tens, hundreds, and so on. In the above problem:
300 + 200 is added
Then 50 + 30
And finally 6 + 3
As an algorithm the calculation is represented as:
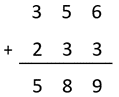
- The following questions can be used to elicit discussion about the strategy:
- How can you use your knowledge of place value to solve this problem?
- Why is this strategy useful for this problem?
- If the students do not understand the strategy, use place value equipment to show the problems physically. Students will find it useful to record and keep track of their thinking .
- Use the following questions for further practice if required:
- Zac has $498 available on his eftpos card and spends $243 on a new BMX bike, how much money does he have left?
- Other problems might be:
3221 + 348
4886 - 1654
613 + 372
784 – 473
Reversibility (adding one rather than subtracting to find the difference)
- Faloa is helping his Mum build a path. There were 438 bricks in the pile and they used 169 of them yesterday. How many bricks have they got left to lay today?
The reversibility strategy involves turning a subtraction problem into an addition one so the problem above becomes:
169 + ? = 438
Using tidy numbers to solve the problem makes calculation easier:
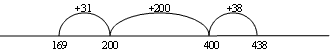
Or
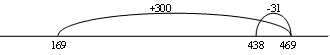
- The following questions can be used to elicit discussion about the strategy:
- How could we think of this as an addition equation?
- What do you need to add to make it easier to solve?
- How can you keep track of how much you have added altogether?
- Why is this strategy useful for this problem?
- What knowledge helps you to solve a problem like this?
- If the students do not understand the concept, use a number line to show the problems graphically. Students will find it useful to record and keep track of their thinking using a number line.
- Use the following questions for further practice if required:
- At the mail sorting office there were 547 letters to be sorted, 268 of these were distributed to private boxes, how many were left to be delivered?
- The school library has a total collection of 1034 books and 459 are issued at the moment, how many are on the shelves?
- Other problems might be:
628 - 342
537 - 261
742 - 353
1521 - 754
1762 - 968
1656 - 867
Reflecting
As a conclusion to the week’s work, give the students the following five problems to solve. Pose the problems in contexts that are relevant and engaging for your students. Ask students to discuss, with a peer or in small groups, which strategy they think will be most useful for each problem and justify their view. For some problems many strategies may be equally efficient. After students have solved the problems, engage in discussion about the effectiveness of their selected strategies.
Some students may have a favourite strategy that they use, sometimes to the exclusion of all others. The best approach is to pose problems where the preferred strategy may not be the most efficient. For example, 289 + 748 is most suited to using tidy numbers and compensation.
Problems for discussion
1318 - 747
763 - 194
433 + 452
1993 + 639
4729 - 1318
You might also like to also try some problems with more than two numbers in them, such as:
721 – 373 - 89
663 - 61 - 88
63 + 422 + 49
42 + 781 + 121
84 + 343 - 89
- Discuss the different strategies explored during the week and ask students to explain in their own words what types of problem each strategy would be useful for solving, and what types of problem each strategy would not be useful for solving. Ask the students to draw a strategy ‘from a hat’ and write questions specific to that strategy for a partner.
- Conclude the unit by showing the students the questions asked in the initial session again. Discuss whether they would solve the problems in a different way now, and how their thinking has evolved. With a partner, students could create a short presentation demonstrating how they would solve one addition and one subtraction problem, naming the strategies used, and justifying the use of their chosen strategies.
Addition and Subtraction Pick n Mix
In this unit we look at a range of strategies for solving addition and subtraction problems with whole numbers. This supports students anticipating, from the structure of a problem, which strategies might be best suited to solving it.
Students at Level 3 of the New Zealand Curriculum select from a broad range of strategies to solve addition problems. This involves partitoning and recombining numbers to simplify problems and draws on students' knowledge of addition and subtraction facts, and knowledge of place value of whole numbers to at least 1000.
The key teaching point is that some problems can be easier to solve in certain ways. Teachers should elicit strategy discussion around problems to get students to justify their decisions about strategy selection in terms of the usefulness of the strategy for the problem. The following ideas support this decision making:
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
The three main types of addition and subtraction problem are applied in this unit: joining sets (addition), separating sets (subtraction), and finding differences (either addition or subtraction). Choose contexts that make links to other relevant curriculum areas, reflect the cultural backgrounds, identities and interests of your student, and might broaden students’ views of when mathematics is applied. Commonly used settings might involve money, points in sport or cultural pursuits, measurements, and collectable items. For consistency, you could choose one context in which all of the problems presented within this unit could be framed.
Te reo Māori kupu such as tāpiri (addition), tango (subtraction), and huatango (difference in subtraction) could be introduced in this unit and used throughout other mathematical learning
Getting Started
The purpose of this session is to explore the range of strategies already used by students to solve addition and subtraction problems. This lesson will enable you to evaluate which strategies need to be focused on in greater depth. In turn, you will identify students in your group as "expert" in particular strategies. There are two problems given as examples for exploration. You may want to use further examples of your own. Consider adapting the contexts used in these problems to further engage your students.
Ask the students to work out the answer in their heads or by recording in some way. Give the students plenty of thinking and recording time. Ask the students to share their solutions and how they solved the problem with a peer. The following are possible responses:
Place value (mentally, possibly with the support of equations on an empty number line):
288 + 127 is just like 288 + 100 +20 +7. So that’s 388… 408… 415.
Tidy numbers (mentally, possibly with the support of equations on an empty number line):
If I tidy 288 to 300 it would be easier. To do that I need to add 12 to 288, which means I have to take 12 off the 127. So that’s 300 plus 115.
Algorithm (usually written):
Students may visualise or record a written algorithm like this:
Understanding is revealed by the language used to describe the strategy, such as, “8 plus 7 equals 15. I wrote 5 in the ones place and carried the extra ten into the tens place because 15 is made up of 5 and 10 and I can only record one digit in the ones place.”
As different strategies arise ask the students to explain why they chose to solve the problem in that way. Accept all the correct strategies that are elicited, recording the strategies to reflect upon later in the unit on the class T chart (under the addition heading). You might also ask students to model how their strategies work with place value materials. Note that folding back to justify a strategy is often more difficult than performing the strategy.
Ask students to solve the problem mentally, giving them plenty of thinking and recording time. Then ask students to share their solutions and how they solved the problem with a peer. Possible responses are:
Reversibility (adding on to find the difference with recording to ease memory load):
$466 - $178 is the same as saying how much do you need to add to $178 to get $466. $178 plus $22 makes $200, plus $200 more makes $400 plus $66 makes $466. If you add up $22 plus $200 plus $66 you get $288.
Subtracting a tidy number then compensating
$466 - $200 = $266. I took off $200 instead of $178 so I need to ‘pay back’ $22. $266 + $22 = $288.
Equal additions:
You round the $178 to $200 by adding $22. $466 - $200 is $266. Then you put on $22 to keep the difference the same, so it’s $288.
Algorithm (usually written):
Students may visualise or record a written algorithm like this:
Understanding is revealed by the language used to describe the strategy, such as, “6 minus 8 doesn’t work (ignoring integers) so I changed one ten from the tens column into ones to make 16. I wrote 16 in the ones place and took one ten off in the tens place…”
As different strategies arise, ask the students to explain why they chose to solve the problem in that way. Accept all the correct strategies that are elicited, and justified, recording the strategies to reflect upon later in the unit (under the ‘subtraction’ heading on the class T chart). You might also ask students to model how their strategies work with place value materials. Note that folding back to justify a strategy is often more difficult than performing the strategy.
Subtraction strategies tend to be more difficult to control than addition strategies, given comparable numbers. Look out for students compensating the wrong way (taking more off) in the tidy number strategy and making errors when using the algorithm.
Use your observations to plan for your subsequent teaching from the exploring section outlined below.
Exploring
Over the next two to three days, explore different strategies for addition and subtraction of whole numbers. Give the strategies a name so students can tell others which strategy they are preferencing for a given problem. Highlight when certain strategies are most efficient, for example, In the problem 357 + 189 tidy numbers would be a useful strategy because 189 is close to 200.
Follow a similar lesson structure each day to the introductory session, with students sharing their solutions to the initial questions and discussing why these questions lend themselves to the strategy being explicitly taught. Conclude each session by asking students to make statements about when the strategy would be most useful and why the certain problem is appropriate, e.g., tidy numbers when one number is close to 100 or 1000, standard place value (hundreds, tens, and ones) when no renaming is needed and reversibility when neither of the other two numbers are easy for subtraction. It is important to record examples of strategies as they will be used for reflection at the end of the unit. Some strategies may require more teaching time, greater use of materials, and more scaffolded and individualised teaching. Ensure that students who demonstrate proficiency with the strategies early on in each session have adequate opportunities for practice, extension, and supporting their peers (if appropriate).
The questions provided are intended as examples for the promotion of the identified strategies. If the students are not secure with a strategy you may need to make up some of your own questions to address student needs. Consider adapting the contexts reflected in these problems to further engage your students.
Tidy numbers then compensating
The tidy numbers strategy involves rounding a number in a question to make the question easier to solve. In the above question, 179 can be rounded to either 180 (by adding 1), or 200 (by adding 21). If 200 is subtracted (434 – 200 = 234) then the result is 21 less than the answer. 234 + 21 = 255. An empty number line shows this strategy clearly:
For addition questions, one addend can be tidied by taking from the other addend. Alternatively, both addends might be tidied, and compensation used to adjust for the tidying.
Shifting six between the addends gives 739 + 294 = 733 + 300 = 1033.
Rounding 587 to 600 and 395 to 400, then compensating gives 587 + 395 = 600 + 400 – 13 – 5 = $982.
Rounding 898 to 900 gives 1623 – 898 = 1623 – 900 + 2 = 725
568 + 392
661 - 393
1287 + 589
1432 - 596
Place Value (written algorithm)
The place value strategy involves adding the ones, tens, hundreds, and so on. In the above problem:
300 + 200 is added
Then 50 + 30
And finally 6 + 3
As an algorithm the calculation is represented as:
3221 + 348
4886 - 1654
613 + 372
784 – 473
Reversibility (adding one rather than subtracting to find the difference)
The reversibility strategy involves turning a subtraction problem into an addition one so the problem above becomes:
169 + ? = 438
Using tidy numbers to solve the problem makes calculation easier:
Or
628 - 342
537 - 261
742 - 353
1521 - 754
1762 - 968
1656 - 867
Reflecting
As a conclusion to the week’s work, give the students the following five problems to solve. Pose the problems in contexts that are relevant and engaging for your students. Ask students to discuss, with a peer or in small groups, which strategy they think will be most useful for each problem and justify their view. For some problems many strategies may be equally efficient. After students have solved the problems, engage in discussion about the effectiveness of their selected strategies.
Some students may have a favourite strategy that they use, sometimes to the exclusion of all others. The best approach is to pose problems where the preferred strategy may not be the most efficient. For example, 289 + 748 is most suited to using tidy numbers and compensation.
Problems for discussion
1318 - 747
763 - 194
433 + 452
1993 + 639
4729 - 1318
You might also like to also try some problems with more than two numbers in them, such as:
721 – 373 - 89
663 - 61 - 88
63 + 422 + 49
42 + 781 + 121
84 + 343 - 89
Dear family and whānau,
This week we have been investigating several different ways of approaching addition and subtraction problems. With your child, decide on a problem involving 3 or 4 digit numbers and solve it together, asking your child if they can show you more than one way it can be worked out. Share your thinking as well and compare your strategies.
Put some problems in a container and play Clever Draw: each person draws out a problem, solves it in their head, using materials or with written working out and then has to show the other person how they worked it out using a diagram (a drawing of your thinking).
31 or None
This is a level 3 number and algebra strand activity from the Figure It Out series. It relates to Stage 6 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (174 KB)
use basic facts to solve equations
FIO, Level 2-3, Basic Facts, 31 or None, page 4
At least 2 classmates to play with
Game
This activity is based on an ancient Chinese game in which players had to make given totals by using four single-digit numbers and the four operations. Thirty-one is a good target as there are many ways in which students can reach this score. Students could use a tally sheet to record who has the highest score in each round.
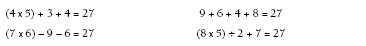
After students have played the game several times, the target number can be changed. Students may wish to describe why it is easier to get a target of 31 than a target of 13. Similarly, they can be given a target total such as 27 and asked to write as many four-digit combinations for it as they can.
For example:
Where students use different types of calculators, particularly scientific and four-function, the issue of order for operations may arise. For example, given 4 + 6 x 3 – 5 = , a scientific calculator will get 17 whereas a four-function calculator will get 25. Four-function calculators perform calculations in the order of keying, that is, 4 + 6 = 10, then 10 x 3 = 30, and then 30 – 5 = 25.
A scientific calculator uses the convention for operations, that is, multiplication and division are calculated before addition and subtraction. With 4 + 6 x 3 – 5 = , the 6 x 3 = 18 is performed first, and then 4 is added and 5 subtracted: 18 + 4 – 5 = 17.
Activity
Students will need to approach this systematically. A table would be useful.
Answers to Activity
Game
Game of addition, subtraction, multiplication, and division
Activity
64 plums
Material Masters Digit Cards 4.1
A Standard Written Form for Addition
Solve addition and subtraction problems using decomposition, leading to a written algorithm.
Number Framework Stage 6
Problem: “Work out 235 + 386 in a standard written method.”
Record the following on the board or modelling book and discuss the reason for every step.
Examples: 234 + 478 459 + 328 308 + 536 889 + 67 ...
Using Imaging
Problem: “Find 235 + 487 by a standard written method.
Use a compact form
Discuss how five and seven produce two ones and one 10 and 12 tens produce two tens and one hundred.
Examples: 484 + 468, 279 + 326, 508 + 536, 89 + 557, 367 + 902, 78 + 970 ...
Using Number Properties
Examples: Find the answers by using a standard written form: 3 404 + 478, 4 079 + 2 327, 588 + 4 536, 59 + 4 556, 3 268 + 8 902, 78 + 970 ...
People's Ages
Solve problems using a combination of addition, subtraction, multiplication and division mental strategies.
Number Framework Stage 6
Problem: “John is interested in the history of his family. He sees from family recordsthat his great-grandmother was born on 25 October 1879, and she died on 13 December 1945. How old was she when she died?”
Write and discuss why the problem can be written as 1879 + ? = 1945.
Model 1879 and 1945 on an open number line and insert 1900 on the number line. Discuss the solution. “From 1879 to 1900 is 21, and from 1900 to 1945 is 45. So great grandmother was 21 + 45 = 66 years old when she died.” Record this on the board or modelling book.
Problem: “Jonah Rogers was born on 12/03/1823 and died on 14/09/1891. How old was he when he died?”
Discuss why 1891 – 1823 is a suitable calculation to make, which reduces to finding 91 – 23. Record the answer on the board or modelling book.
Examples: “How long did these people live?” Record the answers on the board or modelling book.
Born Died
21/09/1853 17/11/1901
13/11/1937 01/12/1980
01/03/1899 12/12/1987
28/04/1848 01/05/1924
30/08/1888 1/09/1923
23/05/1902 21/07/1933
Problem: “On a tour of England, Malcolm Smith finds the gravestone of one of hisancestors, which reads “Joseph Smith. Born 22nd July 1638. Died 12th April 1665.”
How old was Joseph when he died?”
Discuss why 1665 – 1638 = 27 produces an answer that is one too large (because 12th April precedes 22nd July). So Joseph was 26 when he died. Challenging examples:
“How long did these people live?” Record the answers on the board or modelling book.
Born Died
21/12/1943 12/01/2003
13/12/1956 01/12/1991
01/03/1856 12/12/1911
28/09/1924 12/01/2002
30/08/1878 21/03/1922
23/12/1919 21/07/1991
Human Pyramids
This is a level 3 number activity from the Figure It Out series. It relates to Stage 6 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (218 KB)
use mental strategies to solve problems involing addition, subtraction, multiplication, and division
A calculator
Activity One
As with those for page 11, this activity provides opportunities for the mathematical processes achievement objectives listed above. You may decide to select one or two of them for particular attention.
These activities use an unusual context to encourage problem solving that involves the four operations. Warn students not to attempt to build a pyramid with their classmates because of the dangers involved.
The pyramid structure implies that the mass of each person is distributed equally onto the two people below. As some people have two people above them, they have half of each of those people’s mass as well a share of any mass that has been placed on those above them.
Todd gets half of 46.5 kilograms. Vince gets half of 44.5 kilograms. Sue gets the same as Todd and Vince combined.
Activity Two
Suggest to students that they use the same mass for each person in their pyramid model and they keep it a simple number. This way, they have a better chance of seeing how much the halving effect reduces the mass that each person on the bottom row has to support. They can also see that the end people have less mass to support than the middle people.
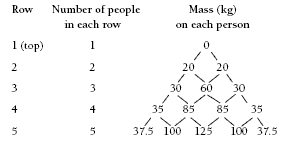
For example, what would happen if every person weighed 40 kilograms and you used 15 people?
Look at the bottom row. The end people each still have less than one person’s mass to support. The second person in has 2.5 times the mass of one person. The middle person has the most to support, and it is just over the mass of three people, even though there are 10 people above that person.
Answers to Activities
Activity One
1. 14.5 kg
2. Todd 23.25 kg, Sue 45.5 kg, Vince 22.25 kg
3. Jo none, Sue and Tina 14.5 kg, Rua 27.25 kg, Kim 52.5 kg, Vince 25.25 kg, Henry 35.625 kg, Andrew 75.875 kg, Matt 70.375 kg, Barbara 30.125 kg
Activity Two
a. Answers will vary.
b. Answers will vary.
c. The middle person supports the most mass (just over the mass of 3 people), the next 2 support about 2.5 times the mass of 1 person, and the end people support less than the weight of 1 person.