Properties of operations
In this unit students work out their own generalisations of the properties of number operations through their exploration of addition, subtraction, multiplication and division.
- Consolidate understanding of simple properties of addition, subtraction, multiplication and division.
- Discover and use some more complex properties of addition, subtraction, multiplication and division.
Patterns are used in the curriculum for several reasons: to develop facility with numbers and calculations, to work on generalisations, and to explore the properties of number operations (which is the focus of this unit). It is important to develop a strong arithmetic basis for interpreting algebraic expressions. This enables students to carry out algebraic manipulations with understanding. For example, the distributive law:
(a + b) x c = a x c + b x c
The distributive law is used constantly in algebraic manipulation, and is a formal statement of a property of addition and multiplication. It states that adding two numbers and then multiplying the answer by 3 (for instance), gives the same answer as if both the numbers were first multiplied by three and then added together. Similarly, students already intuitively know the algebraic equivalence below:
a - (b + 1) = (a - b) – 1
This can be seen in situations such as “if I take 101 away from a number, I get one less than if I take 100 away from it”. At this level, the properties are not expressed with letters, but are illustrated with examples, as the intention is to build up a strong intuition for how the four operations behave.
The questions in this unit are present in algorithm form. However, you should value and build on whatever strategies your students are confident using to add, subtract, divide, and mutiply whole numbers.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
- varying the type of questions asked and the numbers involved (higher or lower) to vary the complexity
- sharing visuals to demonstrate the problems
- providing equipment to support their learning.
- grouping students in flexible groups to support and extend students
- checking and drawing on students’ prior knowledge
- using digital tools to model concepts and demonstrate learning
- providing sentence starters for general statements.
The context for this unit can be adapted to suit the interests and experiences of your students. For example, you might use the context of native animals or native marine life for the problems. Consider how you might make links to a context that is relevant to the learning interests and cultural backgrounds of your students, or to learning from another curriculum area.
Te reo Māori vocabulary terms such as tāpiri (addition), tango (subtraction), whakarea (multiplication), and whakawehe (division) and the te reo Māori words for numbers could be used in this unit and throughout other mathematical learning.
Session 1: Biscuits
Here the students try to find general rules relating to a subtraction problem disguised as a problem involving eating biscuits. Reframe the context of this problem as appropriate.
- A family bought a packet of 20 biscuits and they ate 6. There were 14 left. 20 – 6 = 14. Illustrate this by using
 for remaining biscuits and
for remaining biscuits and  for eaten biscuits.
for eaten biscuits.
When you know that 20 – 6 = 14, what other subtractions do you immediately know the answer to?
It might be useful to construct a table of students’ suggestions that may include:
| Suggestions | Illustrations | Equation |
| 20 – 6 = 14 | ||
| If they ate one more, there would be one fewer left |  | 20 – 7 = 13 |
| If they ate two more, there would be two fewer left |  | 20 – 8 = 12 |
| If they ate one fewer, there would be one more left |  | 20 – 5 = 15 |
| If they had 5 more to start with, but ate the same number, there would be 5 more left | 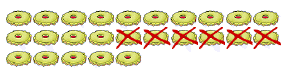 | (20 + 5) – 6 = 14 + 5 = 19 |
| If they had 5 more to start with, and ate 5 more, there would be the same number left | .gif) | (20 + 5) – (6 + 5) = 14 |
| If they had bought twice as many and eaten twice as many, there would be twice as many left | 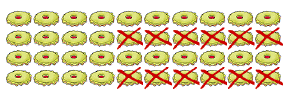 | (2 x 20) – (2 x 6) = (2 x 14) |
| If they had bought half as many and eaten half as many, there would be half as many left |  | Half of 20 – half of 6 = half of 14 |
- Discuss students’ suggestions and get them to illustrate why their idea works using the diagram (or models) of the biscuits.
- Some of the students’ suggestions will be true only for the actual numbers involved. They will not demonstrate general properties of subtraction. Someone may, for example, suggest that if the family ate four more biscuits, there would only be ten left. Draw attention to general properties, where possible, that will hold for all numbers of biscuits. For instance, all of the suggestions in the table above are general. This is because the verbal statements would apply to any number of biscuits you care to choose for the initial subtraction. General statements can be tested by trying other numbers of biscuits and seeing if the verbal statement still holds true.
- Summarise the general properties and test them on other numbers.
Session 2: Subtraction
In this session, students explore and test properties of subtraction.
Ask a student to come and write a complicated subtraction on the board and work out the answer. For example:
.gif)
Ask students to suggest other subtractions they can now do easily, using this answer. They might suggest that the top line can be increased (e.g. by 1, 2, 100, 1000, see below), or decreased (e.g. by 30, see below) giving corresponding increases and decreases in the answers. Such examples can be done mentally and checked with a calculator or written algorithm.
.gif)
- Ask the students to explain the reason behind this property of subtraction with reference to another relevant context such as buying sports equipment worth $473 from a bank account containing $2358.
- Ask students to explain, in their own words, why increasing (or decreasing) the number subtracted causes the answer to be decreased (or increased) by the same amount.
- Ask the students to explain the reason behind this property of subtraction, with reference to a simple context.
Ask the students to suggest other things that we can easily work out using the answer to this subtraction and to explain their reasoning.
Examples: if both numbers are increased by the same amount, the answer is not changed, if both numbers are doubled or halved, the answer would be doubled, if both are multiplied by ten, the answer is multiplied by ten.
- Students can now choose their own complicated subtraction, work it out and make up some other subtractions that they can now easily do. Support students as necessary and allow them to check their solutions with a calculator. Then they write down the ten favourite subtractions that they have found and explain how they knew they would be correct.
Session 3: Multiplication
This session follows the same steps as the above session on subtraction, with a stronger emphasis on checking a variety of numerical examples.
- Both relationships that work and relationships that do not work should be discussed. For example, if one number is multiplied by ten, then the answer is multiplied by ten. However, if one number is increased by ten, then the answer is not (usually!) increased by ten
- Test proposed relationships on a variety of easy numbers e.g. to test proposal that “ if I double one number and have the other, the product remains the same” check: 10 x 6 = 60, 20 x 3 = 60, 5 x 12 = 60 and 4 x 5 = 20 and 2 x 10 = 20 and 8 x 2.5 = 20.
- Calculators can be used to check harder examples too.
Session 4: Division
This session follows exactly the same steps as the above sessions on subtraction and multiplication.
Session 5: Addition and consolidation
Here the students work by themselves on addition problems. This session is an attempt to bring together the ideas of the previous sessions.
- Remind the class what has been done in the last four sessions. Ask them to work with another member of the class but this time concentrate on addition. Remind them that they have to guess a rule and then check it.
- Get the various groups to report back to the class.
What did you find?
Why did it work?
Will it always work? - Recall the different things that worked for the four operations.
Are there any rules that are the same?
Are there any rules that are different? - Get the class to summarise what they have found on a poster. Display the posters.
Dear parents and whānau,
Today in maths we worked out these questions for you to do. See how quickly you can do them. Can you see any patterns?
.gif)