I'm So Sorry I Ate Chocolate
This unit explores the magnitudes of sides and angles of a triangle and leads to the discovery and proof of the Sine Rule. This Rule is then used to solve triangles, some of which arise in practical situations. Finally we compare the use of the Sine Rule and the Cosine Rule.
Note that this unit may contain more material than you need for some classes. You may want to choose only some of the sessions if you have not planned to allot five sessions on the Sine Rule and its relation to the Cosine Rule.
- solve triangles using the Sine Rule
- understand what a conjecture is
- solve triangles using the Cosine Rule
- know when it is appropriate to use the Sine Rule and when to use the Cosine Rule
It’s probably a good idea right at the start to say what the title of this unit is all about. As you are well aware you can apply the Sine Rule to find an unknown length in a triangle when you have two angles and one side. What’s more you can apply the Cosine Rule to find an unknown length when you have two sides and the included angle. This is essentially the difference between them. So we have One Side: Sine Rule; and One Angle: Cosine Rule. Or 1 Side Sine and 1 Angle Cosine. It might help students to remember that if they remember I(1)’m S(ide)o S(ine)orry I(1) A(ngle)te C(osine)hocolate. But then again, maybe not!
By now you will realise that this unit concentrates on the Sine Rule and its application to solving triangles, that is, to finding the unknown sides and angles of triangles. First we discover and prove the Sine Rule and then we use it in theoretical and practical situations. Finally we use both the Sine and Cosine Rules to find unknown angles and sides in a triangle. In the process we discover which Rule fits which situations best.
Note that Cosine Rule, Level 6 is a unit on the Cosine Rule. We will assume in this unit that students have already met and used the Cosine Rule.
It may be that there is too much material here for your Level 6 class. If your time is limited, you may want to choose from what is offered. To help you decide which sessions you might want to do we list the content of the sessions and which sessions fit together.
Sessions 1 and 2 involve the discovery and proof of the Sine Rule.
Session 3 involves solving triangles with some of the problems being word problems.
Session 4 involves a practical task.
Session 5 compares the use of the Sine and Cosine Rules.
Hopefully there are one or two new ideas that you can use either at this level or later.
At this point it is worth mentioning that practical skills are required in some internal Achievement Standards in the NCEA. It may be worthwhile to start teaching some of these skills at Level 5.
It is perhaps worth noting that many of the things that might be considered as ‘extras’ here, such as the use of the words ‘conjecture’ and ‘generalisation’, are concepts that are important in mathematics generally and should be used by students both here and elsewhere.
Prerequisites
In order to be able to do this unit, students will need to know:
- how to construct triangles accurately using rulers, compasses, and protractors
- how to find the values of the sine, cosine and tangent of angles
- how to find the sides of right angled triangles using sine, cosine and tangent
- how to use the Cosine Rule
Compasses
Rulers
Protractors
Copymaster 1 and answers
Copymaster 2 and answers
Session 1
In this session we start to discover the Sine Rule by trying to extend the situation that holds in right angled triangles.
Teachers’ Notes
As we do in the Cosine Rule, we first pose a problem that the students should not yet know how to solve. Here the problem does not include a right angle, so we can’t use sine, cosine, or tangent in a straightforward way; and it does not contain two sides and the included angle, so the Cosine Rule cannot be used. Here is the problem.
Find the unknown side in the triangle below.
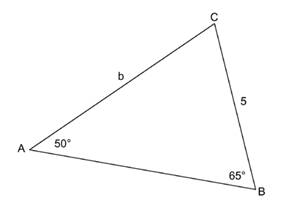
To start down the road to discovering the Sine Rule, we first look at the situation in a right angled triangle and see if there is anything there that can be extended. This leads us to doing some experiments with a series of triangles that keep as much as possible fixed so that we can guess how the variables are related. So here goes.
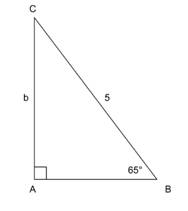
If we were given the problem above, then we would know that b = 5 sin 65º, and we could quickly calculate b. But is this likely to work in the original problem? Insert the perpendicular shown. This will equal 5 sin 65º but it should be easy to see that this is smaller than the side b that we are after.
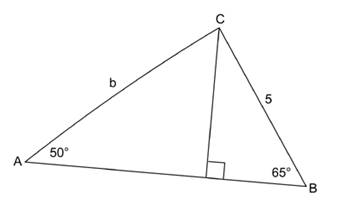
What do we do now? Perhaps it is worth checking, in a few examples, by how much b actually differs from 5 sin 65º. We can construct the following diagram and measure the various ‘b’ sides.
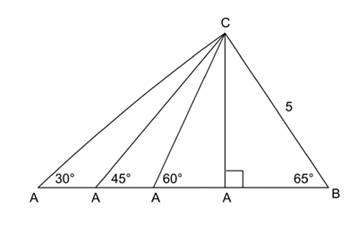
Using the measurements from the diagram we can complete the ‘b measured’ column in the table below. In what way(s) are 5 sin 65º and ‘b measured’ related? From this we can guess various possibilities for the correction.
|
angle |
5 sin 65º |
b measured |
correction |
comments |
|
30º |
4.53 |
|
|
|
|
45º |
4.53 |
|
|
|
|
60º |
4.53 |
|
|
|
|
90º |
4.53 |
4.53? |
none |
|
These should lead to an embryonic Sine Rule:
|
5 sin 65º = b sin A |
or
|
|
where B is one of 30º, 45º, 60º, or 90º.
You might then conjecture that this relation is independent of the two values 5 and 65º. Can you find evidence that the following conjecture is true?
|
|
where A is the angle opposite to the side of length a and B is the angle opposite B.
Teaching Sequence
-
Introduce the problem in the Teachers’ Notes. Discuss how this might be solved and end with the conclusion that we need a new idea.
-
Show that the use of sine does not work and think about how you might set up an experiment to see how far off of the sine value ‘b’ is.
-
In groups, let the students complete the table of the Teachers’ Notes by constructing and measuring the sides in the diagram above the table.
What is the correction factor?
What conjecture can you make about what is happening? -
Discuss the results that have been obtained and see that they fit the conjecture(s) being made. Suggest that more evidence may need to be collected to test any conjectures.
What evidence should you collect?
Session 2
Here we find more evidence for the Sine Rule conjecture and prove it.
Teachers’ Notes
It will be worth trying a couple more practical measuring experiences for several values of A that will enable tables to be drawn up to substantiate the Sine Rule conjecture of the last session. The table that is used in this session can confidently use the columns below.
For B = 70º:
|
Angle A |
b/sin B |
5/sin A |
columns equal? |
|
30º |
|
|
|
|
45º |
|
|
|
|
60º |
|
|
|
|
90º |
|
|
|
The conjecture then can be extended to the following, where a, b, c are the sides of any triangle and A, B, C are the angles opposite those sides.
|
|
Proving the Sine Rule is not quite as complicated as proving the Cosine Rule. Look at the diagram below.
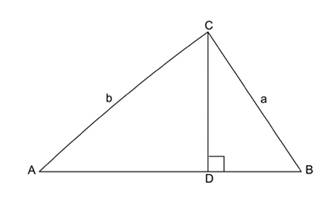
From triangle ADC, CD = b sin A.
On the other hand, from triangle BCD, CD = a sin B.
So b sin A = a sin B.
This can be rearranged to give
|
|
By dropping a perpendicular from B to AC, it can be shown that
|
|
From there the conjecture above follows.
Teaching Sequence
-
Continuing on from the last session and using the Teachers’ Notes as a guide, discuss with the class how they might find further evidence for their conjecture(s).
-
Send them away in groups of two to work on the kind of data collection suggested in the Teachers’ Notes. Go from group to group to check that they are going in the right direction, answer any questions that they have, and make sure that they are not making errors.
-
Bring the class together to see how they feel abut the conjecture(s) now.
-
Lead them through a proof that a/sin A = b/sin B. Then get them to see if they can follow your model to obtain a/sin A = c/sin C.
-
Ask them if they can now solve the original problem from session 1.
-
Give them time to make notes on the Sine Rule, its proof, and how it can be used to solve triangles.
Session 3
This session provides the chance to use the Sine Rule to solve triangles. Some of the problems here are word problems.
Teachers’ Notes
In this session the students get a chance to practice their recently acquired knowledge on the problems of Copymaster 1 . These contain both ordinary questions and word problems. Some of these problems are quite testing. If there are not enough straightforward problems for you it is not difficult to make up more questions like the first two or you can find them in books.
You might start this session by solving the problem at the beginning of the Teachers’ Notes in Session 1.
Teaching Sequence
-
Start this session by reminding students how the problem from session 1 was solved using the Sine Rule. Get them to talk about how they might solve any triangle where they were given one side and two angles.
-
How would you solve a triangle like this?
-
The remainder of this session is essentially a practice session where students solve the problems in copymaster 1. They might work in pairs at first. When you think that they are on top of the method, suggest that they work by themselves.
-
Bring the class together to discuss any difficulties. For students who work faster than the others, ask them to make up a problem of their own that can be solved using the Sine Rule. Try to give these problems to others to solve.
Session 4
This is a practical session where we use the Sine Rule in the school grounds.
Teachers’ Notes
In this session we see how to find the height of an inaccessible object using the Sine Rule. We have provided one suggestion that might be a bit complicated. For a simpler practical measuring task you might modify Question 3(iii) of copymaster 2.
Look for something in the school grounds that is reasonably high but the foot of which is inaccessible. The highest point of one of the buildings might be appropriate. The diagram below shows you what needs to be measured. C is the inaccessible ‘foot’ and CD is the height that we want to find. Under the diagram we show what calculations need to be made.
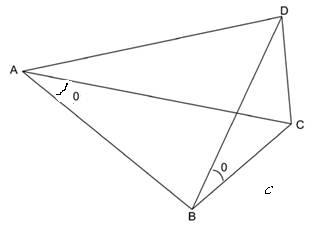
If we can measure c, and angles A and B, then we can find angle C because angles A, B, and C add up to 180º. Now we can find CB using the Sine Rule.
CB = c sin A/sin C.
Now triangle BCD is a right angled triangle. So
CD = CB tan θ.
Hence ![]()
Since we can measure each of c, A, C and θ, we can find CD, the inaccessible height.
Before taking the class out into the school grounds to do their measuring, you should talk about the accuracy of their measurements and to what accuracy you would expect them to be able to find CD. You should also talk about the method of calculating CD so that they will know why they are measuring the length c and the three angles.
This is also a good opportunity to get some practice in estimating lengths and angles. If practical, it will help the calculations when using the above equation if c = 10 metres or some other ‘simple’ length. How long is 10 metres? Can the students estimate it before they measure it precisely? How accurate are their guesses?
What about the angles A, C and θ? How good are the students at guessing these values?
Teaching Sequence
-
In this session the students are to do a practical task in the school grounds. Prepare them by talking them through the exercise, getting them to think about what they need to measure, how they can measure it, how accurate they need to be, and what maths they will need to use.
-
This task will require at least two students to work together because of the practical difficulties of the measuring instruments. To avoid groups getting in each other’s way, the lengths c that they measure should vary in magnitude and position. As a check it might be a good idea for groups to measure their variables more than once.
-
When the measurements have been taken, return to the class and let the groups calculate CD. Move round the class and give assistance where needed.
-
Compare the different values that the students got. Are the results all sufficiently close (to within measuring error) or have some serious errors crept in?
-
Allow time for the students to make notes on the task that they have carried out.
Session 5
In this final session we compare the use of the Sine and Cosine Rules and try to see in which situations it is preferable to use the Sine Rule and in which the Cosine Rule is best.
Teachers’ Notes
From the form of the Sine Rule we can see that if we know two angles and a side that is opposite one of the angles, then we can find the side opposite the other angle.
So with 1 Side (you can use) Sine.
|
I Side Sine – I’m So Sorry. |
Of course if you know two angles of a triangle, you can deduce the third. So in fact if you know two angles and a side you can find any and all of the other two sides using the Sine Rule.
At this point you may need to remind them about the Cosine Rule. Here if you know two sides and an angle you can find the other side. If the side you want is opposite the known angle, then just a straight application of the Cosine Rule will get you home. Otherwise you may have to solve a quadratic equation (or use the Sine Rule with an angle as the unknown).
Recall then that with 1 Angle (you can use) Cosine.
|
I Angle Cosine – I Ate Chocolate. |
Copymaster 2 gives a variety of problems where the students have to decide whether it is best to use the Sine Rule or the Cosine Rule. The mnemonic
I’m So Sorry, I Ate Chocolate
may help them to remember which Rule is best in which situation.
It might be worth mentioning Question 2(iv) of Copymster 2 this point. This could be a good question for your bright students to work on. The point is that there are no triangles with A = 71º, a = 15 and c = 20. The diagram below shows what the problem is. The point is that a line going from A at an angle of 71º will not intersect with a circle of radius 15 with centre at B.
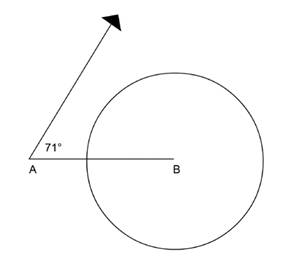
If we keep angle A at 71º, the circle that will just hit the ray from A will be the one to which the ray is a tangent. This circle will have radius 20 sin 71º = 18.91. Any circle with radius larger than 18.91 will also hit the ray and so form a triangle. 18.91 is therefore the smallest value of a that will give us a triangle and we will get aq triangle for a > 18.91.
On the other hand, if we keep a = 15, then we can reduce the angle of 71º at A till we eventually get a triangle. The first time that this happens is when the ray is tangent to the circle with radius 15. The length of b when this happens is given by sin A = 15/20, so A = 48.59º. Further, any angle A such that 0º < A < 48.59º will produce a triangle. 48.59º is therefore the largest value of A that will give us a triangle.
Teaching Sequence
-
Recall the Sine and Cosine Rules.
-
In some random order discuss two triangles where either the Sine Rule or the Cosine Rule might be used.
What are the essential differences between the two Rules?
When can we use Sine Rule and when the Cosine Rule?
You might suggest the mnemonic: I’m So Sorry I Ate Chocolate. -
Now send them to work on Copymster 2 where there is a mixed bag of problems, some of which require the Sine Rule and some the Cosine Rule.
-
Move from group to group offering assistance and asking leading questions.
-
Discuss the problems at the end of the class.
-
Let the students make notes on what they have done.
-
Provide some time for the students to make notes on the work of this session.
-
From time to time in the future, ask them what the Sine/Cosine Rule is; when to apply the Sine/Cosine Rule; what the mnemonic is.