Down on the farm
The unit is designed as a simple introduction to systems of linear equations. Students solve problems in which they meet two constraints to find a single solution. Both constraints can be expressed as linear equations.
- Identify and find values for variables in context.
- Identify linear relationships in context.
- Represent linear relationships using tables, graphs and simple linear equations.
- Draw strip diagrams to represent linear equations and ratios.
- Solve problems in which two or more conditions must be met.
Systems of equations are extremely useful for modelling real world situations. Often two or more conditions exist in a situation that must be satisfied. We can often express conditions using representations such as tables, graphs and equations. These representations provide powerful tools for solving problems.
As an example, consider simultaneously meeting these two conditions:
- There are twice as many chickens as pigs.
- The number of pigs and chickens equals 90.
Condition (i) can be represented by the following table, graph and equation.
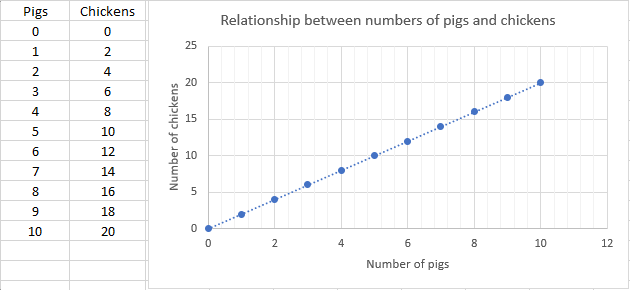
c = 2p or p = c/2 where p represents the number of pigs and c the number of chickens.
Condition (ii) can be represented in the same ways.
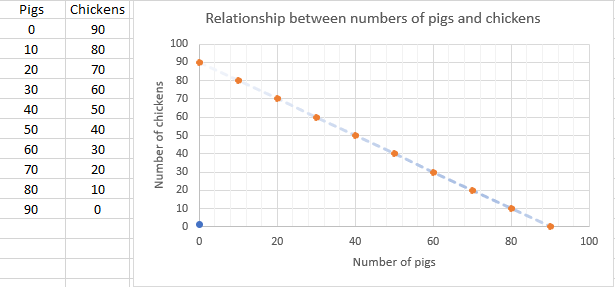
c + p = 90 or c = 90 – p or p = 90 – c
Satisfying both conditions involves finding values for the number of pigs and number of chickens that work. In table form this involves searching for a common pair in both tables. In graph form this involves finding an intersection of both lines.
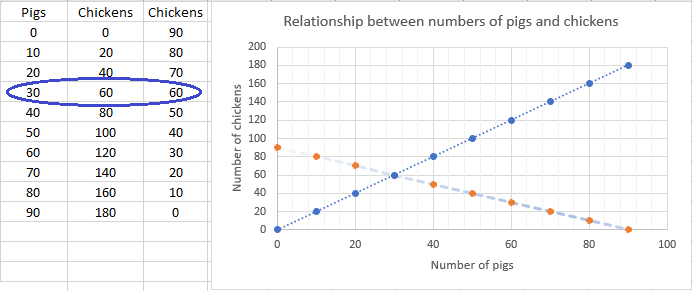
An algebraic method is to solve the two equations simultaneously. There are different ways to do this. Here is a substitution method:
- 2p = c
- c + p = 90
Putting 2p in for c in equation (ii) gives:
2p + p = 90 so 3p = 90 and p = 30.
Since c + p = 90, c must equal 60.
The problems in this unit involve using representations to meet common conditions.
Specific Teaching Points
Representing relations in algebraic equations involves two important and connected types of knowledge, related to the language conventions (semiotics), and to the nature of variables. When we write c = 2p, or c = 90 – p + 2 the equations are meaningless to anyone else unless we clearly define what the variables, c and p, represent. Note that both c and p refer to quantities that vary and are not fixed objects, such as a chicken or a pig. Quantities are a combination of count and measurement unit. In this case c expresses many animals. Animals are the unit in this problem. 2p means the number of pigs multiplied by two, not twenty-something.
Semiotics, the meaning of symbols and signs, is central to algebra. Transfer between semiotic forms is difficult at times. For example, a statement such as “there are twice as many chickens and pigs” seems innocuous and it is easy to generate a table of values that satisfy the statement. However, recording the statement as an algebraic equation requires a student to accept letters as variables, not as objects that can be counted. 2p = c or c = 2p is correct but appears ordinally different to the spoken form. Some spoken languages are more consistent with algebra and would express the relation as “To get the number of chickens multiply the number of pigs by two.”
Working with variables also requires acceptance of lack of closure, that is thinking with symbols (c and p in this case) without specifically knowing the values they hold. For example, knowing that c = 2p can be substituted into c + p = 90 while conserving its structure, irrespective of whatever the value of c or p, is itself a generalisation.
The equals sign represents a statement of ‘transitive balance’ meaning that the balance is conserved if equivalent operations are performed on both sides of the equation. Knowledge of which operations conserve equality and those which disrupt it are important generalisations about the properties of numbers under those operations, e.g. distributive property of multiplication.
Students can be supported through the learning opportunities in this unit by differentiating the nature and complexity of the tasks, and by adapting the contexts. Ways to support students include:
- providing a physical or diagrammatic model, e.g. cubes or counters or icons, so students can experiment with the conditions in the problems
- modelling how to record relationships as tables of values, graphs, and equations. Videos of modelling these representations are included in the resources
- explicitly telling students about the conventions of letter symbols, e.g. 5y means five times an unknown y, with a ‘missing’ multiplication sign
- encouraging students to work collaboratively and share their ideas
- encouraging students to check their solutions against the conditions of the problem.
Task can be varied in many ways including:
- altering the complexity of the problems in two ways. Smaller numbers make trial and improvement and physical/diagrammatic strategies viable. Simplifying the conditions makes problems considerably easier. Total conditions, e.g. 12 animals in total, are easiest and ratio conditions are hardest
- allowing access to calculators so students can experiment with possible values without the burden of calculation. However, expect them to anticipate the results of their calculation changes before pressing the keys
- providing or removing examples of a pattern or relationship before trying to generalise the relationship using variables.
The contexts for this unit can be adapted to suit the interests and cultural backgrounds of your students. Animals on the farm provide the contexts for all problems in the unit and appeal to a range of students. Other contexts can also be used, such as buying items at a shop, e.g. socks at $3 per pair and hats at $12 each. Catering at a marae or tulaga fale provides a useful context around managing a budget while still providing ample food for manuhiri (visitors). People in an extended whānau also provides an interesting context, with variables such as the number of adults and children.
Te reo Māori vocabulary terms such as ōrite (equal), kīanga taurangi (algebraic expression), kīanga ōrite (equivalent expression) and whārite rārangi (linear equation) could be introduced in this unit and used throughout other mathematical learning.
Prior Experience
It is anticipated that students at Level 4 and 5 understand, and are proficient with, multiplicative thinking. Students are expected to know about simple ratios though this unit reintroduces some key ideas. Some proficiency at solving linear equations would be beneficial, so working through the units on linear algebra before this unit would be helpful.
Session One
Begin with this new version of a very old problem. The problem solving pathway in e-ako maths includes a version of this problem called "Sheep and chickens". This might be used as an extension task for students who enjoy the algebraic equation approach.
On Mr MacDonald’s farm there are only pigs and chickens. He counts 24 heads and 80 legs. How many of each kind of animal is there? |
After discussing important conditions in the problem, encourage the students to work in small co-operative groups. Allow access to supportive tools such as calculators and computers. Recording on paper will be important.
Look for the following common approaches:
Trial and improvement
This approach typically involves choosing a pair of possible values for the number of pigs and chickens, and making alterations until the other condition is met. For example, 12 pigs and 12 chickens might be tried. This assumption meets the number of heads condition but 4 x 12 + 2 x 12 = 72. So that pair of values fails the number of legs condition. However, systematic adjustment of increasing the number of pigs and reducing the number of chickens will eventually give the answer. Note that this strategy is very protracted if the numbers involved are large.
Figurative diagram
Students using this strategy often begin with numbers of pigs and chickens that satisfy the number of heads condition, though sometimes they draw 48 animals of one kind. Some students draw figures that satisfy the number of legs condition. It is important that the drawings are symbolic and not literal (i.e. not life-like pigs or chickens) for two reasons. Life-like drawings are time consuming and indicate that the farmyard context assumes more importance than the conditions of the problem. A drawing might look like this, with 12 pigs and 12 chickens:
Chickens can easily be turned into pigs by adding two extra legs until a solution is found that meets the number of legs condition.
Making a table
Often students’ approach the problem using trial and error (rather than improvement). They try combinations of pigs and chickens in an unsystematic way. A table helps them to organise their data but also allows for noticing of patterns that otherwise are missed.
An example of a table based strategy is given below:
Number of Pigs | Number of chickens | Number of pigs’ legs | Number of chickens’ legs | Total number of legs | ||
0 | 24 | 0 | 48 | 48 | ||
1 | 23 | 4 | 46 | 50 | ||
2 | 22 | 8 | 44 | 52 | ||
… | … | … | … | … |
The table can be extended until a solution is found. Note that use of a spreadsheet makes this strategy highly efficient.
Equations
This strategy is unusual for students at Level 4 unless they have exposure to writing and solving linear equations (link to first algebra learning object unit). First, students need to identify the variables in this problem. While it makes sense to use p and c as symbols, it is very important that students regard these as variables not fixed objects. P is not a pig nor is c a chicken. P represents possible numbers of pigs and c possible numbers of chickens.
Second, students need to write the conditions using these variables. Conventions are involved here, notably that 4p means 4 x p and 2c means 2 x c, and equals means a state of balance or sameness.
- p + c = 24 (Number of heads condition)
- 4p + 2c = 80 (Number of legs condition)
Third, solving for p or c involves trusting that these variables can remain ‘unclosed’ and conserved under a sequence of steps. This is a significant shift from arithmetic thinking which aims to ‘close’ the answer as immediately as possible.
Equation (i) can be reorganised as p = 24 – c or c = 24 – p. Either of these equalities can be substituted into equation (ii) so the equation is in one variable:
4(24 – c) + 2c = 80 or 4p + 2(24 – p) = 80
Discussion
- After a suitable time, gather the class to discuss their solution strategies. Focus mostly on students’ thinking and on the relative efficiency of their strategies. It is unlikely that either graphical or equation based approaches will occur naturally. Video 1 presents a table and graph based solution, should showing that approach seem worthwhile.
- Ask students to classify the problem.
What kind of problem is this?
You want students to say that the problem involves variables, numbers of pigs and chickens. It also involves two constraints (restrictions) that must both be met for the problem to be solved. - Ask: Think about a similar problem where the numbers are much larger. Which strategy is the best to use? Why?
- Provide the students with Copymaster 1 that contains variations on the original problem. Increasing the difficulty of the problems makes trial and improvement, diagrammatic and table based strategies less viable, and preferences algebraic methods.
Solutions:
The "Sheep and chickens" problem solving e-ako provides guidance to developing a general algebraic solution to the pigs and chicken problem.
Session Two
Introduce the next farmyard problem using slide 2 of the PowerPoint.
On Young Maree MacDonald’s farm the ratio of pigs to sheep to chickens is 2:3:5. Maree has 640 animals in total. How many of each kind of animal are there? |
- Ask: What does a ratio mean?
- Look for students to recognise that the ratio is a comparison of numbers that applies to all the animals on Maree’s farm. So, the ratio might be expressed as “For every two pigs there are three sheep and five chickens.” You might need to refer the students back to the PowerPoint slide to answer some of these questions.
- What fraction of the total number of animals are the chickens? (one half) How do you know? (⁵/₁₀ is equivalent to ¹/₂)
- Is it true that one fifth of the animals are pigs? (Yes. ²/₁₀ = ¹/₅)
- Is it true that the number of chickens is two and one half times the number of pigs? (Yes. 2 ¹/₂ x 2 = 5)
- How many times more chickens are there than sheep? (1 ²/₃ x 3 = 5 because ⁵/₃ x 3 = 5)
- Let the students solve the problem of how many of each animal are on Maree’s farm. Then bring the class together to share strategies. Video 2 shows how a strip diagram might be used to represent the problem. You can pause the video at points when students are posed a question.
- Slide 3 of the PowerPoint provides a variation of Maree’s problem in which the part of the collection of animals is given but not the whole. Ask the students to represent the problem as a strip diagram and solve it. Encourage them to work in small groups.
- Gather the class together to share their solution strategies. Video 3 talks through a solution using strip diagrams.
- Copymaster 2 has a collection of Maree, the farmer, ratio problems for the students to solve. Students might work collaboratively or independently. Look for them to:
- represent the unknowns and unknowns in strip diagrams.
- use the diagrams to identify and calculate missing parts or totals.
- look for common factors in numbers.
Solutions:
Problem One
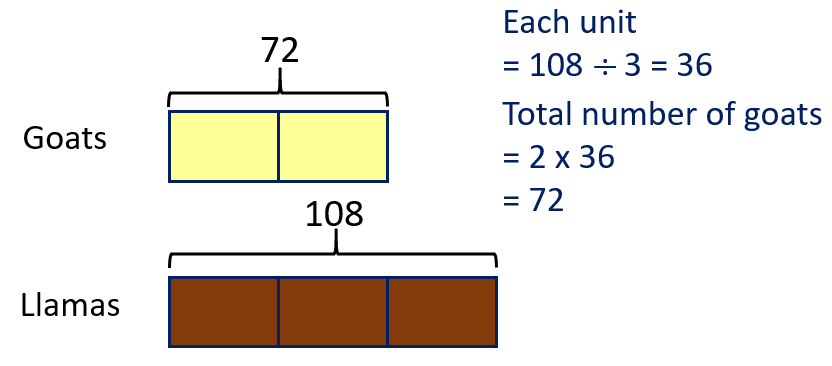
Problem Two
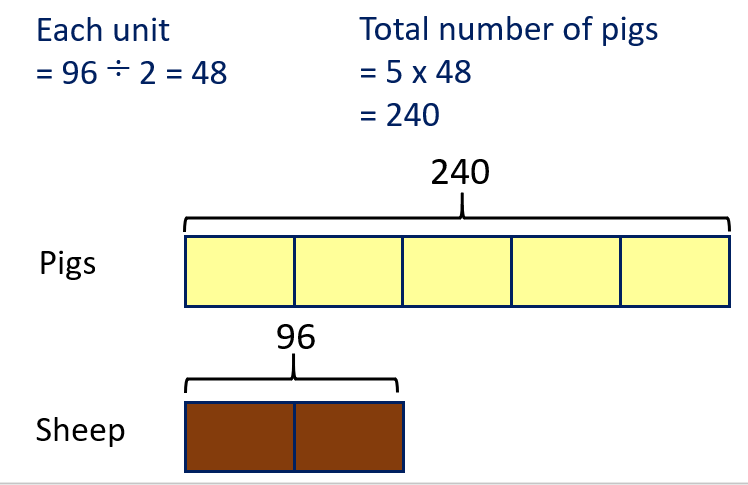
Problem Three
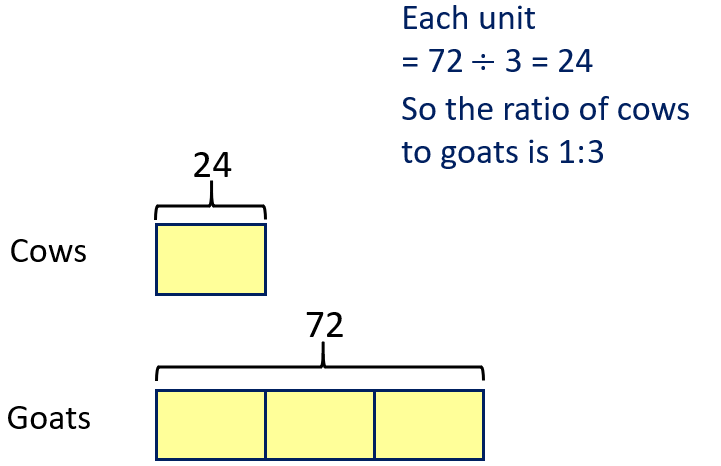
Problem Four
This problem is easier if you think of parts consisting of 12 animals, and the whole made of 45 parts of 12.
Animal | Number | Fraction | ||
Goats | 72 | 6/45 = 2/15 | ||
Llamas | 108 | 9/45 = 1/5 | ||
Pigs | 240 | 24/45 = 4/9 | ||
Sheep | 96 | 8/45 | ||
Cows | 24 | 2/45 |
Session Three
Show the student today’s starting problem on Slide 4 of the PowerPoint. Ask them to identify the important conditions in the problem:
Jessica Jones buys 60 animals at the market. She only buys cows and pigs. Cows are $120 each, three times the price of pigs. The total cost is $4 800. How many of each animal does she buy? |
- Students should recognise that pigs cost $40 each.
- Ask: Can we write the conditions algebraically?
First, the variables need defining. Number of cows might be represented by c or any other letter, and the number of pigs by a different letter, possibly p.
Second, equations can be written for the conditions.
c + p = 60 for the condition of sixty animals. - Ask: How else could this equality be expressed? E.g. c = 60 – p or p = 60 – c
- The second condition of cost is more difficult. Students may offer p = 3c to represent the cost relationship between cows and pigs. This is incorrect in two ways. P and c are used to stand for the number of each animal not the price of cows and pigs. So, the variables have changed. The relationship is incorrect as well. One pair where the price relationship holds is $12 for a cow and $4 for a pig. Putting c = 12 and p = 4 into the incorrect equation p = 3c gives 4 = 3 x 12, which is incorrect.
- Remind the students of the total legs condition from the pigs and chickens problem.
How did we express that condition?
So, 120c + 40p = 4800 represents the cost condition. - Put the students into small co-operative groups to solve the problem. Allow access to tools such as paper and pens, calculators, and computer spreadsheets. As students work, encourage them to look for similarities between Jessica’s problem and the pigs and chicken problems. The same strategies that worked for those problems; trial and improvement, diagrams, tables and algebra; should work on this problem.
- After a suitable time, gather the class to share solutions. Discuss the efficiency of the different methods. Video 4 shows a spreadsheet supported solution but other methods may be equally efficient. Students may reason that if all the animals were cows then $4800 would buy 40 cows. Exchanging one cow for three pigs keeps the cost the same but effectively increases the number of animals by two. So, ten exchanges of one cow for three pigs (a ratio) reduces the cow number to 30 and increases the pigs number to 30, which is the solution.
- The algebraic solution is also accessible, given the students’ experience in Lesson One:
c + p = 60 so p = 60 – c (total number constraint)
120c + 40p = 4800 (cost constraint)
Putting (i) into (ii) gives:
120c + 40(60 – c) = 4800
120c + 2400 – 40c= 4800
80c = 2400
C = 30
The second problem for this lesson is available on Slide 5 of the PowerPoint.
Farmer Fred goes to market. He buys 100 animals for $100. Lambs cost $10 each. Piglets cost $3 each. Chicks cost $0.50 each (50 cents). How many of each animal does he buy? |
- This is an old problem which may explain the cheap prices. It is challenging because there are only two conditions, total number and cost, but there are three unknowns, the numbers of lambs, piglets and chicks. Discuss with the students how they might simplify the search for solutions. Important observations are:
- Lambs are very expensive at $10 each, and their total cost is always a multiple of $10 ($10, $20, $30,…)
- Chicks are the cheapest animals and the number of them must be even since two of them cost a whole dollar.
- Putting those clues together can limit the search.
What is the greatest number of lambs that can be bought?
Ten lambs take up all the cost, nine lambs cost $90 and you can only buy 20 chicks with the remaining $10, eight lambs cost $80 and you can only buy 40 chicks with $20, etc.
By that thinking, the number of lambs that it is possible to buy can only be one, two, three, four or five. That makes the problem easier to solve. - Let the students work at a solution using the strategies they know from previous problems. Look for:
- Do they systematically work through possible solutions for l = 0, 1, 2, 3, 4, 5?
- Do they use diagrams and equations to support their solution finding?
- Do they use spreadsheets and adjust the variables according to the ‘number of lambs’ condition?
- Do they notice when solutions are impossible? For example, fractional or negative numbers of animals are impossible.
- Bring the class together after a suitable time to share progress towards a solution. Students can be sent away again to work in groups even if they have not found the solution after sharing.
The solution is five lambs, one piglet and 94 chicks.
Session Four
In this lesson students are encouraged to connect their strategies and knowledge of ratios to solve problems. Slide 6 of the PowerPoint poses the problem of expressing a ratio as an equation.
The ratio of pigs to sheep is 1:2. If p = number of pigs and s = number of sheep, write an equation for this relationship. |
Before asking for suggestions make a table of possible numbers for p and s:
Number of pigs (p)Number of sheep (s)1210203651071400Students are likely to suggest two equations, s = 2p or p = 2s. Check to see which of the equations works with the table values. An important idea is that p and s refer to numbers of animals not an individual animal, pig or sheep. So, the equation s = 2p works but seems counter-intuitive with the way the ratio is said, “For every pig there are two sheep” or “There are twice as many sheep as pigs.”
- Slides Seven and Eight give two other ratios for the students to write as equations.
The ratio of goats to cows is 1:5. So c = 5g is the equation.
The ratio of horses to llamas is 2:3. So 2l = 3h is the equation. Check by putting trusted pairs of values for h and l into the equation. If h = 20 and l = 30 then the equation predicts 2 x 30 = 3 x 20 which is correct.
In each case creating a table of values helps to verify the correct equation. - Next the students work on Copymaster 3. This worksheet presents several problems in a form where ratio statements provide one of the conditions to satisfy. If students can turn the ratio statements into algebraic equations, they can use the strategies learned previously. The last problem is very difficult and designed for extension.
Solutions:
